Мажоритарное резервирование.

Мажоритарное резервирование – это резервирование методом голосования.

Суть состоит в том, что образуется несколько одинаковых каналов (нечетное число) и в систему вводят восстанавливающий орган – мажоритарный элемент. Восстанавливающий орган сравнивает результаты каналов и выдает результат по большинству.

Мажоритарный элемент может быть построен на логических элементах, либо используются стационарные элементы.

N – число входов (нечетно), обычно на практике 3 или 5.

Рассчитаем вероятность отказа системы при мажоритарном резервировании. Рассмотрим случай с 3-мя однотипными каналами.

– вероятность отказа канала.

Структурная схема надежности:

,

.

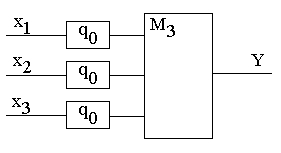
Восстанавливающий элемент находится в основном соединении с каналами. Его отказ приведет к отказу всей системы.

Учитывая, что и , вероятность отказа системы:

.

При резервировании систем данным методом количество элементов, охваченных мажоритарным элементом, может варьироваться, следовательно, меняется надежность системы.

Рассмотрим разбиение мажоритарной системы на узлы таким образом, чтобы обеспечить максимальную надежность резервируемой системы.

Каждая из систем состоит из равнонадежных элементов с .

Для повышения надежности используется мажоритарное резервирование .

Система допускает мажоритарное резервирование от до .

Причем каждый узел резервирования требует одного мажоритарного элемента, находящегося в основном соединении и характеризующегося вероятностью отказа .

Требуется разбить систему на оптимальные узлы резервирования.

Структурная схема надежности для одного узла резервирования будет иметь следующий вид:

Учитывая, что элементы основной системы и резервной находятся между собой в основном соединении и , структурная схема преобразуется к следующему виду:

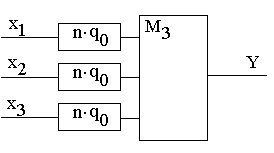
Вероятность отказа системы при мажоритарном резервировании для 3-х каналов имеет вид: .

Для данного случая вероятность отказа узла:

.

Вероятность отказа одного узла с учетом мажоритарного элемента:

.

Количество узлов резервирования: .

Структурная схема надежности всей системы при таком разбиении:

.

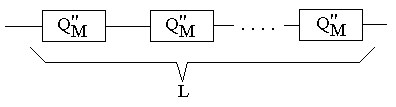
Вероятность отказа всей системы при мажоритарном резервировании:

Найдем минимум.

.

Величина отказа всей системы при оптимальном разбиении:

.

Ненагруженный резерв.

Резервирование замещением.

Если при общем резервировании время наработки на отказ всей системы характеризуется наработкой самой надежной системы, то при резервировании замещением общая наработка на отказ характеризуется суммой наработок на отказ каждой из систем.

При мажоритарном резервировании резервные системы не подключены до тех пор, пока работоспособна основная система. Т.е. можно считать, что в этот момент .

На структурной схеме резервирование замещением обозначается следующим образом:

Рассмотрим резервирование замещением для двух основных участков. Т.е. для нормального участка работы и для участка старения.

Рассмотрим надежность резервирования системы замещением для случая, при котором наработка на отказ основной системы подчинена нормальному закону.

В этом случае: .

Суммарная наработка на отказ равна сумме наработок каждой из систем. А т.к. наработка основной системы подчинена нормальному закону, то в этом случае и суммарная наработка будет также описываться нормальным законом распределения, но с другими параметрами ( ).

Тогда вероятность отказа:

.

Выразим параметры резервированной системы через параметры основной: .

Если все используемые системы идентичны, то можно записать:

.

Дисперсия суммы случайных величин также равна сумме дисперсий этих величин, и для равнонадежных систем:

Таким образом:

.

Если для основной системы выполняется условие , то оно тем более будет выполняться и для резервированной системы, и тогда .

Если же это условие не выполняется, то необходимо произвести проверку этого условия для резервированной системы и рассчитать коэффициент .

Пример.

В системе используется резервирование замещением кратности 3. Среднее время безотказной работы каждой из систем 1000 часов. = 250 часов.

Найти выигрыш в надежности за счет резервирования для наработки 3000 часов.

, , , ,

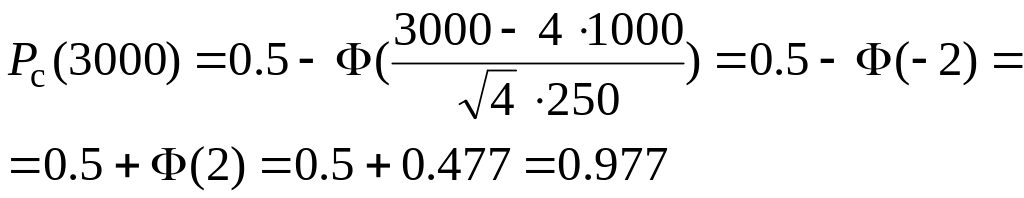
(раз).

Резервирование замещением при экспоненциальном законе.

Будем рассматривать работу системы на нормальном участке эксплуатации.

Пусть основная система состоит из узлов, находящихся в основном соединении.

Тогда: .

Средняя наработка на отказ системы: .

Суммарная наработка на отказ системы будет равна сумме наработок каждой из систем.

, где – кратность резервирования.

Каждая из наработок является случайной величиной, распределенной по экспоненциальному закону.

Известно, что сумма случайных величин, каждая из которых подчиняется экспоненциальному закону с одинаковыми параметрами, будет подчиняться закону распределения Пуассона.

И вероятность отказа:

.

Для удобства расчетов преобразуем это выражение.

При справедливо:

Тогда: .

Подставим в исходную формулу:

.

Итак, окончательно получим:

.

Если , то .

Если , то .

Пример.

В системе используется резервирование замещением кратности .

Интенсивность отказов .

Обеспечить для наработки вероятность безотказной работы системы не хуже 0.9 ( ).

Рассчитать выигрыш в надежности за счет резервирования.

: .

Без резервирования не обеспечивается система с высокой надежностью.

Нужно .

: – не удается достичь требуемой надежности.

: – обеспечили требуемую надежность.

Рассчитаем выигрыш в надежности:

Расчет надежности систем с зависимыми отказами.

Понятие Марковских процессов.

Граф состояний. Классификация состояний.

На практике, как правило, отказ одного из элементов системы влечет за собой изменение режимов работы других.

Расчет надежности таких систем выполняют с использованием теории Марковских процессов. Причем, этот расчет можно произвести только для нормального участка эксплуатации, где .

В этом случае каждое последующее состояние системы будет зависеть от предыдущего (и только от него). И, т.о., рассматривая все возможные состояния системы, можно учесть изменения параметров надежности одних элементов, вызванные отказом других.

Пример. Система энергообеспечения, состоящая из 2-х однотипных генераторов, работающих на общую нагрузку.

Возможные состояния системы:

– оба генератора исправны.

– отказал 1-й генератор, работает 2-й.

– отказал 2-й генератор, работает 1-й.

– отказали оба генератора.

– характеризуют нормальную работу системы.

– отказ системы.

Вероятность безотказной работы системы будет определяться нахождением системы в одном из состояний .

Для удобства или наглядности при расчете систем с использованием понятия состояний используется понятие ориентированного графа состояний.

Ориентированный граф состояний – совокупность вершин, часть из которых соединена отрезками, при этом вершины графа соответствуют состояниям системы. Они изображаются окружностями, внутри которых – соответствующие состояния системы.

Для рассматриваемого выше примера ориентированный граф состояний будет иметь следующий вид:

Стрелки, соединяющие вершины, характеризуют возможность перехода системы из состояния в состояние.

Рассмотрим основные виды состояний, используемые в графе:

1. Состояние называется источником, если система может выйти из этого состояния, а войти в него не может.

2. Состояние называется концевым, если системы может войти в него, а выйти – нет.

3. Состояние называется транзитивным, если система может и войти, и выйти из него.

Множество состояний системы называется эргодическим, если из любого состояния система может попасть в любое состояние , т.е. система не должна содержать источники и поглощающие состояния.

Если система остается в этом же состоянии, то это называется задержкой (на графе рисуется петля).

Дискретная цепь Маркова (Марковский процесс

с дискретным временем и дискретными состояниями).

Пусть имеется система с дискретными состояниями .

Предположим, что случайные переходы системы из состояния в состояние могут происходить только в фиксированные моменты времени.

Моменты переходов будем называть шагами процесса. А время – началом случайного процесса.

На моменты времени , в принципе, никаких ограничений не накладывается, хотя для удобства расчетов: .

После 1-го шага процесса система окажется в одном из своих возможных состояний: .

На k-м шаге: .

Случайный процесс, происходящий в системе, называется Марковским процессом с дискретными состояниями и дискретным временем (дискретная цепь Маркова), если вероятность перехода системы в состояние на (k+1)-м шаге процесса зависит только от того, в каком из состояний система находилась на k-м шаге процесса, и не зависит от того, когда и каким образом она попала в это состояние.

Очевидно, что вероятность перехода системы из состояния в состояние будет характеризоваться условными вероятностями на (k+1)-м шаге, которые называются переходными вероятностями и характеризуют вероятность того, что система на (k+1)-м шаге займет состояние , при условии, что на k-м шаге она была в состоянии :

.

Если вероятности не зависят от шага процесса, то цепь Маркова называется однородной.

И тогда: .

Переходные вероятности удобно записывать в виде матрицы состояний:

.

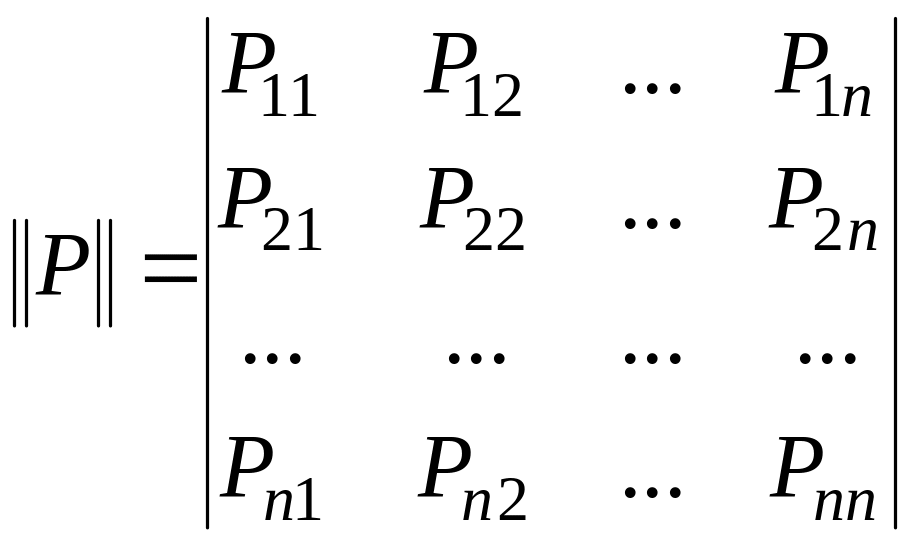Т.к. на каждом шаге состояний система может находиться только в одном из возможных состояний, то для каждой строки переходной матрицы справедливо равенство:

Для расчета безусловных вероятностей пребывания системы в одном из возможных состояний, помимо матрицы переходных состояний, необходимо иметь начальное распределение вероятностей системы:

Для удобства расчета в дискретной Марковской цепи иногда вместо матрицы переходных вероятностей используется размеченные граф состояний, на котором задержки не проставляются, а в матрице состояний они получаются следующим образом: .

Для рассматриваемой системы энергообеспечения размеченный граф состояний будет иметь следующий вид:

Рассчитаем безусловную вероятность нахождения системы в одном из возможных состояний на (k+1)-м шаге.

Пусть в момент времени система находилась в состоянии с вероятностью .

Найдем вероятность того, что на 1-м шаге процесса система перейдет в состояние (т.е. найдем ).

По формуле полной вероятности будем иметь: .

Теперь можно рассчитать вероятности пребывания системы на 2-м шаге:

.

И т.д.

Таким образом:

Пример.

Для рассматриваемой системы энергоснабжения найти распределение вероятностей для первых двух шагов процесса, считая, что оба генератора идентичны и каждый из них имеет интенсивность отказов . При отказе одного из генераторов интенсивность отказов другого возрастает до . Известно, что в момент времени оба генератора были исправны. Считается, что осмотр генераторов производится один раз в сутки.

Осмотр генераторов производится один раз в сутки, следовательно, шаг случайного процесса – 24 часа.

Найдем переходные вероятности системы.

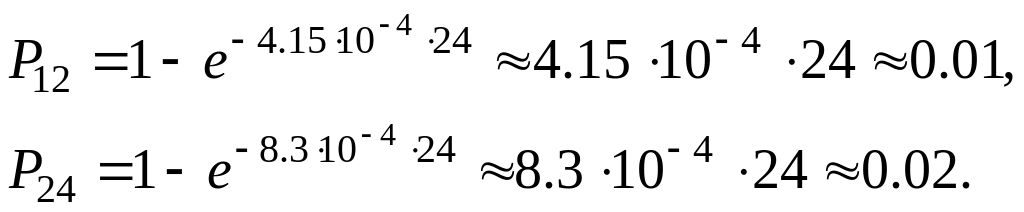
Т.к. генераторы однотипны, то:

Матрица переходных вероятностей:

Имея матрицу переходных вероятностей и зная начальное распределение вероятностей, можно рассчитать вероятность пребывания системы в одном из возможных состояний на 1-м шаге процесса.

Для : оба генератора исправны.

Это означает , .

Используем рекурентное соотношение:

.

Можно рассчитать

: .

:

:

:

:

Теперь можем аналогично получить распределение вероятностей на 2-м шаге процесса:

Из рассмотрения следует, что при каждом шаге процесса вероятность пребывания системы в работоспособном состоянии будет уменьшаться, а вероятность отказа – возрастать.

Стационарный режим для цепи Маркова.

Уравнения для финальных вероятностей цепи Маркова.

При выполнении определенных условий с увеличением номера шага k в цепи Маркова может установиться стационарный режим, при котором вероятность пребывания системы в одном из возможных состояний уже не является функцией шага:

– предельные вероятности (финальные).

Чтобы существовал стационарный режим, необходимо выполнение следующих условий:

1) Множество всех состояний системы должно быть эргодическим. Т.е. система не должна содержать источников и поглощающих состояний.

2) Цепь Маркова должна быть однородной: .

3) Случайный процесс, протекающий в системе, не должен быть циклическим. Т.е. моменты попадания в одно из возможных состояний не должны быть кратны величине шага.

Будем считать, что условия выполнены.

Тогда рекурентное соотношение будет иметь следующий вид:

.

Из суммы, стоящей справа, выделим вероятность задержки:

Отсюда, задавая значения , будем иметь систему для финальных вероятностей, состоящую из однородных алгебраических уравнений.

Для того чтобы система имела единственное решение, необходимо любое из уравнений заменить нормировочным: .

Получим систему:

– имеет единственное решение.

Система удобна при знании переходной матрицы.

Для удобства расчета финальных вероятностей по графу преобразуют систему.

Произведение будем называть потоком вероятности, переводящим систему из состояния в состояние .

.

Система примет следующий вид:

Уравнения для финальных вероятностей могут быть составлены по следующему мнемоническому правилу:

Сумма потоков вероятностей, переводящих систему из состояния в состояние равна суммарному потоку вероятности, выводящему систему из состояния .

Для рассматриваемого примера, очевидно, отсутствуют финальные вероятности, т.к. в нем не выполняется условие существования стационарного режима (условие №1).

При рассмотрении данного примера мы считаем, что отказавший генератор не ремонтируется. Такие системы называются системами без восстановления.

Если же производится ремонт отказавшего изделия, то – система с восстановлением.

Пусть в примере производится немедленное восстановление отказавшего генератора, причем количество ремонтных бригад не ограничено (т.е. возможно одновременно восстановление двух генераторов).

Пусть интенсивность восстановления ,

Т.к. возможно одновременное независимое восстановление генераторов, то

Решая систему уравнений, будем иметь:

Марковский процесс с дискретными состояниями

и непрерывным временем.

На практике моменты возможных переходов системы из состояния в состояние довольно редко известны и фиксированы (цепи Маркова).

Гораздо чаще переход системы из состояния в состояние (отказ какого-то элемента) происходит в случайные моменты времени.

Случайный процесс с дискретными состояниями и непрерывным временем называется Марковским, если для любого момента времени условные вероятности всех состояний системы зависят только от того, в каком из возможных состояний система находилась в момент времени , и не зависит от того, когда и каким образом система попала в состояние .

Для расчета Марковского процесса, т.е. нахождения вероятностей любого из состояний нам, по аналогии с цепями Маркова, необходимо знать начальное распределение вероятностей пребывания системы в одном из возможных состояний и матрицу переходных состояний.

В этом случае будет зависеть от непрерывного времени и характеризовать вероятность перехода системы из состояния в состояние за интервал времени , примыкающий к .

Но т.к. моменты переходов являются случайными величинами, то непосредственное задание переходных вероятностей невозможно

Закон распределения случайных моментов времени перехода системы из одного состояния в другое задается случайным потоком.

Т.е. в общем случае для любого из состояний задан случайный поток, каждое из событий которого – это переход системы в какое-либо из возможных состояний.

Т.о., переход системы из состояния в состояние состоит из двух зависимых событий: сначала – событие из случайного (управляющего) потока, а затем, собственно, переход системы из состояния в состояние.

Для рассматриваемой системы энергообеспечения, находящейся в состоянии , воздействует случайный поток (стирание щеток). И событие из этого потока (щетка сломалась) приводит к переходу системы из состояния в состояние или .

Чтобы случайных процесс, протекающий в системе был Марковским, необходимо, чтобы управляющий поток удовлетворял ряду требований, т.е. он должен быть пуассоновским.