Нечеткие игровые модели

Теория игр – это математическая теория конфликтных ситуаций, занимающаяся разработкой различного рода рекомендаций по принятию оптимальных решений в условиях конфликта.

Предметом изучения теории игр является математический анализ формализованной модели конфликта, учитывающий особенности реальной конфликтной ситуации.

Формализованная модель конфликта в теории игр называется игрой. Игра ведётся по определённым правилам, которые чётко определяют права и обязанности сторон, участвующих в игре, а также исход игры – выигрыш или проигрыш. Конфликтующие стороны называются игроками. Одна реализация игры называется партией. Выбор игроком того или иного действия называется ходом. Ходы бывают личные (игрок сознательно принимает то или иное решение) и случайные (исход игры не зависит от воли игрока). Набор правил, которые определяют, какой ход игроку необходимо сделать, называется стратегией. Стратегии бывают чистыми (неслучайные решения игроков) и смешанными (стратегию можно рассматривать как случайную величину).

Основная задача теории игр состоит в определении оптимальных стратегий игроков.

Основоположником теории игр является американский математик  Дж. Данциг. Он же в 1957 г. установил взаимосвязь теории игр с линейным программированием.

 

Существуют различные виды игр, укажем основные.

1.      В зависимости от количества игроков выделяют парные и множественные игры.

2.      В зависимости от количества стратегий выделяют конечные и бесконечные игры.

3.      В зависимости от вида ходов выделяют стратегические игры (все ходы личные) и азартные (все ходы случайные).

Теория игр занимается изучением только стратегических игр. В настоящее время наиболее простой и проработанной является теория матричных игр двух игроков с нулевой суммой. «Нулевая сумма» означает, что сумма выигрыша одного игрока равна сумме  проигрыша другого.

Для примера рассмотрим конечную игру двух игроков А и В, в которой игрок А может применить одну из стратегий

а игрок В – одну из  стратегий

Будем предполагать везде далее, что игрок А выигрывает, а игрок B проигрывает

Пусть каждая из сторон выбрала стратегии  и  соответственно ( фиксированы, ). Через  обозначим исход игры (сумму выигрыша игрока А или, что то же, сумму проигрыша игрока В). Предположим, что нам известны значения  при всех   Эти значения можно записать в виде матрицы, строки которой соответствуют стратегиям игрока А, а столбцы – стратегиям игрока В:

Эту матрицу будем называть платёжной матрицей. Величина

называется нижней чистой ценой игры или максимином, а величина

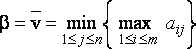
называется верхней чистой ценой игры или минимаксом.

Чистую стратегию игрока А, гарантирующую ему максимальный выигрыш, называют максиминной, а чистую стратегию игрока В, гарантирующую ему минимальный проигрыш, – минимаксной стратегией. Максиминная и минимаксная стратегии называются оптимальными стратегиями игроков А и В соответственно.  Принцип, который определяет выбор игроками своих оптимальных стратегий, называют принципом минимакса.

В теории матричных игр доказывается, что  Решение матричной игры, т. е. нахождение наилучших способов её ведения, производится по–разному, в зависимости от того,  или  Рассмотрим эти случаи.

1. Если , то величина  называется ценой игры. Подобные игры называются играми с седловой точкой, а элемент платёжной матрицы , соответствующий максиминной () и минимаксной () стратегиям игроков, называется седловым элементом(седловой элемент – это элемент платёжной матрицы, наименьший в своей строке и наибольший в своём столбце).

Следует отметить, что оптимальные стратегии игроков в играх с седловой точкой обладают тем свойством, что отклонение от своей оптимальной стратегии только одного игрока может лишь ухудшить положение отклонившегося.

2. Решение матричной игры с  находят, используя так называемые смешанные стратегии игроков – случайное чередование отдельных чистых стратегий с определённой вероятностью.

Смешанную стратегию игрока А, состоящую из чистых стратегий  с соответствующими вероятностями  будем обозначать как вектор

 

Смешанную стратегию игрока В, состоящую из чистых стратегий  с соответствующими вероятностями  будем обозначать как вектор

 

При этом, по свойствам вероятности случайного события, необходимо учитывать, что

и

Применение игроком А отдельной чистой стратегии  () можно рассматривать как частный случай смешанной стратегии, в которой вероятность применения им стратегии  равна единице, а вероятности применения других стратегий равны нулю. Следовательно, величина выигрыша игрока А (проигрыша игрока В) является случайной величиной с возможными значениями  элементов платёжной матрицы.

Средняя величина выигрыша (проигрыша) является функцией от смешанных стратегий и имеет вид

Эта функция называется платёжной функцией игры с платёжной матрицей 

Пусть   − оптимальные смешанные стратегии игроков А и В соответственно. Справедливы неравенства:

 

 

которые означают, что применение игроком А оптимальной смешанной стратегии  гарантирует ему выигрыш, не меньший, чем при применении им любой другой стратегии  в свою очередь, применение игроком В оптимальной смешанной стратегии  гарантирует ему проигрыш, не больший, чем при применении им любой другой стратегии  Величина  в этом случае определяет цену игры.

Совокупность оптимальных смешанных стратегий ,  и цены игры  составляет решение матричной игры.

Точное задание элементов платежной матрицы матричной игры, как правило, затруднено из-за недостаточности, неточности исходной информации или неточности модели исследуемой системы, что особенно характерно для экономических систем. В этом случае, предлагается задавать элементы платежной матрицы в виде нечётких чисел a_ij , i=1…n, j=1…m, где n – число чистых стратегий игрока 1; m- число чистых стратегий игрока 2. Нечёткие числа полностью описываются своими функциями принадлежности _ij (x), которые определяются или экспертным опросом или на основе нечёткой модели исследуемой системы. Таким образом, возникает нечёткая матричная игра. В данной статье предлагается методика решения таких игр и анализа чувствительности и стабильности полученного решения.

Решение любой матричной игры (n  m) может быть сведено к решению пары двойственных задач линейного программирования. Однако в случае нечёткой матричной игры возникает проблема в использовании для решения этих задач симплекс-метода, связанная с делением на нечёткие числа, носитель которых содержит нуль. Эта операция над нечёткими числами неопределена 1. Для избежания этой проблемы предлагается решать нечёткие матричные игры итерационным методом Брауна-Робинсона, для которого не требуется деления на нечёткие числа , а осуществляются лишь операции сложения и сравнения нечётких чисел.

Все арифметические операции осуществляются просто, если нечёткие числа задавать трапецеидальными функциями принадлежности (боковые ветви (х) описываются линейной функцией). Как показано в работах Василевича, задание боковых ветвей (х) другим образом практически не изменяет решения, но усложняет выполнение арифметических операций. При использовании трапецеидальных функций любое нормальное нечёткое число задаётся четырьмя параметрами (а₁,в₁,в₂,а₂) , где а₁ и а₂ – определяют нижнюю и верхнюю границы носителя n нечёткого числа, а в₁ и в₂ - соответственно границы ядра r.

В этом случае нормальное нечёткое число А , равное сумме двух нормальных чисел с параметрами (а₁,в₁,в₂,а₂) и (с₁,б₁,б₂,с₂) будет определяться в соответствии с принципом обобщения Заде параметрами (а1+с1,в1+б1,в2+б2,а2+с2).

При сравнении нечётких чисел можно использовать различные индексы ранжирования. В частности, предлагается использовать индекс ранжирования, вычисляемый по формуле:

H_A =  A_{ +} + (1-) А_{ ,} (1)

где A_{ +} - max A_ ; A_ - min A_ ; A_ - срез нечёткого числа А на уровне  ;   0 , 1 и отражает степень рискованности лица принимающего решение (обычно берут = 0,5). Аналогично вычисляется H_В. Далее процедура сравнения сводится к определению отношения H_A\ H_В. Если H_A  H_В, то в соответствии с данным индексом ранжирования считается, что А В, а величина отношения определяет степень их отличия. Можно использовать и другие индексы ранжирования.

В результате решения конечной матричной игры методом Брауна- Робинсон будут получены чёткие квазиоптимальные , в общем случае, смешанные стратегии игроков S_A = \p₁,p₂,…,p_n\ и S_B = \g₁,g₂,…,g_n\ и нечёткая цена игры

V = 1\2 ( min _j + max _i ), (2)

где _j- суммарный выигрыш игрока А за k итераций для j-ой стратегии игрока 2; _i - суммарный выигрыш игрока В за k итераций для i-ой стратегии игрока 1.

После получения решения нечёткой игры возникает задача оценки чувствительности и стабильности полученного решения от задания нечётких элементов платёжной матрицы.

Предлагается методика решения этой задачи на основе оценок показателей размытости цены игры V и элементов платёжной матрицы a_ij . В качестве показателя размытости d_A нечёткой величины А, хХ, _А (x)  0,1, будем рассматривать функционал аналогичный шенноновской энтропии:

_

d_A= -  _А (x) ln _А (x) dx. (3)

_-

Выбор показателя размытости не оказывает влияния на общий подход к оценке чувствительности и стабильности нечёткой матричной игры, определения которых приводятся ниже.

Определение1. Дифференциальной чувствительностью К_ij нечёткой матричной игры к нечёткому заданию элемента a_ij её платёжной матрицы является отношение относительного приращения  d_v \ d_v показателя размытости d_v цены игры V к относительному приращению  d_ij \ d_ij показателя размытости d_ij нечёткого элемента a_ij , вызвавшего изменения в цене игры:

К_ij = ( d_v \ d_v) \ (  d_ij \ d_ij) =  ln d_v \  ln d_ij . (4)

При оценке чувствительности системы к одновременному изменению нескольких элементов платёжной матрицы игры суммарная чувствительность

К_ =  К_ij. (5)

^{i j}

Определение 2. Нечёткая игра обладает свойством (- стабильности к изменению элементов платёжной матрицы, если при изменении суммы модулей относительных изменений показателей размытости этих элементов в пределах  (   d_ij \ d_ij   ) модуль относительного изменения показателя размытости цены игры не превышает  (  d_v \ d_v   ).

Анализ чувствительности и стабильности нечётких игр легче проводить, если использовать ряд свойств показателя размытости нечёткого числа, которые были определены в книге Василевича. Применим предлагаемую методику для следующего случая. Пусть во всех элементах платёжной матрицы нечёткой матричной игры расширили носитель на n. В этом случае, показатель размытости каждого элемента в соответствии со свойствами, приведенными автором, изменится на

 d_ij = 0.25n. (5)

Показатель размытости цены игры, определяемой в соответствии с методом Брауна – Робинсон по формуле (2), также изменится на величину

 d_v = 0.25n. (5)

Это следует из свойства матричных игр, заключающегося в том, что прибавление одного и того же числа ко всем элементам платежной матрицы не изменит оптимальные стратегии, а лишь на эту величину изменит цену игры 2. В рассматриваемом случае ко всем элементам был прибавлен нечёткий нуль с носителем n. Тогда получаем, что чувствительность

К_ij = ( d_v \ d_v) \ (  d_ij \ d_ij) = d_ij \ d_v. (6)

К_ =  К_ij =  d_ij \ d_v n m, (9)

^{i j i j}

где d_v =  p_i g_j d_ij .

^{i j}

Далее получаем, что нечёткая матричная игра обладает свойством (- стабильности, если одновременно выполняются два неравенства:

n  4 d_ij \ n m; (7)

n  4 d_v. (8)

Как видно из неравенства (7), при увеличении размерности игры стабильность уменьшается, т.е. увеличение числа чистых стратегий игроков вынуждает оценивать элементы платёжной матрицы более тщательно. В частном случае, для n = m =5;  = 0,5 и  = 0,1 получаем, что изменения носителей элементов платёжной матрицы могут быть до половины d_ij = 0,25( n_ij - r_ij ) и до половины

d_v = 0,25( n_v - r_v ), что свидетельствует о большой устойчивости данной игры. Оценки чувствительности и стабильности нечётких матричных игр позволят определить требования к проведению экспертного опроса при получении соответствующих функций принадлежности элементов платёжной матрицы игры.

Эффективность функционирование указанных интеграционных образований, направленное на повышение конкурентоспособности входящих в них предприятий, в значительной степени определяется согласованностью действий участников по реализации стратегии инновационного развития и их заинтересованностью в консолидированном результате. Анализ подходов к построению экономико-математических моделей для поддержки принятия решений по выбору стратегии инновационного развития интеграционных образований хозяйствующих субъектов показывает целесообразность применения алгоритмов коалиционных игр .

Укажем, что, несмотря на всю развитость теории игр, для поддержки принятия решений по выбору стратегии инновационного развития интеграционных образований в промышленности данный аппарат применяется крайне мало или совсем не используется. Возможными причинами этого являются крайняя трудность численного определения элементов платежной матрицы (характеристической функции для кооперативных игр), т.е. выигрыша или потерь сторон при применении той или иной стратегии, и вероятностный характер оптимальных смешанных стратегий. Действительно, в большинстве случаев задачи выбора инновационной стратегии имеют уникальный, единичный характер.

Обзор литературных источников между тем показывает, что приведенные сложности могут быть устранены при использовании в игровых моделях аппарата нечеткого логического вывода , с помощью которого как выигрыши и потери, так и возможные стратегии игроков выражаются в терминах нечетких множеств. 

Для простоты, рассмотрим вначале модель нечеткой игры только двух игроков (противников). Пусть как игрок A, так и игрок B придерживаются только чистых стратегий, соответственно, A1Am и B1Bn. Игрок A ничего не знает о стратегии, которую выберет игрок B, но может провести однократный эксперимент (разведку), результатом которого является измеренный вектор X = (x1, x2, …, xd) факторов, отражающих состояние (намерения) игрока B (возможен вариант игры без изучающего эксперимента, года степени уверенности о выборе противником той или иной стратегии оцениваются экспертным путем). Предполагается, что игра носит уникальный (единичный) характер и отображается матрицей выигрышей игрока A. Если предположить, что выигрыши aij  являются нечеткими переменными (числами), например, с именами "малые выигрыши", "средние выигрыши", "большие выигрыши" и т.д., и характеризуются функциями принадлежности , где y – выражение выигрышей в количественной форме, Ai – выбранная стратегия первого игрока, а степень уверенности, что при измеренном значении X игроком B выбрана стратегия Bj, отражается значением  (1) где  - некоторые функции принадлежности, устанавливаемые экспертным путем (смысл которых – степень принадлежности фактора xk планируемой стратегии ). Выигрыши игрока A при выборе им стратегии Ai могут быть описаны совокупностью (блоком) нечетких продукционных правил: 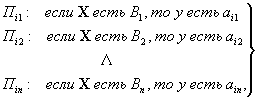 (2) где предпосылка "если X есть Bj" представляет собой сокращение записи "", где, в свою очередь, bjk – термы, соответствующие функциям принадлежности . В условиях приведенной игровой модели требуется: определить такую чистую стратегию Ag* игрока A, при которой обеспечивается его наибольший выигрыш.

Варианты нечетких игровых моделей разработаны и для коалиционных игр.

Однако в известных публикациях авторы, как правило, ограничивались введением понятия "нечеткая коалиция", не рассматривая другие компоненты игровой модели с точки зрения аппарата нечеткой логики.

Т. е. коалиционная игра определяется как пара (I, v), составленная из множества игроков I, которое предполагается не пустым и ограниченным, и характеристической функции v из множества всех коалиций в множество вещественных чисел .

Коалиция - подмножество игроков , включая К=I и пустое множество К =Ø.

Каждая четкая коалиция К может быть идентифицирована характеристический вектором коалиции (τ_K(1), τ_K(2),…, τ_K (n)) где, для каждого игрока i принадлежит I, τ_K(i)=1если i принадлежит K и τ_K(i)=0, если i принадлежитI \ K

Основные понятия нечетких игр

Нечеткая коалиция L – это нечеткое множество, определенное на множестве игроков I с функцией принадлежности

τ_L: I→[0,1] , где

значение τ_L(i) принадлежит [0,1] и представляет степень участия игрока i в нечеткой коалиции L .

Нечеткие коалиции могут рассматриваться как варианты совместного поведения игроков с различной степенью их активности.

Если L₁ , L₂, …,L_m нечеткие коалиции, представленные векторами (τ_L1(1),…, τ_L1(n)), (τ_L2(1),…, τ_L2(n)), (τ_Lm(1),…, τ_Lm(n)) и (τ_L1(i)+τ_L2(i)+…+ τ_Lm(i), то говорят о структуре коалиций.

О связи нечетких и четких коалиций

Теорема: непустой выпуклый многогранник является выпуклой оболочкой своих вершин.

Вывод: Если представить нечеткие коалиции точками единичного гиперкуба, а четкие коалиции вершинами этого гиперкуба, то каждая нечеткая коалиция может быть представлена выпуклой комбинацией четких коалиций.

Однако, такое представление не однозначно.

Оптимальное представление нечеткой коалиции

Находим выигрыш нечеткой коалиции L в виде оптимальной выпуклой комбинации значений характеристической функции:

Вместо аналитического задания характеристической функции нечеткой коалиционной игры получаем метод вычисления значения этой функции, сводящийся к решению задачи линейного программирования.

Устанавливается очевидная связь между полноценным участием или неучастием в коалиции и частичным присутствием в ней.

Оптимальное представление нечеткой коалиционной структуры

Эффективность коалиционной структуры определяет их общий выигрыш, который зависит от распределения игроками средств в количестве единицы между нечеткими коалициями.

Для оптимизации эффективности коалиционной структуры решаем задачу линейного программирования, в которой искомыми переменными являются величины перераспределения средств каждым игроком между коалициями структуры, и коэффициенты разложения каждой из этих нечетких коалиций в выпуклую комбинацию четких коалиций.

Итоговым результатом данной теории является методика, позволяющая учесть частичное присутствие игрока в коалиции.

Возможность формирования структуры, состоящей из нечетких коалиций, позволяет моделировать объединение игроков для участия в нескольких проектах одновременно любой долей своих средств.

Данная методика позволяет найти оптимальное распределение средств игрока между проектами, гарантирующее получение совместного наибольшего выигрыша.

Проведенный обзор работ и изучение практических задач позволяет конкретизировать задачу построения коалиционной игровой модели для выбора инновационной стратегии интеграционного образования развития исследования следующим образом:

1) в общем случае в игре принимают участие N игроков, при этом коалицию образуют N-1 участник против одного игрока ("противника"),

2) игра носит уникальный характер,

3) игра содержит элементы неопределенности (т.е. неполную информированность о возможных действиях противника, о величине выигрыша или потерь при выборе той или иной стратегии и т.п.), которые трудно или невозможно отразить категориями теории вероятностей, но можно выразить в лингвистической форме; Примем следующую математическую формулировку нечеткой игровой модели. Дано: 1) множество вариантов {Bj}, , предполагаемых действий игрока N ("противника"); 2) множество вариантов или стратегий {Asi}, , , s-го участника коалиции; *Замечание: {Bj} и {Asi} – это инновационные стратегии, означающие выполнение определенной последовательности действий; 3) набор признаков {xk},  среди которых могут быть как количественные (непрерывные), так и качественные (дискретные); 4) набор функций принадлежности jk(xk), отражающих степени уверенности, что при фактически наблюдаемом признаке x*k игроком N будет избран вариант поведения Bj, или набор значений j степеней уверенности о выборе игроком N той или иной стратегии; 5) набор термов (т. е. имен) asij, , лингвистической переменной "выигрыш" (выигрыш игрока s), например, as11 – "малый выигрыш", as12 – "большой выигрыш" и т.п., задаваемый с учетом стратегий выбранных предыдущими (s –1)-м участниками коалиции; 6) набор степеней принадлежности мsij, соответствующих термам asij. Требуется: найти стратегии Asg* участников коалиции, обеспечивающие их наибольший выигрыш в результате реализации инновационной стратегии развития с учетом возможных действий противника и других участников коалиции. Возможные алгоритмы решения.