Среднее время безотказной работы.

Два способа определения :

1. Фиксировать каждое значение . Но это требует либо специальной аппаратуры, либо сменной работы.

2. Не фиксируют каждого изделия, а определяют количество вышедших из строя за отрезки времени .

Условно считают, что все изделия вышли из строя точно на середине этого отрезка. И считают это время: .

Тогда:

k – количество отрезков.

дает только общее представление о надежности изделия, но никак не описывает поведение изделий во времени.

Т.е. равно площади области ниже кривой .

Пример.

Определить, на каком участке эксплуатации находится изделие.

, , .

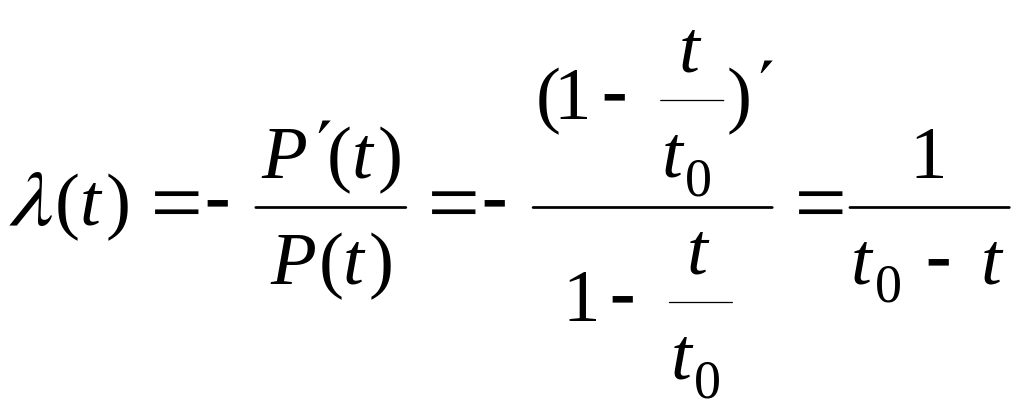Изделие находится на участке старения.

Как известно, вероятность безотказной работы изделия: .

.

Для нормального участка эксплуатации: .

.

Т.о., на нормальном участке эксплуатации:

Типовые законы распределения времени

безотказной работы изделия.

Для нахождения закона распределения , который полностью описывает поведение изделия на любом участке, можно поступить двояким образом:

– по результатам эксперимента строится ряд распределения, затем подбирается выравнивающая кривая и ищется для нее теоретическое описание;

– используют типовые законы распределения, описывающие поведение изделия на некоторых участках или на протяжении всей жизни изделия, и подбирают коэффициенты этих типовых законов.

1) Экспоненциальный закон распределения.

Функция распределения: .

– параметр закона распределения

Описывает работу изделия на нормальном участке эксплуатации.

Свойства экспоненциального закона:

1. .

2. Вероятность отказа изделия, проработавшего безотказно , не зависит от продолжительности этого времени, а определяется длиной интервала .

В данном случае будем иметь: количество изделий, отказавших на интервале , не зависит от количества изделий, отказавших на других интервалах, и для поддержания необходимо, чтобы с увеличением времени уменьшалось количество изделий, отказавших на интервале , т.е. говорят, что изделие "не помнит себя в прошлом".

3. Вероятность того, что изделие откажет через время равна:

Экспоненциальный закон имеет очень простые формулы для расчетов. Поэтому его используют в качестве первого приближения на любом участке эксплуатации.

2) Закон Вейбулла.

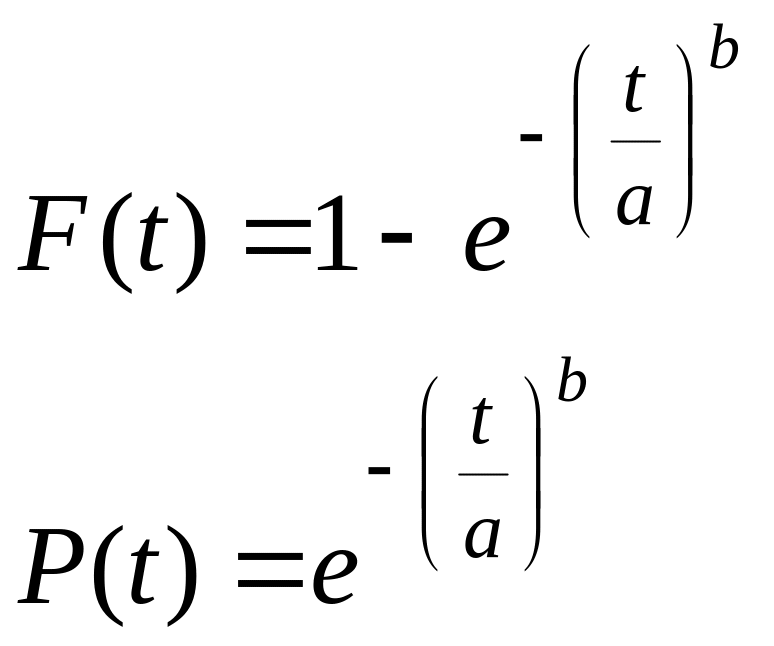
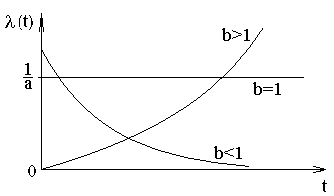
Рассмотрим поведение изделия при :

– описывает поведение изделия на нормальном участке эксплуатации.

Если :

– описывает поведение изделия на участке старения.

Если :

– описывает поведение изделия на участке приработки.

3) Усеченный нормальный закон распределения.

Т.к. случайная величина, характеризующая работу изделий (наработка на отказ, количество замыканий реле и т.д.) представляет собой только положительные значения, то для описания поведения изделия может использоваться усеченный нормальный закон распределения.

Усеченный нормальный закон распределения получают из нормального при ограничении интервала возможных изменений случайной величины.

, – нормирующий коэффициент.

.

Коэффициент находится из условия:

.

– произвольный участок изменения случайной величины .

Если , то в этом случае мы произведем нормирование и центрирование случайной величины.

Тогда: , где .

– нормированная функция Лапласа – интеграл вероятности:

Вероятность безотказной работы изделия будет определяться следующим образом:

.

Для полубесконечного интервала найдем:

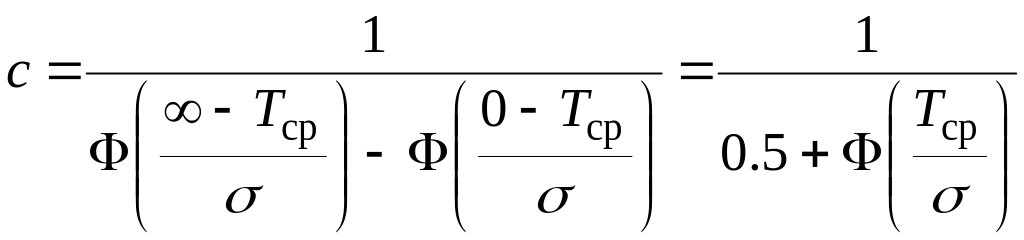
Если , то тогда . И тогда .

При использовании нормального закона в первую очередь проверяется, острое это распределение или нет, т.е. условие . Если да, то . Далее для заданной наработки находится , а затем рассчитывается вероятность безотказной работы изделия.

Нормальный закон распределения описывает работу изделия на участке старения.

Пример.

Известно, что средняя наработка на отказ изделия .

Найти время, в течение которого будут работоспособны 90% изделий. При этом рассматривать работу изделия на разных участках эксплуатации.

1. Участок приработки.

Пусть .

Для закона Вейбулла:

.

,

2. Участок нормальной эксплуатации.

,

3. Участок старения.

, , .

По таблице найдем: .

,

Индивидуальная проработка.

Надежность типовых радиоэлектронных элементов.

Факторы, влияющие на надежность изделия, и пути повышения надежности.

Расчет надежности систем с независимыми

отказами элементов.

Для расчета надежности системы необходимо построить модель надежности, которая строится на основании функциональных схем.

В случае независимых отказов модель надежности представляется в виде логической схемы взаимодействия между элементами, которая называется структурной функцией надежности.

Пусть система может находиться в 2-х состояниях:

– работоспособном (Y=1);

– неработоспособном (Y=0).

Вероятность пребывания системы в работоспособном состоянии:

.

Вероятность отказа системы:

.

Состояние системы зависит от состояния элемента.

Будем также считать, что каждый элемент может находиться в двух состояниях:

– работоспособном ( );

– неработоспособном ( ).

Вероятности нахождения элементов в состояниях:

Функция Y, связывающая состояние системы с состояниями входящих в нее элементов, называется структурной функцией надежности.

– СФН.

Для двоичных переменных структурная функция надежности является функцией алгебры логики и может быть задана в трех видах:

1) словесное описание

2) в виде таблицы состояний

3) функцией алгебры логики

Пример. Система ориентации спутника содержит 3 датчика. Система работоспособна, если работоспособны хотя бы 2 датчика.

(строки и столбцы переставлены для удобства)

	1	0	1	1	0	0	1	0
	1	1	0	1	0	1	0	0
	1	1	1	0	1	0	0	0
	1	1	1	1	0	0	0	0