
Расчетно-графическая работа №23
.DOC
Уфимский Государственный Авиационный Технический Университет
Кафедра теоретических основ электротехники
РАСЧЕТНО–ГРАФИЧЕСКАЯ РАБОТА № 2
“ПЕРЕХОДНЫЕ ПРОЦЕССЫ”
Выполнил: студент гр.Т28-219
Матвеев А.В.
Принял: Енгалычев И.Р.
Уфа – 2003
Дано:



 Е = 220 В,
Е = 220 В,
R2

 R1
= 10 Ом,
R1
= 10 Ом,
L
R3

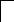 R3
= 94 Ом,
R3
= 94 Ом,
R4 = 55 Ом,
R1

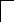
 L
= 61 мГн
L
= 61 мГн

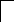
R4
C = 11 мкФ
C
i3


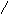

i2
i1
Uc




E
схема 2


-
Запишем ток i1 в общем виде:
i1(t) = iуст + iсв
-
Найдем установившийся ток.
Учитывая, что конденсатор не пропускает постоянный ток, а катушка проводит его, как простой проводник получим, что через бесконечно большой промежуток времени схема примет вид:




R2


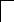
R3
R1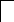
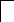



R4
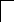

i3

E
i2
Uc



i1






Установившийся ток равен:
I1уст
=
![]()
![]() =
2,1154 А
=
2,1154 А
I2уст = 0 А
![]()
-
Найдем характеристическое сопротивление цепи и приравняем его к нулю:
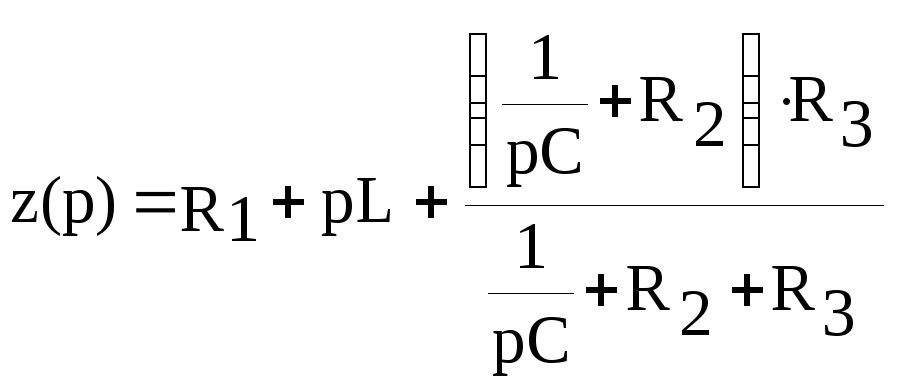
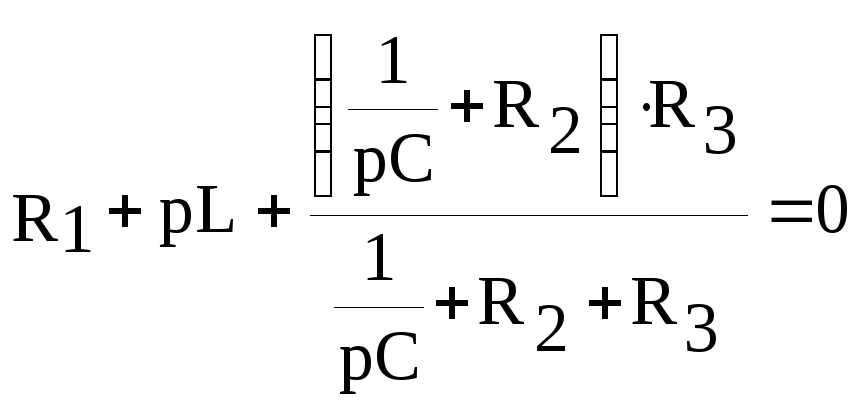
p2
(L*
R2+L*
R3)
+ p ( R1*R2
+
R2
R3+
R1
*R3
+![]() )
+
)
+
![]() = 0
= 0
![]()
Получили характеристическое уравнение:
0,000116083*р2 + 0,161716*p + 104 = 0
Решая его получим:
р1 = – 696,55+640,88j
р2 = – 696,55 – 640,88j
Корни комплексно-сопряженные, значит:
I1св![]()
-
Найдем постоянные коэффициенты А и ψ.
Для этого используем первый и второй закон коммутации:
Ток в цепи, содержащей индуктивность, не может измениться скачком.
И Uc(0-)= Uc(0+)
I2(0-)=1,39 A
i1(
0-)
=
i1(0+)
=
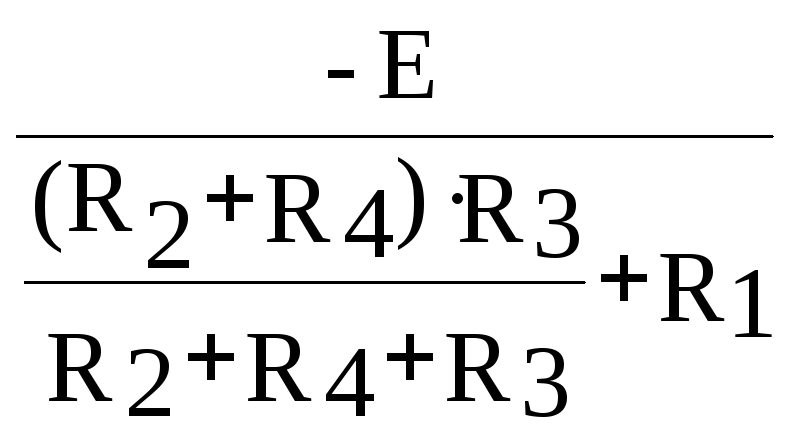 =
- 3,38 A
=
- 3,38 A
Uc(0-)= R4*I2=76,45 В
Найдем ток I2(0+) . Для этого составим систему уравнений по законам Кирхгофа:
I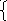 1(0+)
+
I2(0+)
+I3(0+)
= 0
1(0+)
+
I2(0+)
+I3(0+)
= 0
Uc(0+)+I2(0+)*R2 – I3(0+)*R3 = 0
I3(0+)
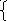 =
3,38 – I2
(0+)
=
3,38 – I2
(0+)
I2(0+)*79 + 76,45 – 94(3,38 – I2 (0+)) = 0
I2(0+)=1,395 A I3(0+)=1,985 A
Запишем уравнение
цепи:
![]()
Подставляя числовые
значения найдем
![]() :
:
![]() ≈
6,97
≈
6,97
Составим систему:
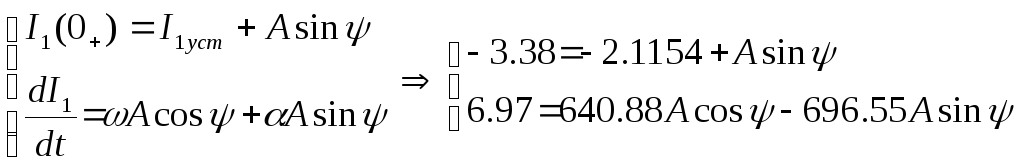
Решая данную систему получим:
А = - 1,854
Ψ = 43ْ
Таким образом:
I1(t)= - 2,1154 – 1,854e -696,55tsin(640,88t + 43)
Построим график
искомой величины на интервале от t=0
до
![]()
![]()
![]()
