Министерство образования Российской Федерации

Кафедра теоретических основ электротехники

РАСЧЕТНО–ГРАФИЧЕСКАЯ РАБОТА № 2

“ПЕРЕХОДНЫЕ ПРОЦЕССЫ”

Выполнил:

студент группы АСОИ-216

Немцев М.М.

Принял:

преподаватель Грахов П. А.

Уфа 2000 г.

Дано:

Е = 140 В,

R₁

R₂

R₃

R₁ = 40 Ом,

R₂ = 50 Ом,

R₃ = 10 Ом,

C

L

U_c

L = 80 мГн

C = 200 мкФ

i₂

Найти:

i₁

i₃

i₁(+ 0),

E

схема 1

.

– 1 –

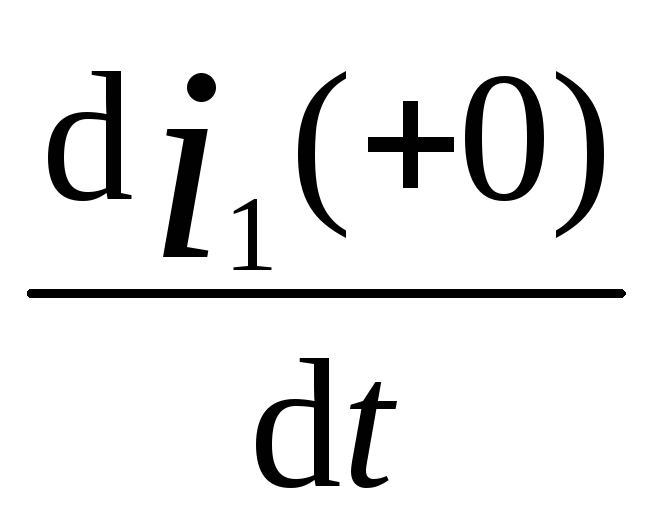1. Запишем ток i₁ в общем виде:

i₁(t) = i_уст + i_св

2. Найдем установившийся ток.

Учитывая, что конденсатор не пропускает постоянный ток, а катушка проводит его как простой проводник получим, что через бесконечно большой промежуток времени схема примет вид:

R₁

R₂

R₃

E

Очевидно, что установившийся ток равен нулю.

i_уст = 0

3. Найдем свободный ток.

Для этого найдем характеристическое сопротивление цепи и приравняем его нулю.

p² L C + p C ( R₁ + R₂ ) + 1 = 0

Получили характеристическое уравнение:

1,6*10^-5 р² + 1,8*10^-2 + 1 = 0

Решая его получим:

р₁ = – 62,5

р₂ = – 1062,5

Корни вещественные, значит уравнение свободного тока имеет вид:

– 2 –

4. Найдем постоянные коэффициенты А₁ и А₂ .

Для этого используем первый закон коммутации:

Ток в цепи, содержащей индуктивность, не может измениться скачком.

i_L(– 0) = i_L(+ 0) = i₁(– 0) = i₁(+ 0) = =1,55 A.

Запишем второй закон Кирхгофа для данной цепи:

R₁ i₁ + L–i₂ R₂ – U_C = E,

отсюда, при t = 0 имеем:

R₁ i₁⁰ + L+i₁⁰ R₂ = E,

==0.

Составим систему:

Подставляя найденные значения р₁ и р₂ и решая данную систему получим:

А₁ = 1,65,

А₂ = –0,097

Таким образом:

i₁(t) = 1,65 е^{–62,5 t} – 0,097e^{–1062,5 t}

= –103,1 е^{–62,5 t} + 103,1 e^{–1062,5 t}

|₀ = 0.

– 3 –