2.2 Построение стереографической проекции всех элементов симметрии заданной точечной группы

Задание 2 выполняется на кальке с помощью сетки Вульфа. Наложите кальку на сетку Вульфа и сделайте отметки центра круга проекций и . Затем надо нанести стереографическую проекцию кристаллографической системы координат, выполнив следующие правила:

• проекция оси всегда совпадает с центром круга проекций;

• проекция оси всегда совпадает с отметкой , если только заданная точечная группа не относится к моноклинной сингонии.

Используя стандартные установки и правила записи символа, сначала нанесите на кальку формульные элементы. Затем, вращая ось

Рис. 5 Рис. 6

третьего порядка вокруг вертикальной инверсионной оси по правилам поворота проекций с помощью сетки Вульфа получим еще три наклонных оси третьего порядка. На последующих рисунках, чтобы их не загромождать, не задействованные элементы опущены.

Для поворота плоскости, в общем случае, нужно перейти к ее гномостереографической проекции, затем повернуть плоскость проекций так, чтобы ось, вокруг которой совершается поворот, совпала с центром круга проекций. Выполнив повороты гномостереографической проекции плоскости, вернутся к исходной ориентации плоскости проекции и по гномостереографическим проекциям плоскостей построить их стереографические проекции.

Для плоскости, проходящей через ось и перпендикулярной кругу проекций, эта задача упрощается. Нужно повернуть кальку так, чтобы стереографическая проекция плоскости легла на горизонтальный диаметр круга проекций, тогда в нашем случае по вертикальному меридиану проходит вторая вертикальная плоскость.

Рис. 7 Рис. 8

Вновь появившаяся плоскость теперь проходит через наклонную ось 3 и таких плоскостей должно быть три. Для нахождения их проекций нужно выполнить ранее изложенные построения, последовательность которых показана на приведенных ниже рисунках.

Рис. 9 Рис. 10

Рис. 11

П овернув, таким образом вокруг всех наклонных осей оставшиеся плоскости и оси симметрии, получим окончательно стереографическую проекцию всех элементов симметрии точечной группы . Как правило, выполнять вращение вокруг всех осей нет необходимости, т.к. одна и та же плоскость проходит через несколько осей, а одна и та же ось симметрии пересекает несколько других.

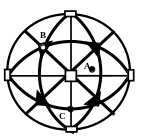Рис. 12

2.3 Определение углов между всеми осями симметрии и плоскостями зеркального отражения.

После построения стереографической проекции данной точечной группы с помощью сетки Вульфа, можно приступать к выполнению задания 3 – определению углов между всеми элементами симметрии данной точечной группы. Для этого необходимо стереографические проекции плоскостей перевести в гномостереографические. Затем, выводя попарно проекции элементов на один меридиан сетки Вульфа, определить углы между ними обычным способом. Результаты измерения углов вносятся в таблицу вида: Таблица 2.1.

Таблица 1. Углы между элементами симметрии.

Элементы симметрии		Оси							Плоскости
Оси		0	900	900	600	600	1200	1200	450	450	900	900	1460	340
		900	0	900	600	1200	600	1200	1350	450	340	1460	900	900
		900	900	0	450	450	450	450	900	900	560	560	560	560
		600	600	450	0	600	600	900	900	450	360	910	910	360
		600	1200	450	600	0	900	600	450	900	910	360	910	360
		1200	600	450	600	900	0	600	1350	900	360	910	360	910
		1200	1200	450	900	600	600	0	900	1350	910	360	360	901
Плоскости		450	1350	900	900	450	1350	900	0	900	540	1250	1250	540
		450	450	900	450	900	900	1350	900	0	540	1250	1250	540
		900	340	560	360	910	360	910	540	540	0	1120	710	710
		900	1460	560	910	360	910	360	1250	1250	1120	0	710	710
		1460	900	560	910	910	360	360	1250	1250	710	710	0	1120
		340	900	560	360	360	910	910	540	540	710	710	1120	0