Методика решения задачи.

1. Найти значения функции на концах отрезка 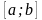, в котором лежит корень уравнения.

2. Определить знак второй производной на отрезке .

3. Если

Если

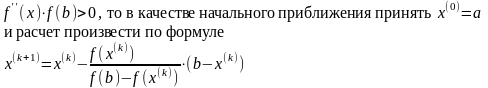
4. Если выполнено условие 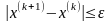то процесс завершить и положить 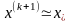, иначе положить k=k+1 и перейти к п.3.

Пример: Решить уравнение на отрезке [0,12;1] методом хорд с точностью 0,001.

Решение.

1. Найдем значение функции на концах отрезка [0,12;1]:

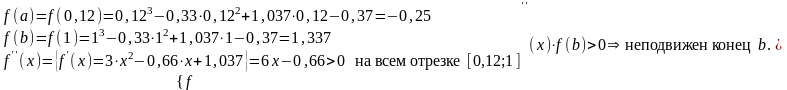
Будем пользоваться формулой:

2. Положим k=0.

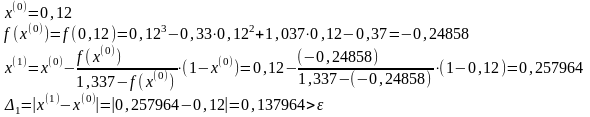
3. Положим k=1.

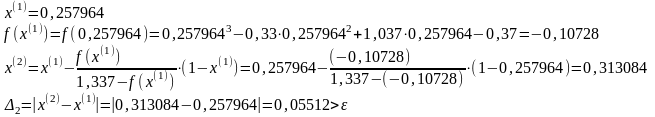
4. Положим k=2.

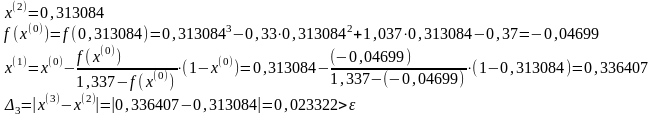
5. Положим k=3.

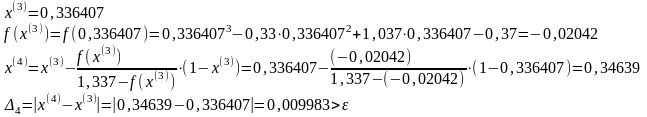
6. Положим k=4.

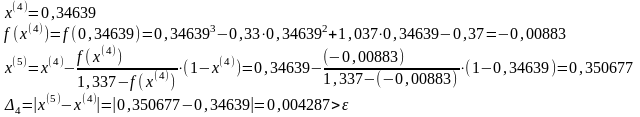
7. Положим k=5.

8. Положим k=6.

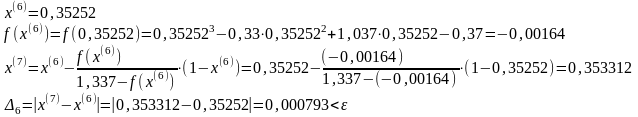
Процесс завершим и положим .

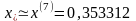Пример №2: Решить уравнение методом хорд 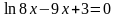на отрезке [0,0015;0,05] с точностью 0,001.

Решение.

1. Найдем значение функции на концах отрезка [0,0015;0,05]:

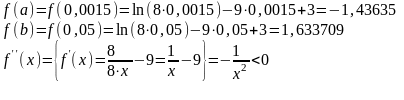
Т.о., необходимо рассмотреть уравнение

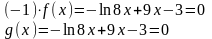
и тогда

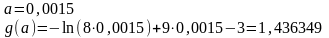
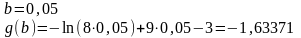
Имеем 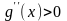на всем отрезке [0,0015;0,05], и 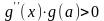- неподвижен конец а.

Будем пользоваться формулой:

2. Положим k=0.

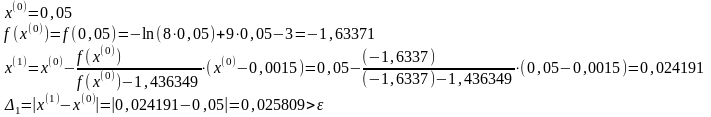
3. Положим k=1.

4. Положим k=2.

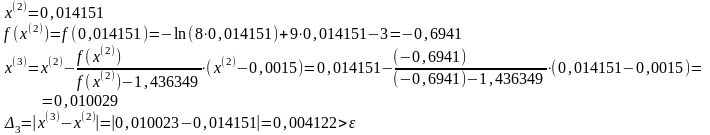
5. Положим k=3.

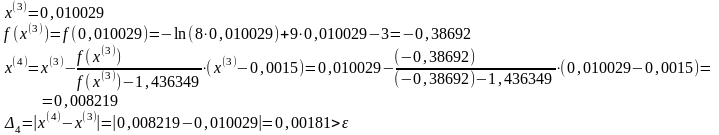
6. Положим k=4.

_{Процесс} завершен, положим _.

4. Метод касательных (метод Ньютона) решения алгебраических и трансцендентных уравнений.

Метод касательных (Ньютона) имеет квадратичную сходимость (быстро сходится) и допускает различную модификацию, приспособленную для решения векторных задач и сеточных уравнений.

Этот метод эффективен при жестких ограничениях на характер функции :

1. Существование второй производной функции на множестве .

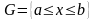2. Удовлетворение первой производной условию 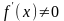для всех .

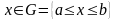3. Знакопостоянство и для всех .

Таким образом, метод Ньютона используется совместно с другими методами, чтобы достигнуть диапазона , где указанные условия начинают выполняться.

Геометрическая интерпретация метода Ньютона:

Задается начальное приближение 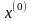. Далее проводится касательная к кривой в т. , т.е. заменяется прямой линией. В качестве следующего приближения выбирается точка пересечения этой касательной с осью абсцисс.

П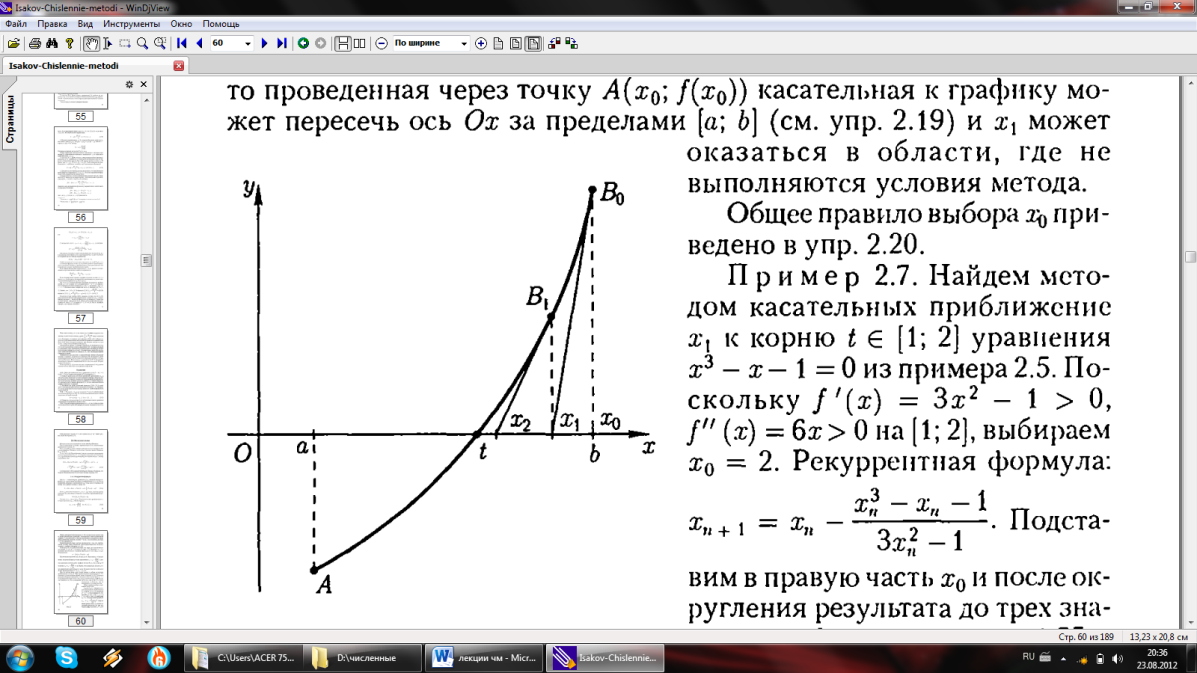 роцесс построения касательных и нахождения точек пересечения с осью абсцисс повторяется до тех пор, пока приращение не станет меньше заданной величины ɛ.

Получим расчетную формулу метода Ньютона. Вместо участка В₀t возьмём участок В₀х₁. Для этого отрезка справедливо соотношение: , где α – угол наклона касательной в точке 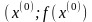к оси абсцисс. Разрешая это уравнение относительно , имеем:

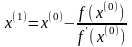
Повторяя процесс, имеем общую формулу метода Ньютона: .

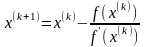Теорема №1 (о достаточных условиях сходимости метода Ньютона): Пусть выполняются следующие условия:

1. Функция определена и дважды дифференцируема на отрезке [a;b]

2. Отрезку [a;b] принадлежит только один простой корень х_* , так что .

3. и на [a;b] сохраняет знак и .

4. Начальное приближение удовлетворяет неравенству 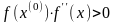(знак функции и второй производной функции совпадают).

Теорема №2 (достаточное условие сходимости метода Ньютона):

Пусть:

1. Дана функция 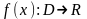, где D – открытый интервал, и непрерывна по Липшицу с на множестве D, т.е. 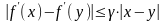, для всех х и у на D.

2. Для некоторого 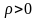выполняется условие 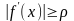для всех х из D.

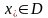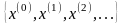Если уравнение имеет решение , то существует некоторое такое, что если , то последовательность задаваемая формулой существует и сходится к х_*. Более того, справедлива оценка .
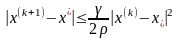