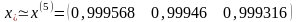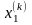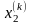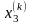- •Понятие о численных методах.
- •Погрешности вычислений.
- •3.Задача теории погрешности.
- •3.1. Абсолютная и относительная погрешность суммы и разности приближенных чисел.
- •Абсолютная и относительная погрешность произведения и частного приближенных чисел.
- •Абсолютная и относительная погрешность при вычислении функции нескольких переменных.
- •Контрольные вопросы.
- •Постановка задачи решения слу.
- •Метод простых итераций решения слу.
- •Метод Зейделя решения слу.
- •Методика решения задач.
- •Контрольные вопросы.
- •Постановка задачи решения уравнений. Отделение корней уравнения.
- •Метод половинного деления.
- •Методика решения задачи.
- •Метод хорд решения алгебраических и трансцендентных уравнений.
- •Методика решения задачи.
- •Метод касательных (метод Ньютона) решения алгебраических и трансцендентных уравнений.
- •Методика решения задач методом Ньютона.
- •Основные понятия аналитического приближения табличных функций.
- •Задача аналитического приближения табличных функций.
- •Интерполирование табличных функций.
- •Оценка погрешности полиномиальной интерполяции.
- •Интерполяционный многочлен Лагранжа.
- •5.Интерполяционный многочлен Ньютона.
- •Конечные разности.
- •Первый интерполяционный многочлен Ньютона.
- •Второй интерполяционный многочлен Ньютона.
- •Линейное интерполирование.
- •Формула линейного интерполирования.
Контрольные вопросы.
Дать определение абсолютной погрешности приближенного числа.
Как определить относительную погрешность приближенного числа?
Какая цифра в числе называется значащей?
Какие значащие цифры в приближенном числе называются верными?
Как определяется абсолютная и относительная погрешность суммы, разности, частного и произведения приближенных чисел?
Сформулируйте правило округления чисел.
Как определить абсолютную и относительную погрешность функции одной, нескольких переменных по заданной погрешности аргументов.
Выведите формулу абсолютной и относительной погрешности следующего числа:

ТЕМА №2. ЧИСЛЕННЫЕ МЕТОДЫ РЕШЕНИЯ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ.
ПЛАН.
Постановка задачи решения систем линейных уравнений (СЛУ).
Метод простых итераций решения систем линейных уравнений (СЛУ).
Метод Зейделя решения систем линейных уравнений (СЛУ).
Постановка задачи решения слу.
Прикладные задачи, характерные для проектирования современной техники, сводятся к многократным в общем случае нелинейным уравнениям, которые решаются сведением нелинейных уравнений к линейным.
Рассмотрим частный случай – линейная неоднородная задача для систем линейных уравнений, которую запишем в виде:
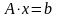 или
или
 ,
,
где
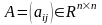 - действительная матрица,
- действительная матрица,
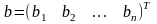 - вектор столбец,
размера (1×n),
- вектор столбец,
размера (1×n),
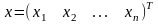 - вектор столбец
неизвестных.
- вектор столбец
неизвестных.
Необходимо
найти решение
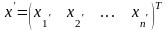 системы,
которое при подстановки в
приведет его в верное тождество.
системы,
которое при подстановки в
приведет его в верное тождество.
Характер задачи и точность полученного решения зависит от ее обусловленности.
Рассмотрим на примере:
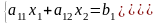 - двумерная задача
и точное решение этой задачи
- двумерная задача
и точное решение этой задачи
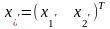 .
.
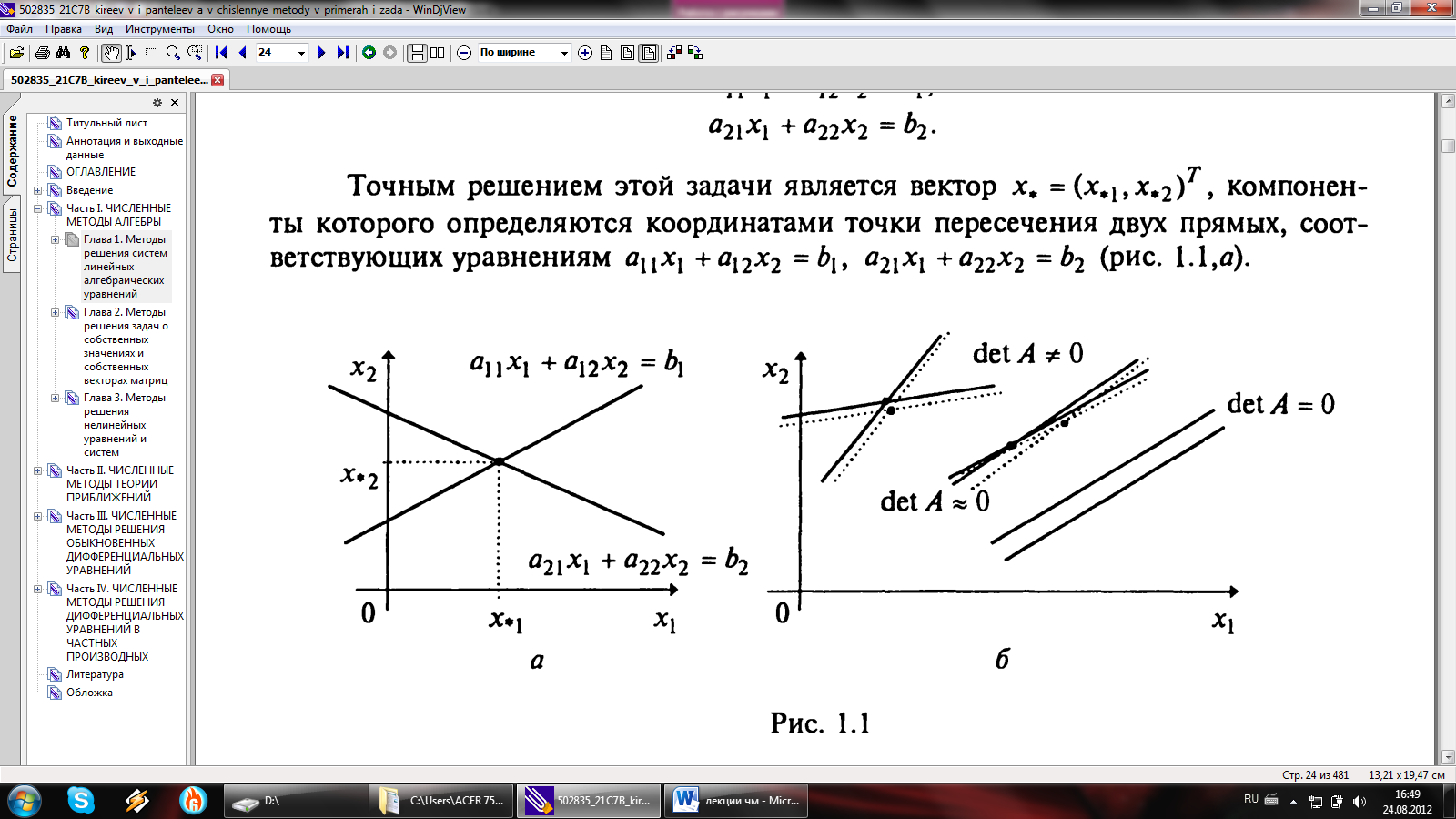
И зобразим решение этой системы:
Решение этой системы будет пересечение прямых, при этом определитель матрицы не равен нулю.
При
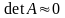 ,
небольшие погрешности в коэффициентах
могут привести к большим погрешностям
в решении, поскольку прямые близки к
параллельным – плохая обусловленность
задачи.
,
небольшие погрешности в коэффициентах
могут привести к большим погрешностям
в решении, поскольку прямые близки к
параллельным – плохая обусловленность
задачи.При
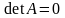 ,
прямые параллельны или совпадают, и
тогда решение задачи не существует или
оно не единственное – плохая
обусловленность задачи.
,
прямые параллельны или совпадают, и
тогда решение задачи не существует или
оно не единственное – плохая
обусловленность задачи.
Строгая обусловленность задачи характеризуется числом обусловленности:
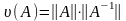 ,
,
где
 - норма матрицы А,
- норма матрицы А,
 - норма матрицы А-1.
- норма матрицы А-1.
Чем больше
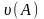 ,
тем хуже обусловленность системы.
,
тем хуже обусловленность системы.
Определение: В качестве нормы матрицы может быть принято число, которое является максимальным из суммы по модулю элементов все строк этой матрицы:
 .
.
При этом норма матрицы удовлетворяет условиям:
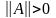 ,
при
,
при
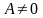 и
и
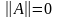 тогда и только тогда, когда матрица
А=0;
тогда и только тогда, когда матрица
А=0; ,
для всех
,
для всех
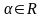 ;
; ,
где А1
и А2
некоторые матрицы;
,
где А1
и А2
некоторые матрицы;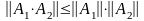 .
.
Пример: Определить норма матрицы А и норму вектора В:
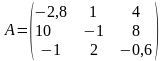

Решение.

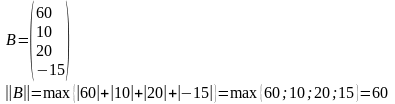
Метод простых итераций решения слу.
Метод простых
итераций основан на многократном
уточнении
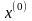 - приближенного заданного решения
системы
.
- приближенного заданного решения
системы
.
Алгоритм метода.
Исходная задача преобразуется к равносильному виду
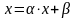 ,
где
,
где
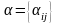 - квадратная матрица,
- квадратная матрица,
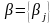 - вектор столбец. При этом для сходимости
итерационного процесса необходимо,
чтобы норма матрицы
- вектор столбец. При этом для сходимости
итерационного процесса необходимо,
чтобы норма матрицы
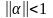 .
.
Преобразование системы к виду происходит следующим образом:
Уравнения, входящие в систему представляются так, чтобы выполнялось условие преобладания диагональных элементов
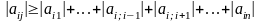 ,
,
затем первое уравнение
разрешается относительно
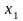 второе относительно
второе относительно
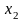 и т.д. При этом получаем матрицу
и т.д. При этом получаем матрицу
 с нулевыми диагональными элементами.
с нулевыми диагональными элементами.
Вектор
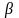 принимается в качестве начального
приближения
принимается в качестве начального
приближения
 и далее многократно выполняются действия
по уточнению решения, согласно
рекуррентному соотношению:
и далее многократно выполняются действия
по уточнению решения, согласно
рекуррентному соотношению:
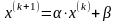
или в развернутом виде:
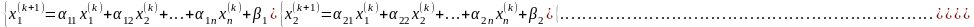
Итерации прерываются при выполнении условия:
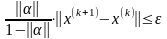 или
или
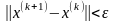
заданная точность, которую необходимо достигнуть при решении задачи.
Замечание: Начальное приближение может выбираться произвольно или из некоторых соображений.
Чтобы проверить сходимость процесса введем следующие теоремы:
Теорема №1
(достаточное условие сходимости метода
простых итераций):
Метод простых
итераций, реализующийся в процессе
последовательных приближений
сходится к единственному решению
исходной системы
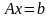 при любом
начальном приближении
со скоростью не медленнее геометрической
прогрессии, если
.
при любом
начальном приближении
со скоростью не медленнее геометрической
прогрессии, если
.
Замечание:
1. Условие теоремы №1 (как достаточное)
предъявляет завышенные требования к
матрице
,
и поэтому иногда сходимость будет, если
даже норма матрица будет больше либо
равна единице
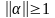 .
.
2. При допущении отдельной ошибки в вычислениях в сходящемся процессе – не отразится на окончательном результате.
3. Условие сходимости
выполняется, если в матрице
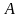 преобладают
диагональные элементы
.
преобладают
диагональные элементы
.
4. Чем меньше
величина нормы матрицы
 ,
тем быстрее сходится метод простых
итераций.
,
тем быстрее сходится метод простых
итераций.
Теорема №2 (о необходимом и достаточном условии сходимости метода простых итераций): Для сходимости последовательности , при любом и необходимо и достаточно, что бы собственные значения матрицы были меньше единицы.
Теорема №3
(о погрешности приближений вычислительных
методов):
Если в итерационном процессе норма
матрицы
,
согласованная с нормой вектора
 и
,
то справедлива следующая оценка
погрешности:
и
,
то справедлива следующая оценка
погрешности:
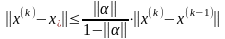 .
.
Запишем это соотношение через начальное приближение , имеем
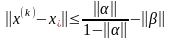 - позволяет произвести
оценку погрешности k
– го приближения.
- позволяет произвести
оценку погрешности k
– го приближения.
На основе оценки осуществляется выход из итерационного процесса по результатам расчета:
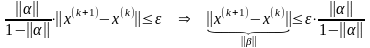 .
.
Запишем
оценку погрешности:
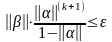 ,
,
тогда из этой формулы получим число итераций требуемых для достижения заданной точности:
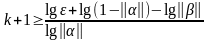 .
.
Методика решения задач.
Преобразовать систему к виду .
Задать начальное приближение решения произвольно либо . Задать малое положительное число ɛ (точно). Положить k=0.
Вычислить следующее приближение
 по формуле
.
по формуле
.Если выполняется условие , то процесс завершить и положить
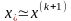 .
Иначе положить k=k+1
и перейти к п.3.
.
Иначе положить k=k+1
и перейти к п.3.
Пример: Методом простых итераций с точность ɛ=0,01 решить систему уравнений:
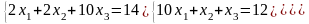
Определить необходимое число итераций.
Решение.
Преобразим систему вида к виду .
Для начала проверим преобладания диагональных элементов, имеем
1
строка:
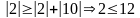 - условие не выполняется,
- условие не выполняется,
2
строка:
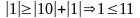 - условие не выполняется,
- условие не выполняется,
3
строка:
 - условие не выполняется.
- условие не выполняется.
С помощью перестановки уравнений в системе приведем систему к виду, где будет выполнено условие преобладания диагональных элементов:

Из
этой системы выразим
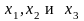 ,
получим систему вида:
,
получим систему вида:
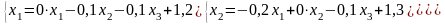 ,
где матрица
,
где матрица
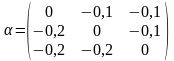 и вектор
и вектор
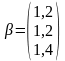 .
.
Найдем
норму
и норму
 :
:
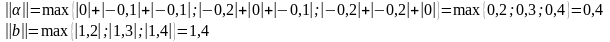
Вычислим число итераций, согласно формуле
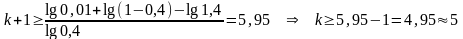 итераций.
итераций.
Зададим начальное приближение
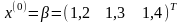 .
По условию ɛ=0,01.
.
По условию ɛ=0,01.Выполним расчет по формуле .
3.1. Положим k=0
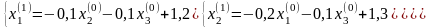
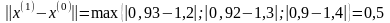 - процесс продолжаем.
- процесс продолжаем.
Расчеты будем заносить в таблицу:
k |
|
|
|
|
0 |
1,2 |
1,3 |
1,4 |
- |
1 |
0,93 |
0,92 |
0,9 |
0,5>ɛ=0,01 |
2 |
1,018 |
1,024 |
1,03 |
0,13>ɛ=0,01 |
3 |
0,9946 |
0,9934 |
0,9916 |
0,0384>ɛ=0,01 |
4 |
1,0015 |
1,00192 |
1,0024 |
0,0108>ɛ=0,01 |
5 |
0,999568 |
0,99946 |
0,9993166 |
0,003084<ɛ=0,01 |
3.2. Положим k=1
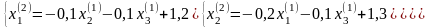
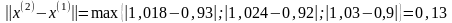 - процесс продолжаем
- процесс продолжаем
3.3. Положим k=2
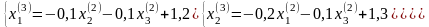
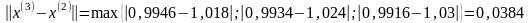 - процесс продолжаем.
- процесс продолжаем.
3.4. Положим k=3
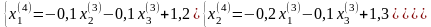
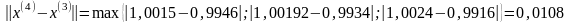 - процесс продолжаем.
- процесс продолжаем.
3.5. Положим k=4
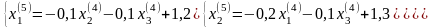
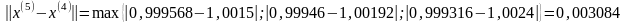 - процесс завершим
и положим
- процесс завершим
и положим