
- •Понятие о численных методах.
- •Погрешности вычислений.
- •3.Задача теории погрешности.
- •3.1. Абсолютная и относительная погрешность суммы и разности приближенных чисел.
- •Абсолютная и относительная погрешность произведения и частного приближенных чисел.
- •Абсолютная и относительная погрешность при вычислении функции нескольких переменных.
- •Контрольные вопросы.
- •Постановка задачи решения слу.
- •Метод простых итераций решения слу.
- •Метод Зейделя решения слу.
- •Методика решения задач.
- •Контрольные вопросы.
- •Постановка задачи решения уравнений. Отделение корней уравнения.
- •Метод половинного деления.
- •Методика решения задачи.
- •Метод хорд решения алгебраических и трансцендентных уравнений.
- •Методика решения задачи.
- •Метод касательных (метод Ньютона) решения алгебраических и трансцендентных уравнений.
- •Методика решения задач методом Ньютона.
- •Основные понятия аналитического приближения табличных функций.
- •Задача аналитического приближения табличных функций.
- •Интерполирование табличных функций.
- •Оценка погрешности полиномиальной интерполяции.
- •Интерполяционный многочлен Лагранжа.
- •5.Интерполяционный многочлен Ньютона.
- •Конечные разности.
- •Первый интерполяционный многочлен Ньютона.
- •Второй интерполяционный многочлен Ньютона.
- •Линейное интерполирование.
- •Формула линейного интерполирования.
ТЕМА №1. ВВЕДЕНИЕ В ПОНЯТИЯ О ЧИСЛЕНЫХ МЕТОДАХ. ОШИБКИ ВЫЧИСЛЕНИЙ.
ПЛАН.
Понятия о численных методах.
Погрешности вычислений.
Задача теории погрешности.
Понятие о численных методах.
Проектирование и обработка современных технических систем связаны с теоретическими расчетами и исследованиями, предваряющими выбор определяющих параметров конструкций. Эти расчеты проводятся с использованием ЭВМ и их систем и вычислительных методов.
При этом выполняются этапы:
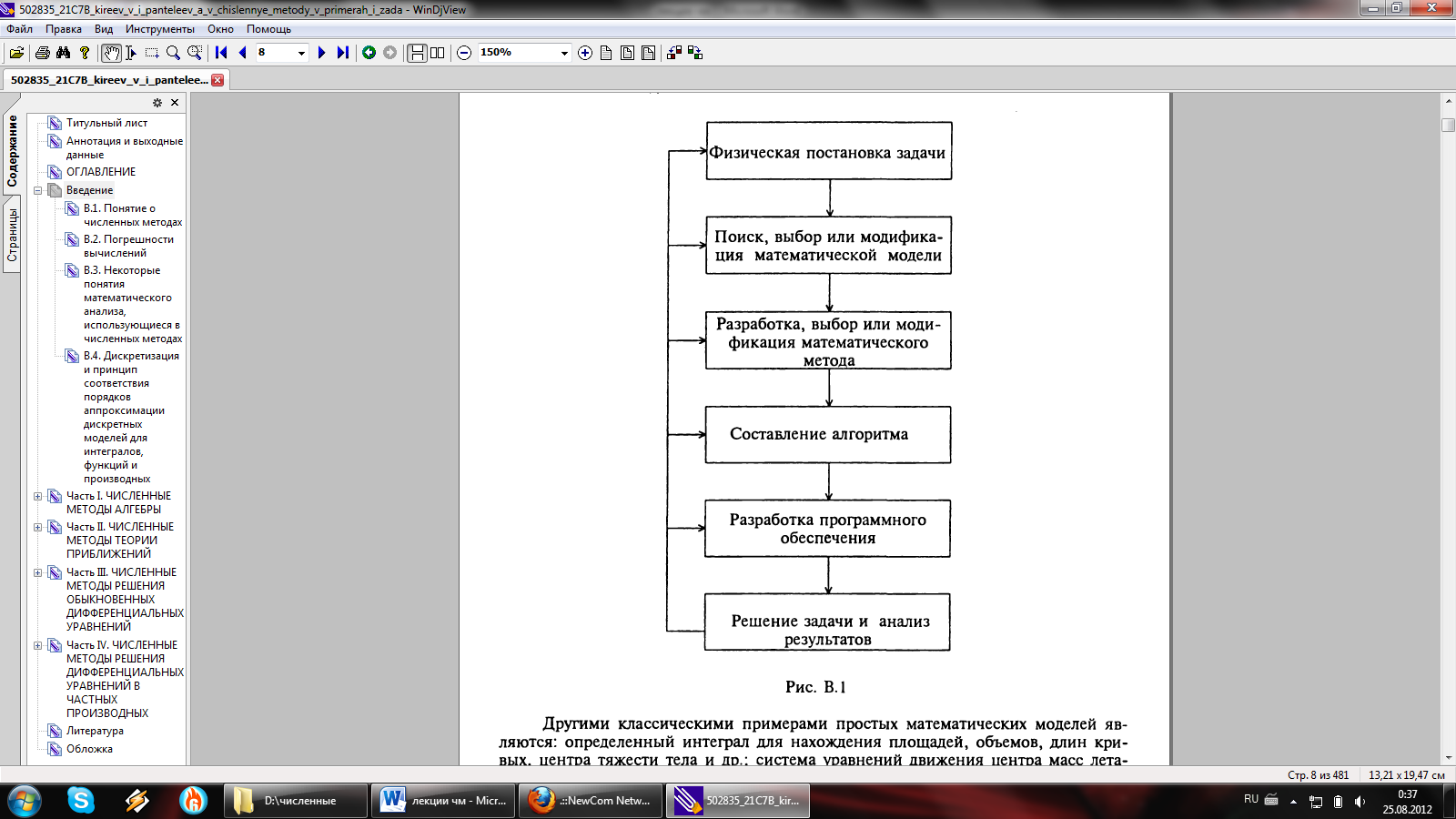
Физическая постановка задачи (результат этого этапа является общая постановка (формулировка) задачи в содержательных терминах).
Поиск, выбор и модификация математического метода: (осуществляется:
запись основных математических уравнений, соотношений, формул, описывающих задачу;
запись дополнительных математических уравнений, связей, граничных и краевых условий;
предварительное обоснование математической модели).
Разработка, выбор или модификация математического метода (осуществляется на основе ресурсов компьютера).
Составление алгоритма
Разработка программного обеспечения.
Решение задач и анализ результатов (обоснование метода и модели путем их методических, параметрических, компьютерных исследований в привязке к реальному объекту).
При решении задачи аналитическими методами («в ручную») получаются точные решения в виде математических формул, а на компьютере приближенные, т.е. задачи широкого класса при обработке современных средств осуществляется численными методами.
Определение: Численные методы – это методы приближенного решения задач прикладной математики, основанные на реализации алгоритмов, соответствующих математическим моделям.
Т.е. численные методы дают не общее, а частичное решение, которое определяется в дискретных областях изменения независимых переменных.
Погрешности вычислений.
Различают два вида погрешностей:
Абсолютная погрешность некоторого числа равна разности между его истинным значением и приближенным значением, полученным в результате вычисления или измерения.
Относительная погрешность – это отношение абсолютной погрешности к приближенному значению числа.
Таким образом, а – точное, но как правило, неизвестное значение величины.
а* - ее известное приближенное значение.
Определение:
Абсолютная погрешность приближения а*
является: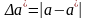 .
Относительной погрешностью приближения
а*
является:
.
Относительной погрешностью приближения
а*
является:
 .
.
Т.к. величина а – неизвестна, при этом необходимо определить погрешность, то вводится придельная относительная погрешность:
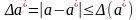
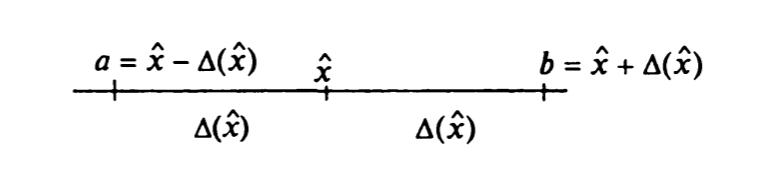
или
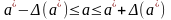 - отрезок которому
принадлежит точное значение а.
- отрезок которому
принадлежит точное значение а.
Т.о. величина а лежит в Δ – окрестности

Придельная
относительная погрешность
а*определяется
отношением: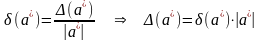
Определение: Значащими цифрами приближенного числа а* называются все цифры в его записи, начиная с первого ненулевого.
Пример: Выделить значащие цифры следующих чисел
2,396037 0,00167 325000 0,00005
Определение: Первые n значащих цифр приближенного числа называются верными, если абсолютная погрешность этого числа не превышает (становится меньше) 0,5 единицы разряда, соответствующего n-ой значащей цифре, считая слева на право. Остальные цифры называются сомнительными.
Пример: выделить верные значащие цифры чисел:
а) х=0,004507, Δ=0,1∙10-4, б) х=12,396, Δ=0,3∙10-1, в) х=9,999785, Δ=0,4∙10-3
Решение.
а) х=0,004507, Δ=0,1∙10-4, n=4 – разряд числа
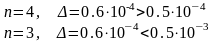
б) х=12,396, Δ=0,3∙10-1, n=5 – разряд числа
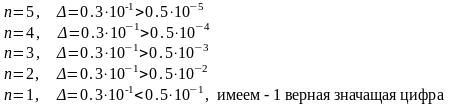
в) х=9,999785, Δ=0,4∙10-3, n=7 – разряд числа
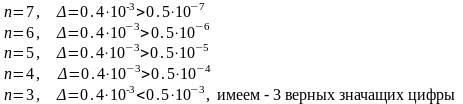
Т.о. возникает вопрос надобности в округлении приближенного числа, т.е. замене его числом с наименьшим количеством значащих цифр.
Замечание: Для округления числа а до n значащих цифр, следует отбросить все его цифры стоящие справа от n – ой значащей цифры.
Правило округления:
Если первая из отброшенных цифр меньше 5, то оставшиеся десятичные знаки сохраняются без изменения.
Если первая из отброшенных цифр больше 5 и среди оставшихся отброшенных цифр есть не нулевые, то к последней оставшейся цифре прибавляется единица.
Если первая из отброшенных цифр равна 5 и остальные отброшенные цифры нулевые, то последняя оставшаяся цифра:
не изменяется, если она четная,
увеличивается на единицу, если она нечетная.
Пример: Найти абсолютную и относительную погрешность числа π=3,141592654…, заданного двумя цифрами после запятой, тремя цифрами после запятой.
Решение.
Найдем погрешность числа π=3,141592654…, заданного двумя цифрами после запятой.
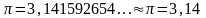
Абсолютная
погрешность:
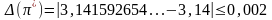
Относительная
погрешность:
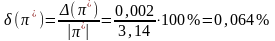
Найдем погрешность числа π=3,141592654…, заданного тремя цифрами после запятой.
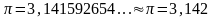
Абсолютная
погрешность:
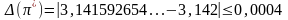
Относительная
погрешность:
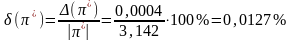 .
.
Замечание: абсолютная и относительная погрешности записываются в виде с одной или двумя значащими цифрами, и они округляются с избытком. В записи приближенных чисел они указываются следующим образом:
 - абсолютная
погрешность
- абсолютная
погрешность
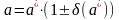 - относительная
погрешность.
- относительная
погрешность.
Т.о. ответ в примере примет вид:
для
округления до числа π с двумя цифрами
после запятой
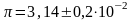 - абсолютная погрешность и
- абсолютная погрешность и
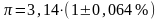 - относительная погрешность. Для
округления числа π с тремя цифрами после
запятой
- относительная погрешность. Для
округления числа π с тремя цифрами после
запятой
 -
абсолютная погрешность и
-
абсолютная погрешность и
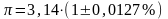 - относительная погрешность.
- относительная погрешность.
