Московский государственный университет печати имени Ивана Федорова

ФИТИМ

Кафедра информатики и вычислительной техники

ДЦасБ-1-1

Типовой расчет

по линейной алгебре и аналитической геометрии

Выполнила: Алпатова М. В.

Проверил: Старинец В.В.

Москва 2012

Теоритические вопросы

1

Формула расстояния между двумя точками

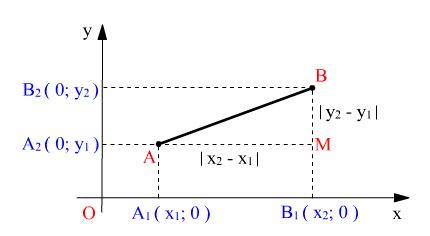
Пусть A и B -- две точки плоскости, координаты которых в декартовой системе координат: (x1 ; y1) и (x2 ; y2 ), тогда   Указанная формула, по существу, является теоремой Пифагора, записанной в координатной форме. В самом деле, пусть A1 и B1 -- соответственно проекции точек A и B на ось абсцисс, M -- проекция A на прямую BB1 . Имеем: AB -- гипотенуза прямоугольного треугольника с катетами AM и BM. но AM = A1 B1 = | x2 - x1|. Тоно так же BM = | y2 - y1 |. Следовательно, AB2 = AM2 + BM2 = (x2 - x1 )2 + (y2 - y1 )2 и формула доказана.

Форумула для нахождения кооординат точки, делящей отрезок в данном отношении

2

Вывод уравнения прямой

Прямую можно задать различными способами. Уравнение

y = kx + b

называется уравнением прямой с угловым коэффициентом k. Любая прямая, не перпендикулярная оси OX, может быть определена этим уравнением. Прямая же, перпендикулярная оси абсцисс, задается уравнениемx = x₀. Отметим, что вертикальная прямая не является графиком функции.

Итак, уравнением y = kx + b можно описать не любую прямую. Этого недостатка нет у так называемого общего уравнения прямой

a x + b y = c      (a2 + b2 ≠ 0).

Если b = 0, то   – получаем уравнение вертикальной прямой. Если же b ≠ 0, то   Таким образом, угловой коэффициент прямой в этой системе обозначений задается как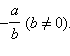 

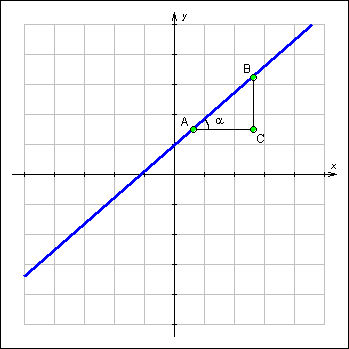
График 2.1.3.2. Угловой коэффициент прямой k = arctg α.

Зафиксируем на графике линейной функции точкуA (x₀; y₀). Пусть B (x; y) – произвольная точка графика. Из треугольника ABC легко увидеть, что  Уравнение

y = y0 + k (x – x0)

называется уравнением прямой с заданным угловым коэффициентом, проходящей через данную точку.

Зафиксируем теперь на графике линейной функции две точки: A (x₁; y₁) и B (x₂; y₂). Из треугольника ABCследует, что   Таким образом, уравнение

задает прямую, проходящую через две заданные точки.

График 2.1.3.3. Уравнение прямой в отрезках на осях

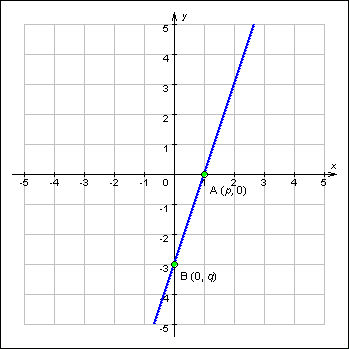
Вернемся теперь снова к общему уравнению прямой a x + b y = c, где a · b · c ≠ 0. Его можно преобразовать к виду   Это уравнение пересекает координатные оси в точках (p; 0) и (0; q).     в чем легко убедиться, подставив координаты этих точек в уравнение прямой. Полученное уравнение называется уравнением прямой в отрезках:

3.