Правила построения эпюр при изгибе (сосредоточенная нагрузка)

1. Для участка, где отсутствует распределенная нагрузка, поперечная сила постоянна, а изгибающий момент меняется по линейному закону, т.е график М_и – наклонная линия.

2. В частном случае, когда поперечная сила на участке равна нулю, изгибающий момент постоянен, график М_и – прямая линия, параллельная оси z.

3. В том месте, где к балке приложена внешняя сосредоточенная сила, на эпюре Q возникает скачок на величину приложенной силы, а на эпюре моментов – излом.

4. В сечении, где к балке приложена пара сил (момент), на эпюре М_и возникает скачок на величину момента. Поперечная сила при этом не изменяется.

5. На конце балки поперечная сила равна приложенной в этом сечении внешней силе.

6. На конце балки М_и равен нулю, за исключением случаев, когда в этом сечении приложен внешний момент. В этом случае М_и равен внешнему моменту.

Построение эпюр q и м (приложены сосредоточенные силы и распределенные нагрузки)

1. Для участка балки с равномерно распределенной нагрузкой поперечная сила Q изменяется по линейному закону, т.е. эпюра Q – наклонная прямая линия.

2. Изгибающий момент изменяется по квадратичному закону, эпюра М_и –парабола, причем, если распределенная нагрузка направлена вниз, то парабола обращена выпуклостью наверх и наоборот.

3. В сечении, где эпюра пересекает ось , т.е Q = 0, М_и – экстремален.

Деформации при чистом изгибе

При чистом изгибе волокна, лежащие на выпуклой стороне бруса, растягиваются, лежащие на вогнутой стороне — сжимаются, а на границе между ними лежит нейтральный слой волокон, которые только искривляются, не изменяя своей длины.

Т. е. при чистом изгибе в поперечном сечении бруса возникают только нормальные напряжения растяжения и сжатия, неравномерно распределенные по сечению.

Искривление волокон и оси бруса происходит за счет неравномерного распределения нормальных напряжений по поперечному сечению.

Линия пересечения нейтрального слоя с плоскостью поперечного сечения называется нейтральной осью. На нейтральной оси нормальные напряжения равны нулю.

НОРМАЛЬНЫЕ НАПРЯЖЕНИЯ ПРИ ИЗГИБЕ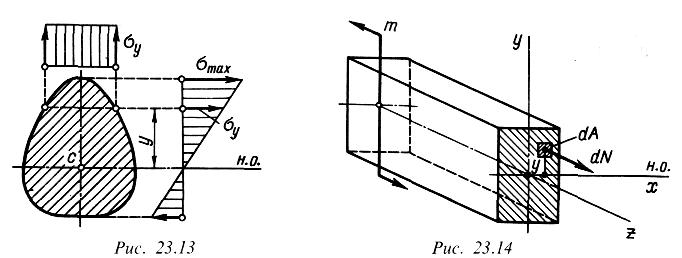

Нормальные напряжения при изгибе распределены по высоте сечения неравномерно: максимальные напряжения возникают в волокнах, наиболее удаленных от нейтральной оси. По ширине сечения нормальные напряжения не меняются.

Нормальные напряжения в любой точке поперечного сечения определяют по формуле: ,

где у – расстояние от нейтральной оси до точки;

I – осевой момент инерции, геометрическая характеристика жесткости сечения при изгибе, мм⁴

Максимальное значение нормальные напряжения будут иметь у волокон, наиболее удаленных от нейтральной оси:

где — осевой момент сопротивления, характеризует влияние формы и размеров сечения на прочность при изгибе, [W] = мм³.

Итак, наибольшие нормальные напряжения при чистом изгибе вычисляем по формуле

 = M / W