2. Осевой момент инерции

Понятие об осевых моментах инерции понадобится нам в дальнейшем при изучении теории изгиба.

• Осевым моментом инерции плоской фигуры относительно оси называется взятая по всей площади сумма произведений площадей элементарных площадок на квадрат их расстояний до этой оси (рис.1).

Осевой момент инерции обозначим I с индексом, соответствующим оси:

; [м⁴, мм⁴].

Сложим моменты инерции относительно двух взаимно перпендикулярных осей х и у (рис. 1.):

, т.е.

• Момент инерции сложной фигуры можно вычислить как сумму моментов инерции простых фигур, на которые разбивают сложную фигуру.

Осевые моменты инерции некоторых простых фигур:

• Прямоугольник b h (рис. 2). ,

Рис.2

• Круг диаметром d относительно осей х и у. В силу симметрии для круга I_Х = I_У. Так как 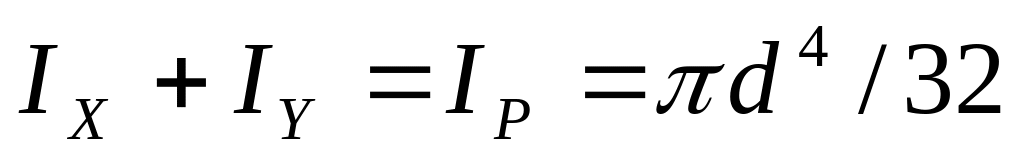, то .

• Осевые моменты для стандартных профилей определяются по справочным таблицам.

  3. Главные оси и главные моменты инерции

Оси, проходящие через центр тяжести фигуры, называются центральными. Момент инерции относительно центральной оси называется центральным моментом инерции.

Оси, относительно которых моменты инерции имеют максимальное и минимальное значения, называются главными осями инерции.

Момент инерции относительной главной оси называется главным моментом инерции.

Если главная ось проходит через центр тяжести фигуры, то она называется главной центральной осью, а момент инерции относительно этой оси — главным центральным моментом инерции. Если фигура имеет ось симметрии, то эта ось всегда будет одной из главных центральных осей.

4. Момент инерции при параллельном перенесении осей

Момент инерции относительно какой-либо оси равен центральному моменту инерции относительно оси, параллельной данной, плюс произведение площади фигуры на квадрат расстояния между осями, т.е (рис.2).

Тема 5. Кручение

Кручением называется такой вид деформации, при котором в поперечных сечениях бруса возникает только крутящий момент (М_К или М _z).

• Крутящий момент в произвольном поперечном сечении бруса определяют методом сечений, он равен алгебраической сумме внешних моментов, действующих на от­сеченную часть: M_k=SM_{i ост. части}.

• Внешние скручивающие моменты определяют по формуле: M = P/w,

где Р — передаваемая мощность, Вт; w — угловая скорость вращения вала, рад/с.

• Внешний скручивающий момент считаем положительным, если он направлен против часовой стрелки.

Напряжения и деформации при кручении

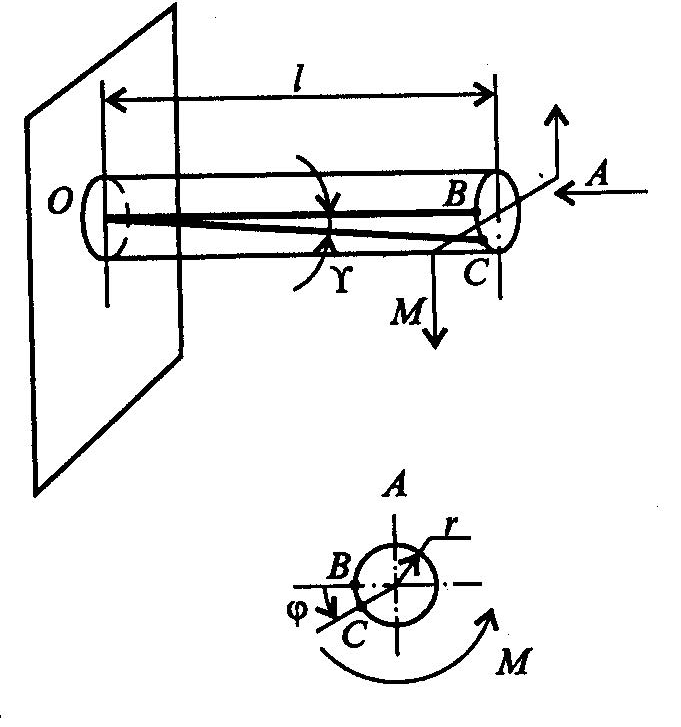
Рассмотрим кручение круглого бруса.

К круглому брycy, жестко заделанному в стену, на свободном торце приложен скручивающий момент М. В результате этого брус деформируется: смежные сечения поворачиваются относительно друг друга, образующая ОВ искривляется и занимает положение ОС.

При описании кручения принимаются следующие допущения и правила:

• ось бруса не деформируется;

• поперечные сечения, плоские до деформации, после деформации также остаются плоскими;

• продольные волокна не изменяют своей длины (угол γ настолько мал, что изменением длины можно пренебречь);

• радиусы r поперечных сечений остаются прямыми после деформации, поворачиваясь на некоторый угол φ, называемый углом закручивания, [рад];

• Существует понятие относительного угла закручивания : φ_о = φ / l, [рад/м] ,

где l – длина бруса.

Таким образом, при кручении в поперечном сечении бруса возникают только касательные напряжения τ.

• Касательные напряжения τ при кручении распределяются по се­чению неравномерно: в центре они равны нулю, а на максимальной окружности поперечно­го сечения - максимальному зна­чению τ_mах. Поэтому расчет ве­дется по τ_mах.

З начение касатель­ного напряжения в любой точке бруса зависит от внутреннего крутящего момента и геометрической характеристики по­перечного сечения: τ = М_к ρ / I_р ,

где ρ – расстояние от данной точки до оси кручения,

J_p – полярный момент инер­ции сечения ( геометрическая характеристика сечения бруса, характеризующая жесткость бруса при кручении).

Полярный момент инерции для сплошного круглого бруса мм⁴

При ρ = r напряжения достигнут максимального значения:

где W_p = I_P / r — момент сопротивления кручению (или полярный момент сопротивления), характеризует прочность бруса при кручении с геометрической стороны.

Единица момента сопротивления кручению [W_p ]= [I_P] / [r] = мм³

τ_mах = М_кmах / W_p,

• Определим момент сопротивления кручению для круглого сечения диаметром d:

• Деформации (φ - углы закручивания, рад) при кручении круглого цилиндра вычисляют по формуле: φ = М_к l / ( GI_p ), где

где I_p — полярный момент инерции сечения;

G — модуль упругости при сдвиге; l – длина участка бруса.

• Построение эпюр. При кручении строят эпюры внутренних силовых факторов (крутящих моментов) и перемещений (углов закручивания φ).