14 Двоякопреломляющие пластинки в полволны и четверть волны.

Рассмотрим кристаллическую пластинку, вырезанную параллельно оптической оси. При падении на такую пластинку плоскополяризованного света обыкновенный и необыкновенный лучи оказываются когерентными. На входе в пластинку разность фаз δ этих лучей равно нулю, на выходе из пластинки

(7);

(мы предполагаем, что свет падает на пластинку нормально).

Вырезанная параллельно оптической оси пластинка, для которой

(nо - ne)d = mλ0+ λ0/4

где m-любое целое число либо нуль, называется пластинкой в четверть волны. При прохождении через такую пластинку обыкновенный и необыкновенный лучи приобретают разность фаз, равную π/2 (напомним, что разность фаз определяется с точностью до 2πm).

Пластинка, для которой

(nо - ne)d = mλ0 + λ0/2,

называется пластинкой в полволны, и т.д.

Рис. 6.5. Прохождение плоско-поляризованного света через пластинку в полволны.

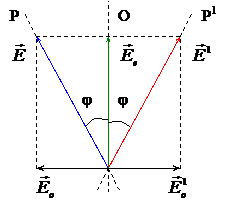
Рассмотрим прохождение плоско-поляризованного света через пластинку в полволны. Колебание в падающем луче, совершающиеся в плоскости Р, возбудит при входе в кристалл колебание обыкновенного луча и колебание необыкновенного луча (рис. 6.5). За время прохождения через пластинку разность фаз между колебаниями и изменяется на p.

Поэтому на выходе из пластинки фазовое соотношение между обыкновенным и необыкновенным лучами будет соответствовать взаимному расположению векторов и (на входе в пластинку оно соответствовало взаимному расположению векторов и ). Следовательно, свет, вышедший из пластинки, будет поляризован в плоскости Р1. Плоскости Р и Р1 расположены симметрично относительно оптической оси пластинки О. Таким образом пластинка в полволны поворачивает плоскость колебаний прошедшего через нее света на угол 2j (j – угол между плоскостью колебаний в падающем луче и осью пластинки).

Рис. 6.6. Прохождение плоско-поляризованного света через пластинку в четверть волны

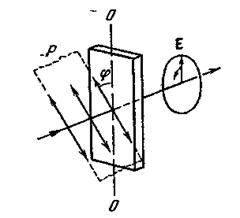Теперь пропустим плоско-поляризованный свет через пластинку в четверть волны (рис. 6.6). Если расположить пластинку так, чтобы угол j между плоскостью колебаний в падающем луче и осью пластинки О равнялся 45°, амплитуды обоих лучей, вышедших из пластинки, будут одинаковы (предполагается, что дихроизма нет). Сдвиг по фазе между колебаниями в этих лучах составит p/2. Следовательно, свет, вышедший из пластинки, будет поляризован по кругу. При ином значении угла j амплитуды вышедших из пластинки лучей будут неодинаковыми. Поэтому при наложении эти лучи образуют свет, поляризованный по эллипсу, одну из осей которого совпадает с осью пластинки О.

15 Эффект Керра заключается в возникновении двулучепреломления поляризованного света, распространяющегося в диэлектрике, помещенном электрическом поле.

Оптически изотропный диэлектрик (твердый, жидкий, газообразный) может стать оптически анизотропным при внесении его во внешнее однородное электрическое поле (эффект Керра). Под действием поля диэлектрик по своим оптическим свойствам становится подобным одноосному кристаллу, оптическая ось которого параллельна направлению поля. Эффект Керра (структурная схема изображена на рис. 3.18) возникает во многих изотропных веществах, но наиболее часто используется нитробензол, который имеет наибольший коэффициент Керра по сравнению с другими веществами (вода, бензол, эпоксидные компаунды и др.).

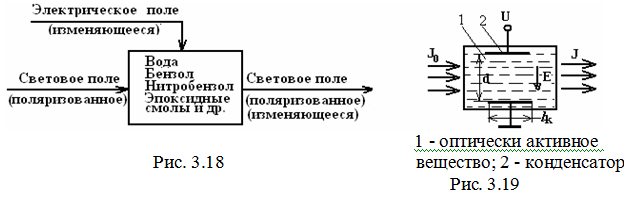
На рис. 3.19 показано устройство ячейки Керра (преобразователя Керра). Электрическое поле в оптически активном веществе 1 создается с помощью двух электродов 2, на которые подается электрическое напряжение U.

ne − no = Bλ0E2,

где λ0 — длина волны света в вакууме; B — постоянная Керра, зависящая от природы вещества, длины волны λ0 и температуры. Для большинства веществ B > 0, что означает их подобие оптически положительным одноосным кристаллам.

Для монохроматического света, распространяющегося в веществе перпендикулярно вектору напряженности внешнего электрического поля , раз-ность хода для обыкновенного и необыкновенного лучей

где k – коэффициент пропорциональности, зависящий от свойств вещества.

Интенсивность света J на выходе ячейки Керра (рис. 3.19) определяется выражением

где J0 – интенсивность света на входе ячейки; Сk – коэффициент Керра; lk – эффективная длина ячейки Керра; d – расстояние между электродами.

Одной из характеристик веществ, в которых наблюдается эффект Керра, является постоянная Керра: К = k/n, где n - абсолютный показатель преломления вещества в отсутствие внешнего электрического поля.

Электрооптический эффект Керра используется для измерения напряженности электрического поля и напряжения. На рис. 3.20 показано устройство вольтметра на основе эффекта Керра.

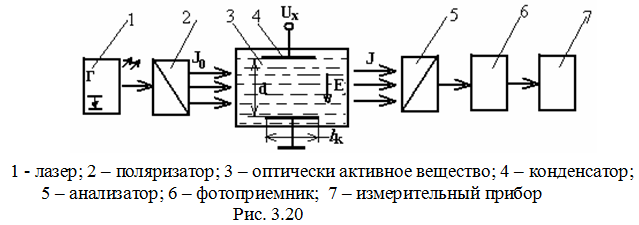
Поляризованный луч света, образуемый с помощью источника света 1 (лазер) и поляризатора 2, проходит через электрическое поле в оптически активном веществе 3, создаваемое конденсатором 4, к электродам которого приложено измеряемое напряжение Ux. При этом луч света направлен перпендикулярно вектору напряженности этого поля. После анализатора 5 свет попадает в фотоприемник 6, где он преобразуется в электрический сигнал, измеряемый прибором 7.

Оптически активные вещества — среды, обладающие естественной оптической активностью. Оптическая активность — это способность среды (кристаллов, растворов, паров вещества) вызывать вращение плоскости поляризации проходящего через неё оптического излучения (света). Метод исследования оптической активности — поляриметрия. Оптически активные вещества подразделяются на 2 типа.

Относящиеся к 1-му из них оптически активны в любом агрегатном состоянии (сахара, камфора, винная кислота), ко 2-му — активны только в кристаллической фазе (кварц, киноварь). У веществ 1-го типа оптическая активность обусловлена асимметричным строением их молекул, 2-го типа — специфической ориентацией молекул (ионов) в элементарных ячейках кристалла (асимметрией поля сил, связывающих частицы в кристаллической решётке).

16 Тепловое излучение и его характеристики. Модель абсолютно черного тела. Все твердые тела, нагретые до высокой температуры, накаляются и начинают испускать видимый свет. Излучение представляет собой электромагнитные волны различных частот. Измерения показывают, что излучение происходит и при более низких температурах. По мере понижения температуры уменьшается интенсивность излучения и меняется распределение излученной энергии по частотам. Излучение, испускаемое нагретыми телами, называется тепловым.

Каждое тело одновременно не только испускает, но и поглощает тепловое излучение. Опытным путем установлено, что чем больше энергии тело излучает при некоторой температуре, тем больше оно поглощает падающую на него энергию, излученную другими телами при той же температуре. Поток энергии Ф (мощность излучения) – количество энергии, излучаемое в единицу времени со всей поверхности тела.

Энергетическая светимость R (интегральная испускательная способность) тела – физическая величина, численно равная энергии, излучаемой в единицу времени с единицы площади поверхности тела (энергия электромагнитных волн всевозможных частот (или длин волн) от 0 до 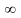). Энергетическая светимость тела связана с потоком энергии Ф выражением:

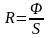, [Вт/М²]

где S – площадь излучающей поверхности тела.

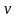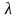Энергетическая светимость тела является интегральной характеристикой, которая не позволяет судить о том, как распределена энергия излучения по различным частотам (или длинам волн). Распределение энергии теплового излучения по частотам (или длинам волн ) характеризуют спектральной плотностью энергетической светимости (испускательной способностью) тела Rv (или R ).

, ;

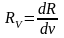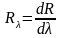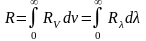
Доля всей падающей энергии в интервале частот от v до v+dv, которая поглощается телом, называется спектральной поглощательной способностью тела Av:

Тело, которое способно полностью поглощать все падающее на него излучение любой частоты, называется абсолютно черным телом. Для абсолютно черного тела Av =1.

Абсолютно чёрное тело — физическая идеализация, применяемая в термодинамике, тело, поглощающее всё падающее на него электромагнитное излучение во всех диапазонах и ничего не отражающее. Несмотря на название, абсолютно чёрное тело само может испускать электромагнитное излучение любой частоты и визуально иметь цвет. Спектр излучения абсолютно чёрного тела определяется только его температурой.

Важность абсолютно черного тела в вопросе о спектре теплового излучения любых (серых и цветных) тел вообще, кроме того, что оно представляет собой наиболее простой нетривиальный случай, состоит еще и в том, что вопрос о спектре равновесного теплового излучения тел любого цвета и коэффициента отражения сводится методами классической термодинамики к вопросу об излучении абсолютно черного (и исторически это было уже сделано к концу XIX века, когда проблема излучения абсолютно черного тела вышла на первый план).

Наиболее чёрные реальные вещества, например, сажа, поглощают до 99 % падающего излучения (то есть имеют альбедо, равное 0,01) в видимом диапазоне длин волн, однако инфракрасное излучение поглощается ими значительно хуже. Среди тел Солнечной системы свойствами абсолютно чёрного тела в наибольшей степени обладает Солнце.