Вопрос 7

Разобьем открытую часть волновой поверхности в плоскости щели MN на зоны Френеля, имеющие вид полос, параллельных ребру М щели.. Так как свет на щель падает нормально, то плоскость щели совпадает с волновым фронтом; следовательно, все точки волнового фронта в плоскости щели будут колебаться в одинаковой фазе. Амплитуды вторичных волн в плоскости щели будут равны, так как выбранные зоны Френеля имеют одинаковые площади и одинаково наклонены к направлению наблюдения.

Из выражения (179.1) вытекает, что число зон Френеля, укладывающихся на ширине щели, зависит от угла j. От числа зон Френеля, в свою очередь, зависит результат наложения всех вторичных волн. Из приведенного построения следует, что при интерференции света от каждой пары соседних зон Френеля амплитуда результирующих колебаний равна нулю, так как колебания от каждой пары соседних зон взаимно гасят друг друга. Следовательно, если число зон Френеля четное, то

и в точке В наблюдается дифракционный минимум (полная темнота), если же число зон Френеля нечетное

, то

и наблюдается дифракционный максимум, соответствующий действию одной нескомпенсированной зоны Френеля. Отметим, что в направлении j=0 щель действует как одна зона Френеля, и в этом направлении свет распространяется с наибольшей интенсивностью, т. е. в точке В0 наблюдается центральный дифракционный максимум.

Вопрос 8

Д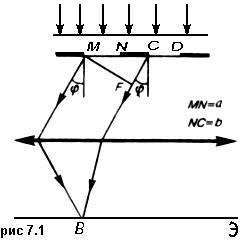 ифракция Фраунгофера на дифракционной решетке. Условия минимумов и максимумов.

Дифракционная картина на решетке определяется как результат взаимной интерференции волн, идущих от всех щелей, т. е. в дифракционной решетке осуществляется многолучевая интерференция когерентных дифрагированных пучков света, идущих от всех щелей.

Рассмотрим дифракционную решетку. На рис. 7.1 для наглядности показаны только две соседние щели MN и CD. Бели ширина каждой щели равна а, а ширина непрозрачных участков между щелями b, то величина d=a+b называется постоянной (периодом) дифракционной решетки. Пусть плоская монохроматическая волна падает нормально к плоскости решетки. Так как щели находятся друг от друга на одинаковых расстояниях, то разности хода лучей, идущих от двух соседних щелей, будут для данного направления φ одинаковы в пределах всей дифракционной решетки:

Таким образом, полная дифракционная картина для двух щелей определяется из условий:

- главные минимумы;

- дополнительные минимумы;

- главные максимум

Вопрос 9

Дисперсия света (разложение света) — это явление зависимости абсолютного показателя преломления вещества от длины волны (или частоты) света (частотная дисперсия), или, что то же самое, зависимость фазовой скорости света в веществе от длины волны (или частоты) Следствие Дисперсия света - разложение в спектр пучка белого света при прохождении сквозь призму

О дной из важнейших характеристик дифракционной решетки является ее разрешающая способность, характеризующая возможность разделения с помощью данной решетки двух близких спектральных линий с длинами волн λ и λ + Δλ. Спектральной разрешающей способностью R называется отношение длины волны λ к минимальному возможному значению Δλ, то есть

Таким образом, предельное разрешение дифракционной решетки зависит только от порядка спектра m и от числа периодов решетки N