2.2 Обозначения теории графов
Граф можно рассматривать как нотацию для бинарного отношения двух множеств. В настоящее время принято определение графа давать в терминах теории множеств.
Графом называется совокупность двух множеств: G=(V, Е), где V={v1,v2, ..., vn} – непустое (обычно счётное) множество вершин графа, а Е={е1, е2, ..., еm} - множество пар вершин (ребер) графа. Числа n и m определяяют мощности множеств вершин и рёбер графа соответственно. Граф называется ориентированным, если рёбра <vi, vj> и <vj, vi> неразличимы; в противном случае граф неориентированный. Рёбра вида <vi, vi> называются петлями. Наглядно вершины графа изображаются точками, а ребра - отрезками прямых линий. Рядом с вершинами и ребрами записывается информация, позволяющая однозначно их идентифицировать и описать их свойства. В частности, числовой характеристикой ребра может быть его длина или вес (в этом случае граф называется взвешенным).
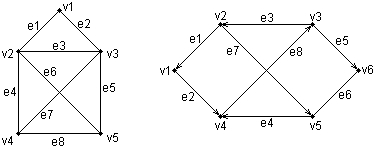
На рис. 2.4 даны два примера графов - .неориентированного (рис. 2.4а) и ориентированного (рис. 2.4б). Иа плоском рисунке изображения некоторых рёбер пересекаются, но точки их пересечений к вершинам граа не относятся.
(а) (б)
Рис. 2.4. Изображения неориентированного и ориентированного графов.
Применение графов характерно для представления информации о структуре процессов и систем. Таковыми служат: схемы телекоммуникаций и автодорог, причинно-следственные связи явлений, схемы алгоритмов и т.п.
Для графов понятие пути (маршрута) отражает последовательные перемещения между вершинами по соединяющим их ребрам. Путь определяется как упорядоченная последовательность ребер S=<el, e2, ..., ek>, где каждые два соседних ребра имеют общую вершину. Ребро el называется началом, а ребро ek - концом маршрута S. Путь можно задать и последовательностью смежных вершин графа S=<vl, v2, ...,vek>. Путь в графе, не включающий повторяющихся рёбер или вершин, называется простой цепью, а путь, начинающийся и оканчивающийся одной и той же вершиной – циклом. .
Граф называется связным (ориентированный – сильно связным), если между любой парой его вершин существует хотя бы один путь. Ориентированный граф слабо связен, если является связным соответствующий неориентированный граф, полученный заменой ориентированных рёбер неориентированными.
Исключительно важную роль в информационных технологиях играют графы специального вида – т.н. деревья. Эквивалентные определения дерева положены в основу различных алгоритмов обработки информации.
Деревом T=<V, E> называют конечный неориентированный связный граф без циклов. Одна из вершин дерева может быть названа корнем, а рёбра дерева обычно называются ветвями. Тогда корень с любой другой вершиной связывает только один путь; в корень не «входит» ни одной ветви, а в любую другую вершину со стороны корня – только одна (это т.н. степень или степень захода вершины.) Аналогичное определение можно дать дереву в ориентированном графе. Ориентированное дерево — ориентированный слабо связный граф без циклов, в котором только одна вершина имеет нулевую степень захода, а все остальные вершины - степень захода 1. При этом корень дерева - вершина с нулевой степенью захода, а вершины с нулевой степенью исхода (без выходящих ветвей) – его листья.
Примеры неориентированного и ориентированного деревьев даны на рис. 2.5.
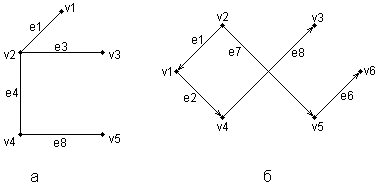
Рис. 2.5. Примеры неориентированного (а) и ориентированного (б) деревьев.
В неориентированном графе дерева (рис. 2.5а) любую вершину можно назначить корнем, что определяется особенностями решаемой задачи. Например, корнем можно назвать вершину v1. Для дерева в ориентированнм графе (рис. 2.5б) только вершина v2 может быть корнем и обозначена v0.
Деревья принято изображать в виде иерархической структуры, когда корень дерева является вершиной уровня 0 (верхнего) и непосредственно связан с вершинами уровня 1, и т.д. Изображенные выше деревья (рис. 2.5) можно преобразовать к виду иерархий. Например, неориентированное дерево (рис. 2.5а) может быть представлено в виде иерархического дерева следующим образом (рис. 2.6а). В этом случае корнем иерархии является вершина v1. Ориентированное дерево (рис. 2.5б) также может быть изображено в форме иерархического дерева (рис. 2.6); такое представление является единственным.
В первом случае первый уровень иерархии представлен вершиной v2, вершины v4 и v3 – лежат на втором, а вершина v5 – на последнем, третьем уровне. Вершины v3 и v5 являются листьями дерева (рис. 2.5а) . На рис. 2.6б вершины v1 и v5 лежат на первом, вершины v4 и v6 – на втором, а вершина v3 – на третьем уровне иерархии;. v3 и v6 – листья.
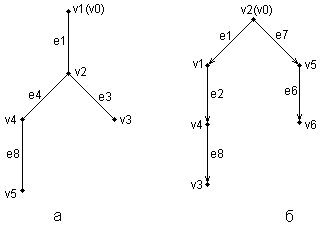
Рис. 2.6. Схемы иерархии неориентированного (а) и ориентированного (б) деревьев
В теории графов разработаны методы анализа различных классов графов и алгоритмы построения специальных графовых объектов, изложенных в многочисленных источниках. Наиболее часто теория графов в информатике применяется для исследования логико-интуитивного описания знаний или при анализе какой либо конкретной предметной области естественного языка и представлении её в виде тезауруса. (см. ГОСТ 7.24—90 "СИБИД. Тезаурус информационно-поисковый многоязычный. Состав, структура и основные требования к построению.).