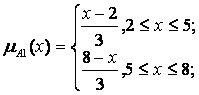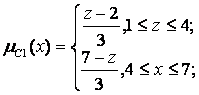6.3. Системы управления с нечеткой логикой

В последнее время системы управления и принятия решений с нечеткой логикой (СНЛ) стали применяться от систем медицинской диагностики до систем компьютерной безопасности. Наиболее эффективно использование СНЛ в плохо формализуемых и трудно структурироемых процессах, управляемых операторами, не имеющими специальных знаний динамики функционирования этих процессов.

В СНЛ вводится опыт эксперта, принимающего решение, т.к. с ростом сложности системы падает способность человека делать точные утверждения о ее поведении, вплоть до достижения порога, когда точность и релевантность становятся взаимоисключающими.

В СНЛ связи между входом и выходом процессов описываются набором правил нечеткой логики (ЕСЛИ-ТО правил), где вместо вместо усложненной динамической модели использоваы лингвистические переменные. Применение лингвистических переменных и правил нечеткой логики, а также приближенных рассуждений дает внести опыт эксперта в схему управления.

Смысл лингвистического значения X характеризуется функцией принадлежности µ: U > [0,1], когда каждому элементу uU соответствует число из интервала [0,1].

Рассмотрим управление беспилотным самолетом. Введем две лингвистические переменные: <дистанция> (расстояние до цели) и <направление> (угол между касательной к траектории движения и направлением на цель). Значениями переменной <дистанция> будут <далеко>, <недалеко>,<близко> и <очень близко>. При физической реализации лингвистической переменной определим точные физические значения термов этой переменной, т.к. расстояние может быть любым от нуля до бесконечности.

В процессе фазификации каждому значению расстояния из указанного диапазона надо сопоставить число от нуля до единицы, определяющее степень принадлежности физического расстояния (допустим, 40 м) к тому или иному терму лингвистической переменной <дистанция>.

Степень принадлежности называемой функцией принадлежности М(d), где d-расстояние до цели. В нашем случае расстоянию 40 м зададим степень принадлежности к терму <очень близко> равную 0,7 , а к терму <близко> – 0,3. Конкретно определить степени принадлежности может только эксперт. См. рис. 6.6.

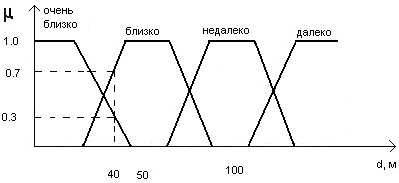
Рис. 6.6. Лингвистическая переменная и функция принадлежности.

Переменная <направление>, имеющая значения от 0 до 360 градусов, получает термы <налево>, <прямо> и <направо>. В этом примере одна выходная переменная <рулевой угол> содержит термы: <резко влево>, <влево>, <прямо>, <вправо>, <резко вправо>. Таблице нечетких правил дана на рис. 6.7.

Рис. 6.8. Таблица нечетких правил.

Каждая запись в таблице соответствует нечеткому правилу; так, если <ДИСТАНЦИЯ БЛИЗКО> и <НАПРАВЛЕНИЕ НАПРАВО>, тогда <РУЛЕВОЙ УГОЛ РЕЗКО ВПРАВО>.

Таким образом, нечеткое управление самолетом будет работать по следующей схеме: данные с сенсоров о расстоянии до цели и направлении на нее фазифицируются, обрабатываются по табличным правилам, дефазифицируются, а результаты в виде управляющих сигналов поступают на исполнительные механизмы самолета.

Применение нечеткой логики в системах ограниченно по следующим причинам:

• у реальных систем управления больше входов, чем у нечетких моделей;

• сложность вычислений экспоненциально зависит от числа входных переменных;

• резко увеличивается и трудно воспринимается база правил.

Структура типичной CHЛ (рис. 6.8) имеет 4 основных блока: входной преобразователь четкой переменной в нечеткую (блок фазификации), база правил нечеткой логики, блок нечеткого логического вывода и выходной преобразователь из нечеткой переменной в четкую (блок дефазификации)

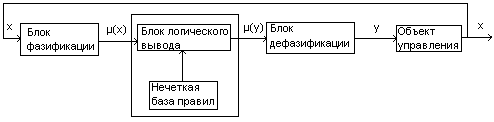
Рис. 6.8. Стандартная структура СНЛ.

Если выходной сигнал блока дефазификации не управляет объектом, СНЛ является системой принятия решения на основе нечеткой логики.

Блок фазификации преобразует измеренные реальных данных (концентрации, плотности, давления и т.д.) в соответствующие значения лингвистических переменных.

В нечеткой базе правил собраны опытные данные о процессе управления и экспертные знания о предметной области, а блок вывода (ядро СНЛ) дает модель процедуры принятия решения. Вывод основан на нечетких рассуждениях для достижения нужной стратегии управления.

Блок дефазификации нужен для выработки четкого решения или управляющего воздействия в по результатам блока вывода.

СНЛ вычисляет значения управляющих переменных по данным наблюдений или измерений переменных состояния управляемого процесса, поэтому правильный выбор переменных состояния управляемого процесса и управляющих переменных объекта управления оказывает главное влияние на качество работы системы. Именно для этого нужен опыт экспертов. Обычно входными сигналами для СНЛ являются состояние объекта, ошибка вычисления состояния, производная и интеграл от ошибки и т.п. По правилам задания лингвистических переменных входной вектор X и вектор выходного состояния Y, которые содержат возможные состояния (или управляющие сигналы) объекта управления, могут быть определены согласно уравнениям 6.1 и 6.2.

X= { Xi, Ui [Tхi (1), …Tхi (j)... Tхi (ki) ] и μхi [ μхi (1), ....…μ хi ( j)…. μ хi (ki)]} 6.1

Y= { Yi, V i [Tyi (1),…Tyi (j) …Tyi (Si) ] и μyi [ μyi (1), ...…,μyi (j)..,... μyi (Si)]} 6.2 ,

где Xi (i= 1, 2, 3,… n) – входные лингвистические переменные создают пространство входов из n нечетких множеств U=U1,U2,...Un, ,например U1 – расстояние, U2 - скорость и т.д. Tхi (j)... – нечеткие переменные.

Yi – выходные лингвистические переменные, образующие пространство выходов из m нечетких множеств V = V1,V2,...Vm, например V1 – торможение, V2 = поворот руля и т.д.

Из (6.1) и (6.2) следует, что характеристика входной лингвистической переменной хi в предметной области Ui есть

T(хi ) = [Tхi (1), …….Tхi (j)... Tхi (ki) ] и μ(хi) = [ μх_i(1), ....…μх_i(j)….μх(k_i)]} ,

где T(х_i ) - множество k_i термов для х_i, т.е. множество имен значений х_i-ой лингвистической переменной, а μ(х_i) множество k_i функций принадлежности этих термов, каждая из которых связана соответственно с каждым из своих термов и определяет область и веса возможных значений терма. Так, если хi означает скорость, то может означать T(хi ) = {Т1 =«очень медленно», Т2 = «медленно», Т3 = «средне», Т4 = «быстро» Т5 = «очень быстро»} - всего k_i термов, в данном примере k_i= 5. В модели беспилотного самолета для терма «расстояние» k_i= 4.

Так же и выходная лингвистическая переменная y_i связана с множеством T (y_i) = [Ty_i (1),…Ty_i (j) ,…Ty_i (Si)] и μ(y_i ) = [ μy_i (1), ...…μy_i (j),... μy _i (S_i)], где S_i - число термов переменной y_i.

Мощность множества термов |T(х_i )| = k_i определяет количество нечетких разбиений входного пространства на подмножества по выбранной степени детализации описания объекта управления, а мощность выходного потока - |T (y_i )| = S_i..

На рис. 6.9. показаны три нечетких подмножества на интервале [-1, +1], где N - отрицательный, Z - ноль, Р - положительный;

Рис. 6.9. Графическое представление нечеткой декомпозиции:

Количество разбиений входного нечеткого множества для задачи управления определяет максимальное число правил нечеткой логики. Правильный выбор нечеткой декомпозиции входного, выходного пространств и функций принадлежности определяют успех при проектировании СНЛ.

Блок фаззификации преобразует четкие значения входных переменных в нечеткие, что является нормировкой, переводящей измеренные данные в субъективные оценки. Она определена как отображение наблюдаемых значений входных переменных в соответствующие нечеткие. В реальных СНЛ входные данные обычно являются четкими (хотя не исключена погрешность измерения).

Пусть система имеет одну переменную X. Тогда можно определить, что функция принадлежности µ А(х) будет равна 1 в точке х0 и нулю в остальных точках. В данном случае значение x_i(t) в любой момент времени t отображается на нечеткое множество T¹х_i со значением μх_i (t).

База правил нечеткой логики. Правила нечеткой логики заданы набором нечетких конструкций «ЕСЛИ - ТО», где в предпосылки и заключения входят лингвистические переменные. Такой набор управляющих правил (нечетких управляющих утверждений) описывает связь входа и выхода системы. Дадим общую форму правил нечеткой логики для СНЛ с множеством входов и одним выходом (MISO — «multi-input-single-output»):

Ri : ЕСЛИ х ЕСТЬ A_i,...,И у ЕСТЬ Вi ТО z = C_i, i =1,2,…n , (6.3)

где х,...,у и z- соответственно лингвистические переменные для переменных состояния управляемого процесса и управляющие переменные;

Ai,..,Bi и Сi - соответственно лингвистические значения переменных х,...,у и z в предметных областях U,...,V и W.

В другой форме представления правил нечеткой логики заключение есть функция переменных состояния управляемого процесса х,...,у, т.е.

Ri : ЕСЛИ х_i ЕСТЬ A_i,...,И у ЕСТЬ В_i ТО z = f(x,…y), i = 1,2,…n, (6.4)

где f - функция переменных х,...,у состояния управляемого процесса.

В обеих формах входные переменные имеют лингвистические значения, а выходные - лингвистические значения или суть функции переменных состояния управляемого процесса f(x,…y).

Напоминим. что в операциях пересечения нечетких множеств ( использование связки «И») нахождят минимум μ - функций принадлежности нечетких множеств термов, входящих в правила логики через союз И, а затем вычисляют выходные переменные. Полученные значения функций выходных переменных объединяют, т.е. находят максимум этх функций

По уравнениям (6.3) и (6.4) можно получить состояние процесса (интегральную ошибку состояния, ошибку определения состояния, и т.д.) в момент времени t и далее принять решение об управляющих воздействиях в виде функции переменных состояния процесса (х,...,у).

Блок вывода - ядро СНЛ, нужное для моделирования приближенных рассуждений и процесса принятия решений.

Определим понятие отношения для организации нечетких выводов. Пусть знание эксперта отражает нечеткое отношение предпосылки А и заключения В, которое называется нечетким R: R = A→B.

Почти все прикладные системы, использующие промежуточные нечеткие оценки, основаны на нечетких продукционных правилах. Для получения нечетких выводов используют нечеткие отношения R, заданные между областями (множествами) Х и Y в виде нечеткого подмножества прямого (декартова) произведения X Y, обычно определяемого как:

R = ∩ ∩{μR(x_i, y_j) │ (((x_i, y_j))}, i= 1…n, j=1…m (6.5)

где X = {х1,х2,...,хn} - область посылок (входные переменные);

Y = {у1,у2,...,уm} - область заключений;

μR(xi, yj)— функция принадлежности (xi, yj) нечеткому отношению R, знак ∩ означает пересечение совокупности множеств (максимум всех μR(xi, yj)), а μR(xi, yj) Є [0,1] .

Например, если в системе есть два датчика, описываемых лингвистическими переменными А и В c областями рассуждений X и Y соответственно. Пусть X в момент времени t₀ принимает значение X0, Y → Y0, а А и В определены соответственно тремя термами А1, А2, А3 и В1, В2, В3.

Декартово произведение входных переменных приводит к 9 элементам:

(А1, В1),(А1, В2),(А1, В3),

(А2, В1),(А2, В2),(А2, В3),

(А3, В1),(А3, В2),(А3, В3).

Соответственно, выходные переменные - С11,С12,С13,С21,С22,С23,С31,С32,С33, и надо сформулировать 9 правил логики:

ЕСЛИ А=А1 И В =В1, ТО В=С11

ЕСЛИ А=А1 И В =В2, ТО В=С12

ЕСЛИ А=А1 И В =В3, ТО В=С13

ЕСЛИ А=А2 И В =В1, ТО В=С21

ЕСЛИ А=А2 И В =В2, ТО В=С22

ЕСЛИ А=А2 И В =В3, ТО В=С23

ЕСЛИ А=А3 И В =В1, ТО В=С31

ЕСЛИ А=А3 И В =В2, ТО В=С32

ЕСЛИ А=А3 И В =В3, ТО В=С33

Если ненулевые термы лишь А1, В1, А2 и В2, то при вычислении логического вывода надо учесть приниматься первые 2 правила для значений С11, С22.

Для наглядности проведем рассмотрение только с использованием этих термов и назовем С11, С22 как С1, С2. Тогда функции принадлежности треугольного типа μ, точки X0, Y0 приведены на рис. 6.10.

Рис. 6.10. Иллюстрация нечеткого вывода по Мамдани.

Очевидно, μА1(X₀) > μВ1(Y₀ ), а μА2(X₀) < μВ2(Y₀ ). С учетом правил 1, 5 получим:

А1(X₀)∩В1(Y₀ ) = MIN {μА1(X₀) , μВ1(Y₀ )}= μВ1(Y₀ )

А2(X₀)∩В2(Y₀ ) = MIN {μА2(X₀) , μВ2(Y₀ )}= μА2(X₀)

Вычисление μС1, μС2 может осуществляться по-разному; больше распространены методы Ларсена и Мамдани При изложении примера с сушилкой использовался метод Мамдани. Рассмотрим сначала получение вывода по Мамдани на примере с сушилкой.

В этом методе текущие значения (при X₀ и Y₀) функций принадлежности С1(Z,X₀,Y₀) И С2(Z,X₀,Y₀) получают пересеченем функции принадлежности треугольной формы термов С1(Z) И С2(Z) с вычисленными значениями μВ1(Y₀ ) и μА2(X₀), т.е.

С1(Z,X₀, Y₀ ) = А1(X₀)∩В1(Y₀ ) ∩ С1(Z)

С2(Z, X₀, Y₀) = А1(X₀)∩В1(Y₀ ) ∩ С2(Z) , где Z – область рассуждений С1 И С2.

По определению это :

С1(Z, X₀, Y₀) = MIN { С1(Z) [MIN {μА1(X₀) , μВ1(Y₀)]} и

С2(Z, X₀, Y₀) = MIN { С2(Z) [MIN {μА2(X₀) , μА2(Y₀)]}.

На рис. 6.11.видно, что пересечения функций - констант μВ1(Y₀ ) и μА2(X₀) с С1(Z) и С2(Z) образуют две трапеции.

Рис. 6.11. Пересечение функций в методе Мамдани.

Для иллюстрации метода Ларсена введем операцию умножения лингвистических переменных следующими образом.

Пусть F и G - нечеткие множества с функциями принадлежности - μF и μG, тогда H = F • G, если μh = μF • μG.

Тогда, если одна из функций - константа меньше 1 на всей области рассуждений, например μG = s < 1, а μF на всей области рассуждений треугольной формы с максимумом равным 1, то их произведение есть функция принадлежности тоже треугольной формы с максимумом μG = s. Операция умножения как бы сжимает исходную функцию μF с коэффициентом μG = s.

В методе Мамдани конечная операция вычисления выходных лингвистических переменных есть пересечение функций принадлежности их термов с вычисленными значениями входных лингвистических переменных в заданный момент времени. Суть метода Ларсена состоит замене этой операции операцией умножения и геометрически это дает сжатие треугольных функций термов выходных переменных μС_i (рис. 6.12).

Рис. 6.12. Иллюстрация нечеткого вывода по Ларсену.

Дефазификация. Процедура нужна для сопоставления по функции принадлежности μС(Z) числовых значений каждой точке в Z. Сейчас нет систематической процедуры выбора стратегии дефазификации. Обычно используют метод центра тяжести (ЦТ) и метод максимума (ММ). Второй дает лучшие результаты для переходного режима, а ЦТ - в установившемся режиме из-за меньшей среднеквадратичной ошибки.

В дискретном методе ЦТ четкое значение выходной переменной вычисляют как:

∑ Z _j μСj(Z _j)

Zцт = ────────────────── , при J= 1….N,

∑ μС_j(Z _j)

Для непрерывных пространств формула содержит интегральное выражение.

По методу ММ определяют все z, где функции принадлежности достигли максимума. При этом для дискретного варианта получим

∑ Z _j

ZMM= ─── , при J= 1….m, (6.6.),

m

где m – количество целочисленных значений z, где функции принадлежности максимальны, а Zj - j-ое такое значение Z.

Из полученных функций выходных переменных c1 и c2 (трапеций или треугольников, рис. 6.11. и 6.12) результирующая функция получается объединением. На рисунке это получают прорисовкой контура двух исходных фигур c1 и c2, наложенных на области определения (размышления). Для этой функции по приведенным формулам вычисляют центр тяжести или максимум числовых значений для точки в Z(t) в любой момент времени t.

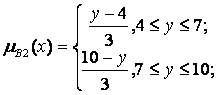
Приведем ример использования СНЛ для нечеткого вывода по Мамдани. Пусть в СНЛ с правилами нечеткого управления:

Правило 1: если x есть A1 и у есть В1 тогда z есть С1;

Правило 2: если x есть A2 и у есть В2 тогда z есть C2.

величины х0 и у0 от датчика - четкие входные величины для лингвистических переменных х и у, и заданы функции принадлежности для нечетких подмножеств А1,А2,В1,В2,С1,С2 этих переменных:

Рис. 6.13. Функции принадлежности для нечетких подмножеств А₁,А₂,В₁,В₂,С₁,С₂

Проиллюстрируем вычисление выходного сигнала, если в момент времени t1 были считаны значения датчиков х0(t1)=4 и y0(t1)=8.

Сначала находят срезы для первого и второго правила по заданным функциям принадлежности и с учетом значений х0 к у0. Для этого вычисляют величины функций принадлежности в заданных точках для первого и второго правил:

(x0=4)=2/3 и (y0=8)=1; (x0=4)=1/3 и (y0=8)=2/3.

Затем по правилу вывода Мамдани выбирают минимальное значение функций принадлежности:

С1(t1) = min((x0), (y0)) = min(2/3, l) = 2/3;

С2(t1)  = min((x0), (y0)) = min(1/3, 2/3) = 1/3;

Результаты для правила 1 (для С1) и правила 2 (для С2) показаны на рис. 6.13.

Рис. 6.14. Иллюстрация нечеткого вывода по Мамдани.

Для вычисления выходной величины z дефазифицируют нечеткую величину. По методу центра тяжести получаем

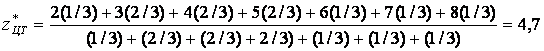(6.7.)

По методу ММ ищут точку z, где µz максимально. Максимум в методе Мамдани обычно плоский и приближенно находят его среднее положение. Для этого подсчитаем число целочисленных значений z, при которых было достигнуто максимальное значение функций принадлежности. На графике максимум 2/3 (вершина одной из трапеций) достигается только при целых значениях z — 3, 4 и 5. Среднее положение максимума µz

Z_MM = (3 + 4 + 5) /3 =4,0 (6.8.)