Оптимизация размещения управляющих серверов в распределенных информационных системах на основе решения задачи о минимальном вершинном покрытии: постановка задачи и точный метод решения

Цель работы – разработка математической модели и метода для решения задачи выбора оптимального размещения серверов в распределенной вычислительной системе для обеспечения максимальной функциональной мощности при заданной оперативности управления и заданной оперативности решения задач на основе задачи о минимальном вершинном покрытии [1].

Задачи определения минимальных вершинных покрытий и максимальных независимых множеств имеют широкое прикладное значение при построении сложных систем, автоматизированных систем управления, разработке программного и математического обеспечения вычислительных систем и сетей. На первый взгляд кажется, что проста, которую можно, например, решить последовательным перебором независимых множеств с одновременной проверкой каждого множества на максимальность (последнее может осуществляться путем добавления к исследуемому множеству дополнительной вершины, не принадлежащей ему, и выяснения того, сохраняется ли при этом независимость) и запоминанием максимальных множеств. Однако с увеличением числа вершин этот способ становится весьма громоздким, на основе усовершенствования этой процедуры построены алгоритмы Брона и Кэрбоша. Задача о минимальном вершинном покрытии является NP-полной и эффективные алгоритмы ее решения для произвольных графов неизвестны. Формализация задачи определения вершинных покрытий сводится к следующей: пусть задан произвольный граф G=(V,E) с множеством вершин {vi}V и ребер Е. Поставим в соответствие каждому ребру {vi,vj} E графа G=(V,E) дизъюнкт (vivvj) с двумя переменными. Тогда нетрудно показать справедливость следующей теоремы.

Теорема. Если f – булева функция, построенная по графу G=(V,E) в виде произведения дизъюнктов (vi v vj), где {vi}{0,1}, , , ij и при этом каждый дизъюнкт (vivj) соответствует ребру (vi,vj), то все наборы переменных {vi,vj}, на которых она принимает значение «истинно», соответствуют вершинным покрытиям в графе G=(V,E).

Из данной теоремы вытекает следующее важное следствие:

Следствие. Для перечисления всех вершинных покрытий графа G=(V,E) необходимо определить те системы значений переменных {vi,vj}, при которых высказывание

f(V1,V2…Vn) = 1,

(1)

«истинно». Чтобы найти эти системы значений переменных {vi,vj}, необходимо привести левую часть (1) к минимальной ДНФ (дизъюнктивной нормальной форме), раскрывая скобки и пользуясь законом поглощения. Такая форма единственна ввиду отсутствия в (1) логических отрицаний.

Покажем это на примере графа G, приведенного на рис. 1.

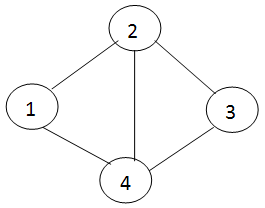
Рис. 1. Граф G

Булева функция для этого графа будет иметь вид:

= = = .

(2)

Как видно из (2), в результате раскрытия скобок и приведения подобных, получаем полный перечень вершинных покрытий графа G (рис. 1). Ими являются подмножества вершин: {2,4}; {1,2,3}; {1,3,4}.

Для экспериментального исследования точного метода и его характеристик, определяющих возможности его применения для решения задач управления и планирования, разработана программа на языке С#. Получены результаты статистического моделирования и проведен их анализ.

Список литературы: 1. Листровой С.В. Метод решения задачи определения минимальных вершинных покрытий и независимых максимальных множеств / С.В. Листровой, С.В. Яблочков // Электронное моделирование. – 2003. – Т.25. – №2. – С. 31 – 43.

УДК 004.778

С.Ю. Дмитренко, студентка 3 курса

svetadmitrenko1@rambler.ru