21Поисковая оптимизация
Большинство
методов предназначено для поиска
локальных экстремумов без учета
ограничений. Поэтому важное значение
приобретает выбор начальной точки
поиска
Локальные методы безусловной оптимизации делятся на:
1) Методы нулевого порядка, в них не используется информация ЦФ. (Методы одномерного поиска: деления отрезка пополам; Методы многомерного поиска- покоординатного спуска; случайного поиска)
2) Методы первого порядка (Градиентный), используется значение ЦФ и первых частных производных по параметрам ( методы градиента; наискорейшего спуска и т.д.)
3) Методы второго порядка, используют значение ЦФ и первых и вторых частных производных (Метод Ньютона)
22Метод покоординатного спуска.
Алгоритм:
1)
из текущей точки поиска выполняется
пробный шаг в положит направлении одной
из координатной осей
,
k-номер
шага поиска. Оценивается улучшение
целевой ф-ии
.
Если это условие выполняется,то это
направление выбирается для дальнейшего
поиска экстремума.В противн.случае
исследуется отрицат направление вдоль
оси,т.е.выполняется пробный шаг
,
2)
выполняется движение вдоль выбранного
направления
до тех пор, пока выполняется условие
3)те же действия выполняются для всех остальных параметров оптимиз-и
4)если из полученной
точки нельзя улучшить целевую ф-ию ни
покакому парам-ру,тоуменьшают шаг
оптимизации:
2)
операции 2-4 повторяют до тех пор пока
23Метод градиента.
1)-в
текущей точке поиска находится градиент
целевой ф-ии:
.Рассчитывается единичный вектор направления:
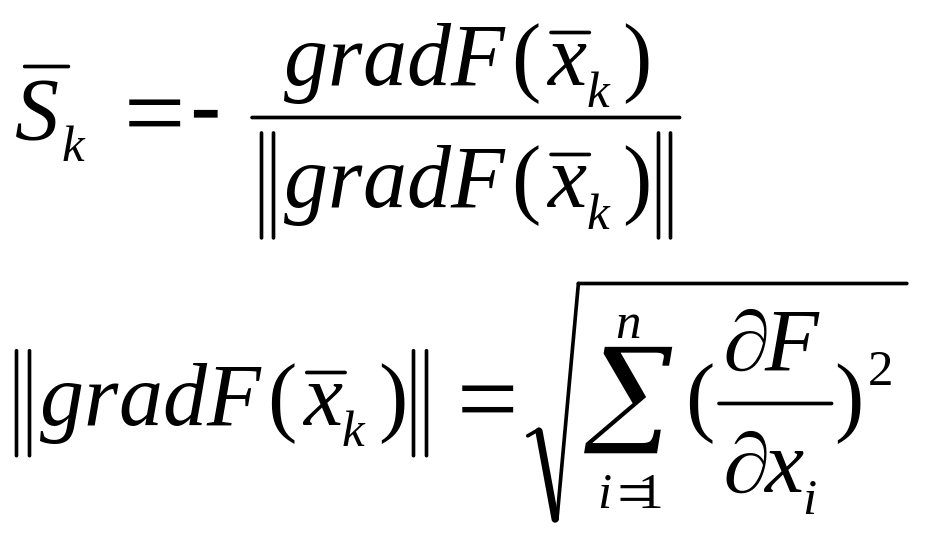
2)-выполняется шаг
поиска
Оценивается успешность поиска.Если
,то
в полученной точке определ-я нов
направление и алгоритм повторяется.В
противном случае уменьшается шаг:
3)-условие окончания поиска
24М-ды мат программирования.Задача линейного программирования
Линейное программ-е связано с исследованием и решением задач:дана сис-ма m линейно независ. ур-й с n неизвестными,наз-я сис-ой ограничений.
Требуется найти неотрицат знач-е переменных,обращающее в min целевую ф-ию(xi>=0):
(1)
наз линейной
формулой и
удовлетвор ограничению(1)
Базисом наз любой набор из m переменных таких,что определитель составленный из коэф-ов при этих переменных не равен нулю.Остальные (n-m)переменных наз свободными.Решение сис-мы ограничений путём приравнивания к нулю свободных переменных наз базисным.Базисное решение,кот удовлетворяет неравенству xi>0,наз допустимым.Решение задачи оптимизации лежит среди допустимых базисных решенй.