13Построение модели на основе пассивного эксперимента. Расчёт доверительных интервалов для коэф-ов ур-я регрессии.Проверка адекватности регрессионной модели

После построения мат модели в виде ур-я регрессии выясняется значимость коэф-ов ур-й и адекватность полученной модели.Для модели рассчит.остаточная дисперсия: ,где Nв-кол-во коэф-ов в регрессии,yi-знач ф-ии отклика по рез-ам эксперимента, -знач ф-ии отклика по расчётам модели.

Остаточная дисперсия м.б. использована как оценка дисперсии ошибки эксперимента:

По критерию Стьюдента определяем значимость коэф:

Далее находиться табличное значение коэфф. Стьюдента: Если рассчитанное значение больше табличного, то считается что коэффициент значимый.

Для значимых коэфф. можно рассчитать доверительный интервал:

Проверка адекватности модели проводиться по критерию Фишера.Опред средн дисперсией:

, -средн знач-е отклика по результатам

Находим наблюдаемое знач-е критерия Фишера: 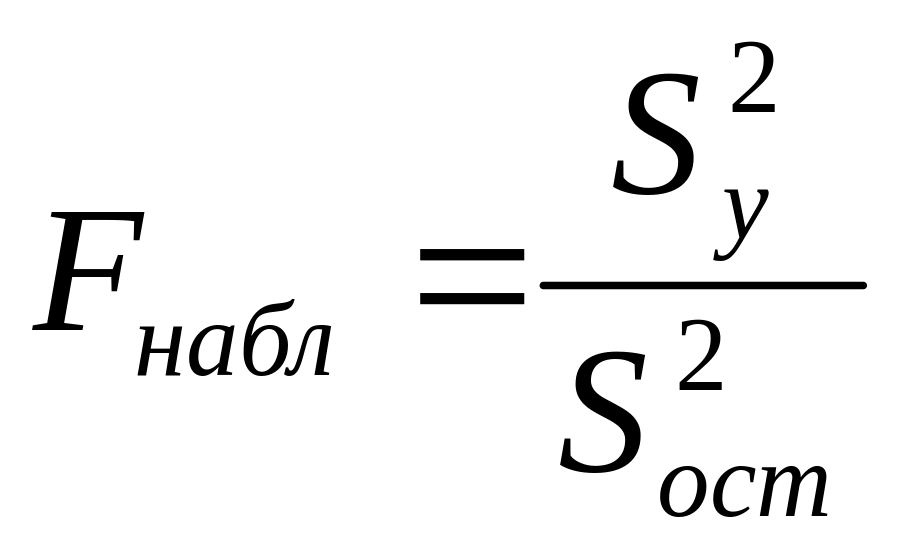. Расчетное значение критерия Фишера сравнивается с табличным. Если расчетное больше табличного, модель считается адекватной.

17Сущность оптимизации.Параметры оптимизации.Критерий оптимиз-и.Целевая ф-я.

Оптимизация заключается в нахождении оптимальных условий проведения данного процесса. Для оценки достижения оптимума, прежде всего, выбираются критерии оптимизации. Это некоторая численная характеристика исследуемого объекта. На основании этого критерия строится целевая функция (функция качества). Задача оптимизации заключается в поиске параметров, при которых целевая функция достигает экстремальных значений - оптимальный параметр. Целевая функция может содержать множество параметров , часть из которых являются управляемыми. Этими параметрами можно варьировать для поиска их оптимального значения. Остальные параметры не подлежат оптимизации. Управляющие параметры м.б. как непрерывные так и дискретные.Если экстремум целевой функции отыскивается в неограниченной области, его наз . безусловным экстремумом, а методы его поиска - безусловной оптимизацией.Целевая ф-я-представляет собой зависимость критерия оптимизации от параметров,влияющих на его значение.

19М-ды оптимизации. Аналитический м-д поиска экстремума

Классификация методов оптимизации:

1)Аналитические методы (аналитический поиск экстремума, метод множителей Лагранжа, вариационные методы)

2) Методы мат. программирования:

а) Геометрическое - используется при оптимизации ЦФ в виде полиномов.

б) Линейное - оптимизация моделей с ЦФ и ограничениями в виде линейной функции.

3)М-ды поисковой оптимизации(м-д градиента, м-д наискорейшего спуска)

Аналитические методы:

В классическом подходе необходимыми условиями локального экстремума явл.

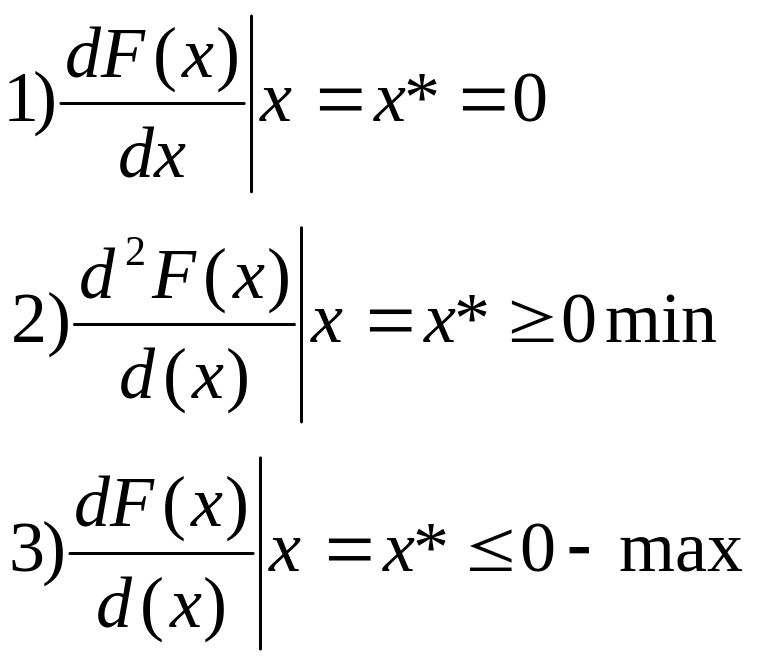
20Метод множителей лагранжа

Метод множителей ЛАГРАНЖА применяется для нахождения оптимальных значений параметра , если на модель наложено ограничение в виде равенств. В этом случае задача оптимизации ставится так: необходимо найти оптимальные параметры модели если ЦФ задана в виде

и заданы ограничения в вида .

Для решения этой задачи составляется ф-я Лагранжа:

,

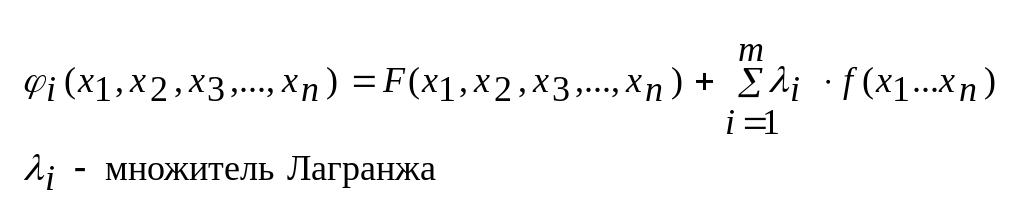В этом случае экстремальные точки ф-ии определяются реш-ем сис-мы ур-й,получаемой приравниванием нулю производных от ф-ии по всем независимым переменным xk(k=1,…n) и по всем множителям Лагранжа .Получаемая сис-ма ур-й:

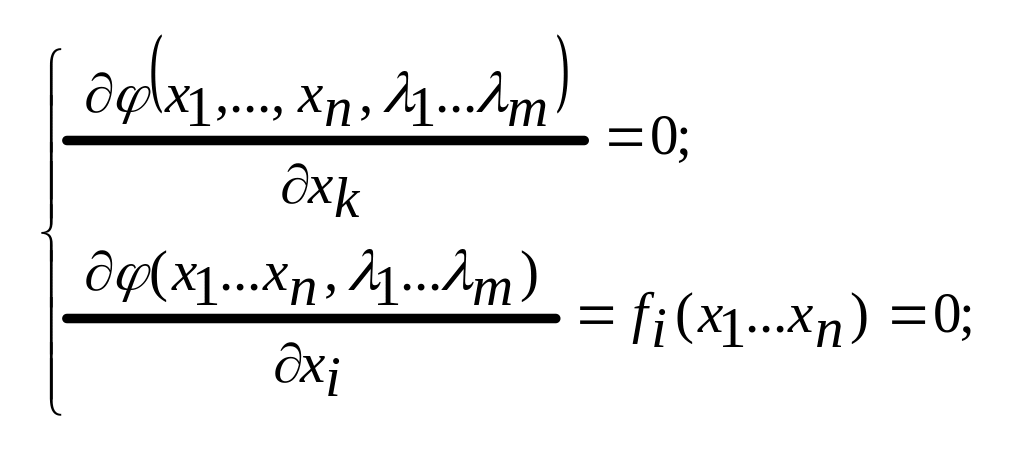
содержит уравнений,из кот можно исключить m неопределённых множителей Лагранжа и найти координаты экстремальных точек xk(k=1,2…n)