9Составление модели экспериментальным статическим путем. Постановка задачи планирования эксперимента. Пассивный и активный эксперимент.Принципы планирования

Эксперимент - целенаправленно организованный опыт, содержащий наблюдение исследуемого явления в специально заданных условиях.Входн параметры x наз факторами,вых параметры наз откликом.

Изучение ф-ния объекта основывается на анализе внешних воздействий X и соотв. им реакции системы Y. Связь м/у X и Y представляют в виде уравнений.

Различают:

1.В пассивном эксперименте значениями факторов управлять нелбзя.Уровни факторов принимают случ.значения.

2.Активный эксперимен-значения факторов задаются и поддерживаются неизменными на опред уровне.

Цель планирования эксперимента-пролучение max информации об исследуемом объекте при min кол-ве опытов

Используются след. принципы:

1.Отказ от полного перебора всех возможных состояний объекта

2.Постепенное усложнение структуры модели

3.Сопоставление рез-ов экс-та с величиной случ.помех

4.Принцип рандомизации опыта.Опыты проводятся таким образом,чтобы все переменные носили случ хар-р

5.Оптимальное планирование экс-та

10Корреляционный анализ

По результатам проведения экс-та проводят корреляц.анализ, рассчит-ся коэф-т корреляции для каждой пары факторов и для факторов и ф-ии отклика

где XiXj-этоi ,j факторы или I -фактор иj-ф-я отклика

SiSj-среднеквадратич отклонения

Xi-значение i-го фактора

N-кол=во опытов в экспероименте

-средн.значение фактора

Если коэф. =1 или -1, то это значит что м/у параметрами сущ.тесная связь. Если =0, то связь отсутствует. Если”0”,то фактор исключается из модели;если1,-1 исключаютфактор менее связанный с входн параметрами

11Регрессионный анализ

Задача анализа-определение параметров экспериментальных факторных моделей

3 этапа:

1.статистич анализ рез-ов экс-та

2.получение коэф-ов регрессионной модели

3.оценка адекватности и работоспособности получ модели

Факторную модель м. представить в след виде:

,φ-ур-е регрессии,x-факторы,b-коэф-ты ур-я регрессии

Результаты экс-та представлены в виде

,ε-аддитивная помеха с норм. з-ом распред-я

Т.к.в рез-те проведения экс-та всегда получаются случ.значения ф-ии отклика,то и рассчитанные знач-я коэф-ов модели b явл-ся оценками истинных значений коэф-ов модели β. Ф-ю φ(x)м. представить:

, βj-коэф ур-я регрессии,f()-j базисная ф-я

Предпосылки:

1.аддитивн помеха ε- случайная нормально распред вел-на с нулевым мат ожиданием и пост дисперсией

2.знач-е факторов в активном экс-те-это не случайн6ые величины

3.знач-е факторов в пассивном экс-те-случайные нормально распред-е велшичины

4.помехи в различных точках опыта не коррелированны

5.вектор-столбы базисных ф-ий, образованных значениями базисных ф-ий в кажд опыте должны быть линейно независимыми

12Оценка параметров регрессионной модели

Исходными данными для оценки параметров регресс модели явл-я данные о значениях факторов x и ф-ии отклика Y. Это информация представлена в виде:

n-кол-во факторов,N-кол-во опытов,Xij-знач-е j фактора в I опыте

. Значения базисных ф-ий в кажд опыте образуют матрицу базисных ф-ий:

fik-знач-е коэф-в в i опыте

Необходимо определить значение вектора . В кажд опыте знач-е ф-ии отклика можно представить в виде (ε-невязка).Для определения параметров модели невязку необход минимизировать для чего используется м-д наименьших квадратов.Составляется ф-я, представ собой сумму квадратов невязок: . Значение коэф-ов b находится таким образом,чтобы эта ф-я приняла min знач-е

Коэф-ты при неизвестных переменных b образуют матрицу Ф:

Ф= ( -матрица базисных ф-ий)

Ф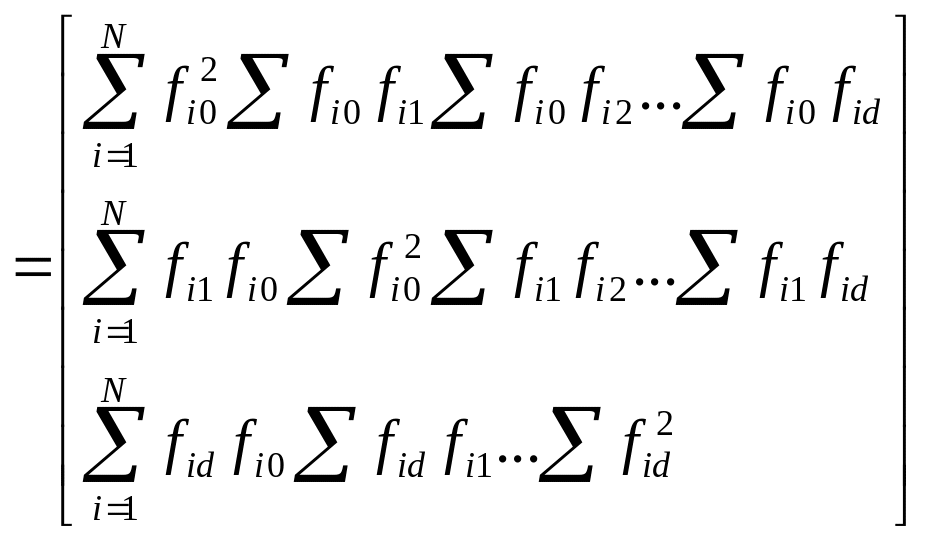

Вектор-столбец: Систему ур-ий для нахождения коэф-ов b принимает вид:

Ф