6Статический м-д исследования модели

М-д статических испытаний (Монте-Карло) представляет собой м-д получения с помощью ЭВМ статистических данных о процессах происходящих в моделируемой сис-ме.

Сущность м-да в построении моделируемого алгоритма для процессов функционирования исследуемой сис-мы, имитирующем поведение и взаимод-я элементов сис-мы с учетом случайных взаимодействий.

Выделяют 2 области применения м-да Монте-Карло:

1) Для моделирования объектов

2) численный м-од решения детерминированных задач.

Алгоритм применения м-да М.-К. для модел-я:

1.разработка детерминированной модели,описывающей функционирование объекта

2.Получение случайных чисел,соответствующих законам распределения стахостич. параметров объекта,влияние кот необходимо исследовать

3.расчёт значений вых параметров модели во всём диапазоне изменений детерминированныхпараметров для всех получившихся случ параметров

4.полученный набор значений рассматривается как реализация случайного процесса,т.е. знач-е вых параметров в кажд точке изменения детерминированных пар-ов рассматриваетси как выборка случайной величины и обрабатывается статистически(мат.ожидание,дисперсия,…)

7Способы получения случайных чисел.

1.аппаратный, случайное число вырабатываются с помощью случ.датчика.

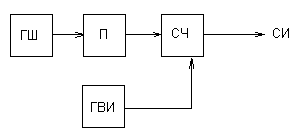
Достоинства: 1) Запас чисел неограничен: 2) не использ. ресурсы ЭВМ

Недостатки: 1) требуется периодическая проверка качества последовательности случайных чисел; 2) нельзя воспроизвести одинаковые последовательности; 3) необходимо специальное устройство.

2.табличный реализуется путем заполнения памяти ЭВМ некоторой проверенной последовательностью с.ч.

Д:1) не требуется проверка качества последовательности 2)м. воспроизводить одинак. последовательности.

Н:1) Запас чисел ограничен 2) нерациональное использовпание ресурсов ЭВМ

3.алгоритмический основан на формировании с.ч. в ЭВМ по некоторому алгоритму.

Д:1)Возможность воспроизведения одинак. последовательностей; 2)Однократная проверка кач-ва последовательности 3) малые затраты ресурсов ЭВМ

Н:1) Запас чисел ограничен

8Получение последовательностей с.Ч. С заданным з-ом распределения плотности вер-ти

1.Масштабирование

Если необходимо получить последовательность с.ч. с равномерным з-ком распределения в диапазоне [a;b], то , где - с.ч. из последовательности с равномерным з-ком распределения [0;1]. Если нужно получить с.ч. с нормальным з-ом распределения с заданными my, , то , где x-с.ч. с норм з-м распределения .ч. анными еления.ч. с нормальнымности вер-титерминированных пар-ов рассматриваетси как выборка случайной величины и обрабатыв

2.Преобразование закона распределения

Если с.в. имеет плотность распределения , то распределение с.в. ,где

Чтобы получить принадлежащее последовательности с распределением , необходимо решить интегральное уравнение:

, где - случайная величина с распределением [0;1]

Для пересчета в нормальный з-н распределения с параметрами , используется след-е ф-лы:

3.Приближенный универсальный способ получения с.ч. на основе кусочной аппроксимации ф-ии плотности В.

Алгоритм получения с.ч:

1) генерируется с.ч. равномерно распределенное в интервале [0;1]

2) по этому с.ч. выбирается номер интервала

3) генерируется с.ч. равномерно распределенное в интервале [0;1]

4) рассчитывается , где - с.ч. приближенно распределенное по требуемому з-ну.