3Этапы моделирования.Уровни мод-я.Требования к моделям
Этап 1.Уяснение и постановка задачи на физич.уровне, процесс схематизации явления и выделение его существенных особенностей.
Этап2.После выделения существенных факторов происходит перевод данных на язык мат-х понятий.Часто опираются на физич. з-ны принципы ТВ,…
Этап3. После построения модели следует проводить проверку логической непроворечивости и её адекватности явлению
Этап4.Все существенные данные из перечня параметров должны входить в матем-ю формулировку задачи.Справедливость модели проверяется по результатам решения теоретической задачи и сопоставления полученного результата с реальной ситуацией.
Уровни моделирования
1.Микроуровень (использует мат модели описывающие физическое состояние и процессы на сплошных средах). К типичным исследованием по параметрам относятся эл. потенциаллы, давление, плотность.
2.Макроуровень (в качестве объектов моделирования выделяют – отдельные функионально законченные элементы).
3.Метауровень (на этом уровне, путем дальнейшего абстрагирования физических процессов, полученные модели описывающие информационные процессы).
Требования к математическим моделям
1.Адекватность модели, т.е. отражаются заданные св-ва с заданной точностью.
2.Точность модели, определяется как степень совпадения значений выходных параметров модели и объекта. Чаще всего точность выражается погрешностью.
;
y-измеренное
значение вых.параметра;
-знач-е
вых.параметра,рассчит. по модели
3.Универсальность определяется числом и составом учитываемых в моделях внешних и выходных параметров.
4.Экономичность, характеризуется затратами вычислительных ресурсов для реализации модели
4Два подхода к моделированию
1) Классический: рассматривает объект моделирования путем перехода от частного к общему и синтезирует модель путем слияния ее компонентов
разрабатываемыми отдельно. взаимосвязано м/у отдельными частями модели рассматриваются как отражения связи м/у подсистемами объекта .
Реальный объект разрабатывается на отдельные подсистемы, т.е. выбираются исходные данные Д и ставятся цели Ц для нахождения этих подсистем. По отдельной совокупности исходных Д с учетом цели Ц, формируется компонент к будущей модели.Совокупность объединяется в модель(от частного к общему)
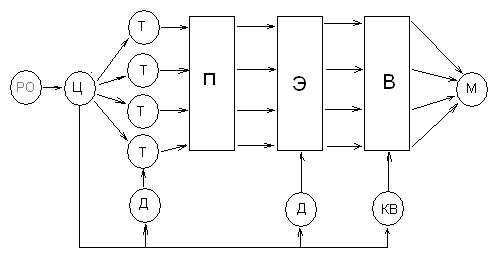
2) Системный: Предлагает последовательный переход от общего к частному. В основе моделирования лежит общая цель. На основе исходных данных и цели Ц формулируются требования Т к модели.На базе требований формируется подсистемы П и элементы Э будущей модели,кот на основе критерия выбора формируют состав модели М.
5Математические схемы описания моделирования.
Обьект моделирования описывается след. переменными:
-Входные
воздействия на систему
-Воздействия
внешней среды
-Внутренние
параметры системы
-Выходные
характеристики
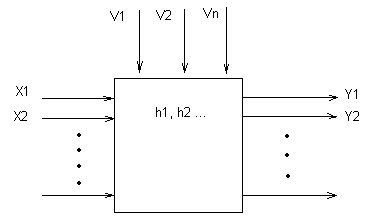
Процесс
функционирования объекта описывается
оператором
Совокупность
зависимостей вых. характеристик объекта
называется выходной
траекторией.
Схемы описания модели:
1.непрерывно-детерминированная схема – D – схемы, используется для описания модели систем функционирования непрерывно во времени,параметры кот м. принимать любое значение без учёта случ.возмущений этих параметров(диф.ур-я,сис-мы диф.ур-й ).
2.Дискретно-детерминированная схема - F-схемы, объект представляется в виде автомата(цифровой схемы),перерабатывающего дискретную информацию и изменяющего своё внутр.состояние в заданный момент времени.
3.Дискретно-стахастические схемы -P – схемы, объекты представляются дискретными преобразователями информации с памятью,функционирование кот определяется состоянием этой памяти и м.б. описана статистически
4.Непрерывно стохастические схемы Q - схемы, их объект мод-я представляется как сис-ма,исполняющая заявки на обслуживание.