3.2. Мода и медиана

Средние величины, описанные выше, являются обобщающими характеристиками совокупности по тому или иному признаку. Вспомогательными характеристиками являются, так называемые, структурные средние, к которым относятся мода, квартили, децили, медиана и др. Наиболее употребляемыми являются мода и медиана.

Мода  это величина, которая встречается в совокупности наиболее часто, то есть признак с наибольшей частотой. Этот показатель используется в тех случаях, когда требуется охарактеризовать наиболее часто встречающуюся величину признака (наиболее распространенный размер животноводческих ферм на сельскохозяйственных предприятиях, преобладающие цены на сельскохозяйственную продукцию и т. п. ).

Медианой называется величина, делящая численность упорядоченного вариационного ряда (расположенного в порядке возрастания или убывания признака) на две равные части. Медиана характеризует количественную границу значений изменяющегося признака, которыми обладает половина единиц совокупности. Например, если медианное значение удоя коровы составляет 4735 кг, то это означает, что половина коров имеет удой молока ниже 4735 кг и половина коров выше.

В дискретном вариационном ряду модой является признак с наибольшей частотой. Медианой является признак с номером, который находят путем деления суммы частот упорядоченного вариационного ряда на два и добавления 0,5.

В интервальном вариационном ряду моду находят по формуле:

,

где Мо  мода;

х_Мо  нижняя граница модального интервала;

h_Мо  величина модального интервала;

f_Мо  частота модального интервала;

f_Мо-1  частота интервала, предшествующего модальному;

f_Мо+1  частота интервала, следующего за модальным.

Модальным интервалом является интервал с наибольшей частотой.

Формула расчета медианы в интервальном вариационном ряду:

,

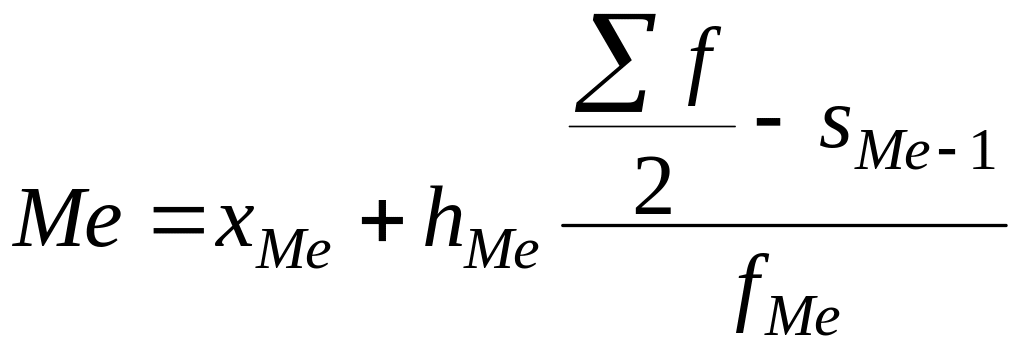где Ме  медиана;

х_Ме  нижняя граница медианного интервала;

h_Ме  величина медианного интервала;

 сумма частот;

s_Ме−1  сумма частот, накопленных в интервалах, предшествующих медианному;

f_Ме  частота медианного интервала.

Медианным интервалом является интервал, накопленная частота которого равна или превышает половину суммы частот.

Рассмотрим методику расчета моды и медианы.

Пример. Имеются данные о продуктивности норок (табл. 4).

Т а б л и ца 4

Приплод норок

Приплод на самку, гол.	Численность норок, гол.	Накопленные частоты
х	f	s
1 2 3 4 5 6 7	9 38 81 164 75 47 17	9 47 128 292 367 414 431
Итого		

Требуется определить моду и медиану.

Самую большую частоту  164 имеют норки с приплодом в 4 головы, следовательно, мода равна 4.

Медианой будет признак с номером . Из накопленных частот видно, что медианой будет норка, имеющая приплод в 4 головы.

Технология решения задачи в табличном процессоре Microsoft Excel следующая.

1. Введите исходные данные в соответствии с рис. 31.

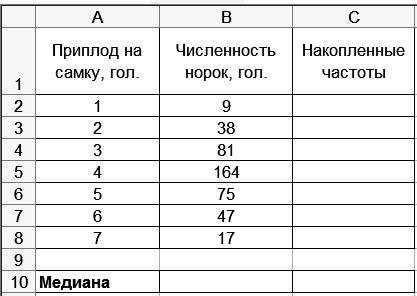
Р и с. 31

2. Рассчитайте накопленные частоты.

2.1. Скопируйте ячейку В2 в ячейку С2.

2.2. Введите в ячейку С3 формулу =С2+В3.

2.3. Скопируйте ячейку С3 в ячейки С4:С8.

3. Рассчитайте номер медианы. Для этого введите в ячейку С10 формулу =С8/2+0,5.

Результаты решения выводятся на экран дисплея в следующем виде (рис. 32).

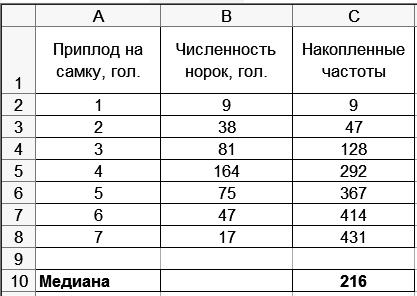
Р и с. 32

Пример. Имеются данные о среднесуточных приростах живой массы у молодняка крупного рогатого скота (табл. 5).

Т а б л и ц а 5

Среднесуточный прирост живой массы ремонтных телок

на откорме

Группы скота по среднесуточному приросту живой массы, г	Поголовье скота, гол.	Накопленные частоты
	f	s
500525 525550 550575 575600 600625 625650 650675 675700	21 36 98 143 136 100 86 10	21 57 155 298 434 534 620 630
Итого		

Требуется определить моду и медиану.

Моду и медиану рассчитывают по формулам для интервального вариационного ряда.

Для нахождения моды необходимо определить модальный интервал. Таким будет интервал 575600 с наибольшей частотой 143. Отсюда мода равна:

г.

Для нахождения медианы надо определить медианный интервал. Половина суммы частот равна 315 (630:2). Следовательно, согласно накопленным частотам медианным интер­валом будет 600  625 (315 < 434). Медиана равна: г.

Технология решения задачи в табличном процессоре Microsoft Excel следующая.

1. Введите исходные данные в соответствии с рис. 33.

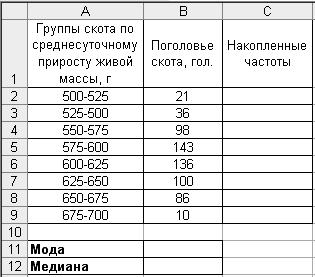
Р и с. 33

2. Рассчитайте накопленные частоты.

2.1. Скопируйте ячейку В2 в ячейку С2.

2.2. Введите в ячейку С3 формулу =С2+В3.

2.3. Скопируйте ячейку С3 в ячейки С4:С9.

3. Рассчитайте моду. Для этого введите в ячейку В11 формулу =575+25*(В5−В4)/(2*В5−В4−В6).

4. Рассчитайте моду. Для этого введите в ячейку В12 формулу =600+25*(С9/2−С5)/В5.

Результаты решения выводятся на экран дисплея в следующем виде (рис. 34).

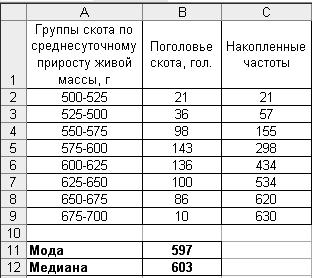
Р и с. 34