VI. Корреляционный анализ. Регрессия. Уравнение линии регрессии.

R (или r) – коэффициент корреляции. Устанавливает, есть ли связь между признаками, и насколько она тесная.

-1R1

Если же модуль коэффициента корреляции 1,то связь близка к линейной.

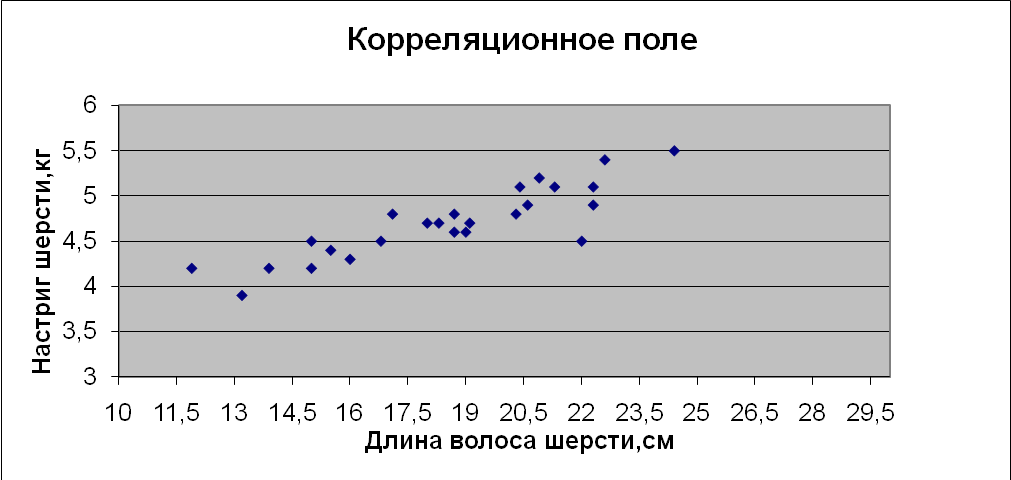
Рис. 9. Корреляционное поле.

Уравнение прямолинейной регрессии:

Таблица 9.

Регрессионная статистика
Множественный R	0,877540876
R-квадрат	0,770077989
Нормированный R-квадрат	0,76008138
Стандартная ошибка	0,193606006
Наблюдения	25

Таблица 10.

Дисперсионный анализ
	df	SS	MS	F	Значимость F
Регрессия	1	2,887484429	2,887484429	77,03391994	8,4375E-09
Остаток	23	0,862115571	0,037483286
Итого	24	3,7496

Таблица 11.

Параметры линии регрессии

	Коэффициенты	Стандартная ошибка	t-статистика	P-Значение
Y-пересечение	2,73573373	0,227573729	12,02130727	2,13329E-11
Длина волоса шерсти, см (x)	0,106209058	0,01210098	8,776896942	8,4375E-09

R=0,876

Вывод: связь между признаками тесная и близка к линейной.

R² (коэффициент детерминации) =0,77=77%

Вывод: вариация настрига шерсти обусловлена на 77% влиянием длины волоса шерсти. Остальные 23% вариации настрига обусловлены неучтенными факторами.

Для того, чтобы составить уравнение регрессии необходимо найти параметры B (У – пересечение) и .

Y-пересечение	2,7
Длина волоса шерсти, см (x)	0,106

Тогда уравнение регрессии будет иметь вид:

Вывод: При увеличении длины волоса шерсти на 1 см., настриг шерсти в среднем увеличивается на 106 г.