Решение с помощью функции линейн
ЛИНЕЙН
– это статистическая функция Microsoft
Excel,
позволяющая определять параметры
уравнения линейной регрессии
.
Технология решения задачи следующая.
1. Введите исходные данные в соответствии с рис. 63.
2. Рассчитайте параметры уравнения линейной регрессии .
2.1. Выделите ячейки В24:С28 (5 строк и 2 столбца).
2.2. Щелкните левой кнопкой мыши на панели инструментов на кнопке <Вставка функции> или выполните команду Вставка, fx Функция, щелкнув поочередно левой кнопкой мыши.
2.3. В диалоговом окне Мастер функций - шаг 1 из 2 с помощью левой кнопки мыши установите: Категория <Статистические>, Выберете функцию <ЛИНЕЙН> (рис. 73).
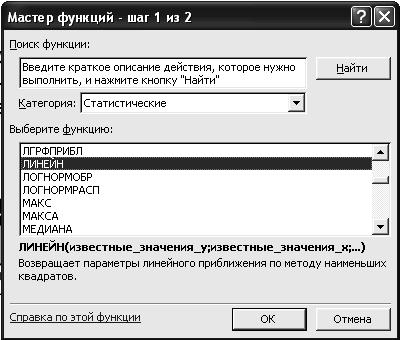
Р и с. 73
2.4. Щелкните левой кнопкой мыши на кнопке <ОК>.
2.5. На вкладке ЛИНЕЙН установите параметры в соответствии с рис. 74.
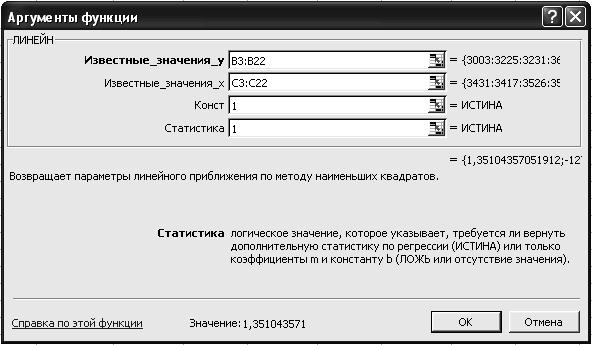
Р и с. 74
2.6. Щелкните левой кнопкой мыши на кнопке <ОК>.
2.7. Нажмите на клавишу <F2>, а затем на комбинацию клавиш <Ctrl>+<Shift>+<Enter>.
Результаты решения выводятся на экран дисплея в следующем виде (рис. 75).
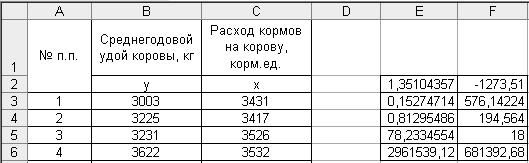
Р и с. 75
В табл. 15 приведено название показателей, значение которых дано в ячейках Е2:F6 на рис. 75.
Т а б л и ц а 15
Название показателей, выводимых с помощью функции линейн
Столбец Строка |
Е |
F |
2 |
Значение коэффициента а1 |
Значение коэффициента а0 |
3 |
Среднеквадратическое отклонение а1 |
Среднеквадратическое отклонение а0 |
4 |
Коэффициент детерминации r2 |
Среднеквадратическое отклонение у |
5 |
F-критерий |
Число степеней свободы вариации |
6 |
Регрессионная сумма квадратов |
Остаточная сумма квадратов |
В
Microsoft
Excel
также используется статистическая
функция ЛГРФПРИБЛ
для вычисления параметров уравнения
экспоненциальной регрессии
.
Технология решения аналогична применению
функции ЛИНЕЙН.
Решение с помощью надстройки Анализ данных
Анализ данных – это надстройка Microsoft Excel, предназначенная для статистических расчетов. Технология решения следующая.
1. Введите исходные данные в соответствии с рис. 63.
2. Рассчитайте параметры уравнения линейной регрессии .
2.1. Выполните команду Сервис, Анализ данных, щелкнув поочередно левой кнопкой мыши.
2.2. В диалоговом окне Анализ данных с помощью левой кнопки мыши установите: Инструменты анализа <Регрессия> (рис. 76).
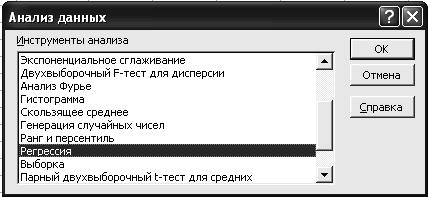
Р и с. 76
2.3. Щелкните левой кнопкой мыши на кнопке <ОК>.
2.4. На вкладке Регрессия установите параметры в соответствии с рис. 77.
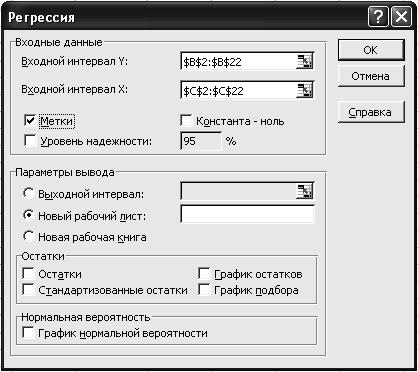
Р и с. 77
2.5. Щелкните левой кнопкой мыши на кнопке <ОК>.
Результаты решения выводятся на экран дисплея в следующем виде (рис. 78).
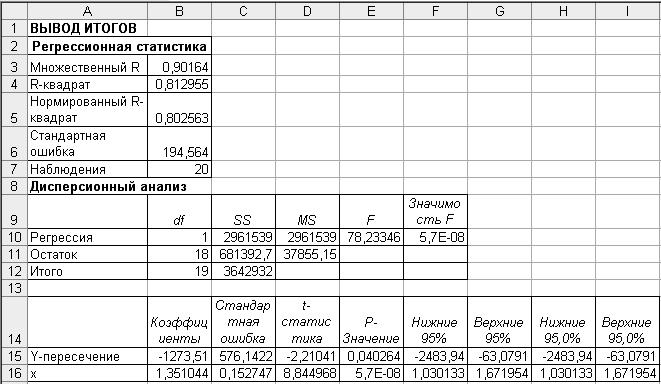
Р и с. 78
Пояснения к названию отдельных показателей на рис. 78 приведены в табл. 16.
Т а б л и ц а 16
Название показателей, выводимых с помощью надстройки Анализ данных
Наименование в Microsoft Excel |
Принятые наименования |
Множественный R |
Коэффициент (индекс) множественной корреляции (в рассмотренном примере парной корреляции) |
R-квадрат |
Коэффициент (индекс) детерминации |
df |
Число степеней свободы вариации |
SS |
Сумма квадратов |
MS |
Дисперсия |
F |
F-критерий |
t-статистика |
t-критерий |