5. Показатели распределения

Коэффициент асимметрии для выборки рассчитывается по формуле:

где A_s – коэффициент асимметрии;

– момент третьего порядка;

– выборочное среднее квадратическое отклонение;

n – число вариант.

Показатель эксцесса для выборки рассчитывается по формуле:

или ,

где – эксцесс;

– момент четвертого порядка.

Пример. Имеются выборочные данные о сервис-периоде по 25 коровам (табл. 7).

Т а б л и ц 7

Сервис-период коров

№ п/п	Сервис-период, дн.	Квадрат сервис-периода	Нормированное отклонение от средней
			в третьей степени	в четвертой степени
	х	х2
1	77	5929	-1,4272	1,6069
2	86	7396	-0,0302	0,0094
3	99	9801	0,6477	0,5605
4	68	4624	-7,3064	14,1777
5	83	6889	-0,1980	0,1154
6	83	6889	-0,1980	0,1154
7	98	9604	0,4650	0,3602
8	83	6889	-0,1980	0,1154
9	89	7921	-0,0001	0,0000
10	82	6724	-0,3053	0,2056
11	77	5929	-1,4272	1,6069
12	91	8281	0,0028	0,0004
13	83	6889	-0,1980	0,1154
14	85	7225	-0,0649	0,0261
15	92	8464	0,0124	0,0029
16	106	11236	3,3668	5,0460
17	106	11236	3,3668	5,0460
18	88	7744	-0,0022	0,0003
19	83	6889	-0,1980	0,1154
20	109	11881	5,5480	9,8216
21	86	7396	-0,0302	0,0094
22	107	11449	4,0143	6,3798
23	80	6400	-0,6237	0,5328
24	87	7569	-0,0108	0,0024
25	108	11664	4,7399	7,9620
Итого

Требуется рассчитать основные статистические показатели распределения, характеризующие данную выборочную совокупность.

Средняя продолжительность сервис-периода коров:

дн.

Выборочная дисперсия сервис-периода коров:

.

Выборочное среднее квадратическое отклонение сервис-периода коров:

дн.

Асимметрия сервис-периода коров:

.

Эксцесс сервис-периода коров:

.

Полученные значения асимметрии и эксцесса показывают, что данное распределение имеет правостороннюю асимметрию и более высокую вариацию, чем при нормальном распределении.

Технология решения задачи в табличном процессоре Microsoft Excel следующая.

1. Введите исходные данные в соответствии с рис. 39.

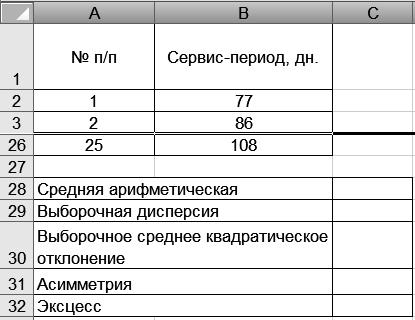
Р и с39

2. Рассчитайте средний сервис-период коров.

2.1. Выделите ячейку С28.

2.2. Щелкните левой кнопкой мыши на панели инструментов на кнопке <Вставка функции> или выполните команду Вставка, f_x Функция, щелкнув поочередно левой кнопкой мыши.

2.3. В диалоговом окне Мастер функций - шаг 1 из 2 с помощью левой кнопки мыши установите: Категория  <Статистические>, Выберете функцию  <СРЗНАЧ> (рис. 40).

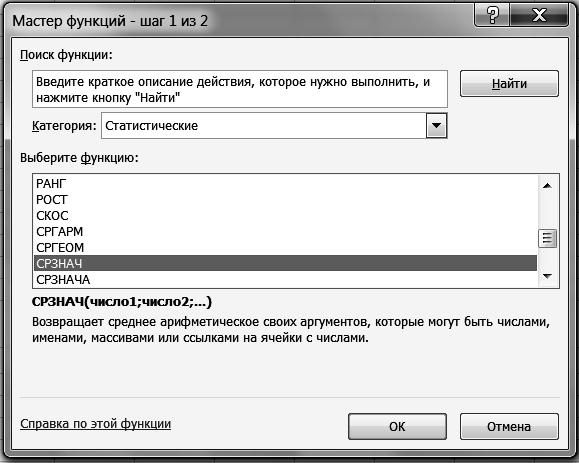
Р и с. 40

2.4. Щелкните левой кнопкой мыши на кнопке <ОК>.

2.5. На вкладке СРЗНАЧ установите параметры в соответствии с рис. 41.

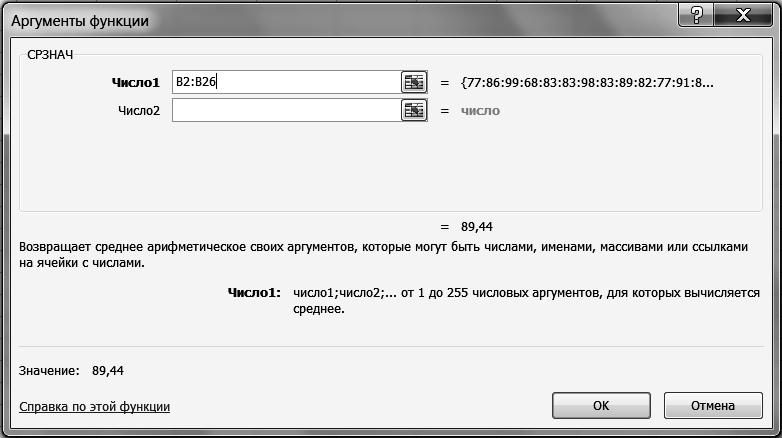
Р и с. 41

2.6. Щелкните левой кнопкой мыши на кнопке <ОК>.

3. Рассчитайте выборочную дисперсию. Для этого используйте статистическую функцию ДИСПА.

4. Рассчитайте выборочное среднее квадратическое отклонение. Для этого используйте статистическую функцию СТАНДОКЛОНА.

5. Рассчитайте асимметрию. Для этого используйте статистическую функцию СКОС.

6. Рассчитайте эксцесс. Для этого используйте статистическую функцию ЭКСЦЕСС.

Результаты решения выводятся на экран дисплея в следующем виде (рис. 42).

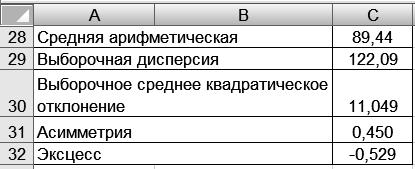
Р и с. 42