Выводы:

• Никаких ограничений на число «1» и число «0» в описанной процедуре не накладывается, поэтому подход можно применить для любой функции, с любым числом переменных;

• При составлении формул мы использовали символы логических операций НЕ, И, ИЛИ, и, следовательно, с помощью этих операций можно составить формулу для любой логической функции;

• Совокупность логических операций, позволяющая составить формулу для любой логической функции, называется функционально полной системой операций (функций) или базисом.

Примечание: Операцией называется функция, значения аргументов которой и ее собственные значения принадлежат одному множеству. Когда речь идет о функционально полных системах логических операций, то чаще употребляют выражение «функционально полная система функций».

На основе полученных результатов можно сформулировать такие правила составления СДНФ.

Правила составления сднф

1. В таблице истинности найти строки, имеющие в графе функции значения «1».

2. Записать выражение в виде логической суммы произведений переменных. Количество произведений равно числу единиц в графе функции.

3. В каждом произведении над входными переменными, имеющими значение «0» в соответствующей строке таблицы истинности, поставить символ отрицания.

2.3.2. Совершенная конъюнктивная нормальная форма

При построении СДНФ мы использовали единичные наборы таблицы истинности (наборы, на которых функция имеет значение 1). Если провести подобные рассуждения, используя нулевые наборы (наборы, на которых функция равна 0), то получим другую совершенную нормальную форму функции. Для получения такой формы функции нашего примера мы не будем проводить логические исследования, а используем правила построения СДНФ.

Итак, СДНФ строится по единичным наборам. А что нужно сделать, чтобы нули в графе функции превратить в единицы? Очевидно, надо исследовать не функцию y, а инверсную ей , приведенную в табл. 13.

Таблица 13
№	c	b	а	y
0	0	0	0	0	1
1	0	0	1	0	1
2	0	1	0	0	1
3	0	1	1	1	0
4	1	0	0	0	1
5	1	0	1	1	0
6	1	1	0	1	0
7	1	1	1	1	0

Табл. 13 получена из табл. 12 добавлением графы , в которой помещены значения, инверсные по отношению к значениям функции y (инверсные значения получаются заменой 0 на 1 и 1 на 0).

По правилам, изложенным выше, составим совершенную дизъюнктивную нормальную форму для инверсной функции

= = 1.

Возьмем отрицание от полученной формулы и преобразуем ее, используя законы булевой алгебры:

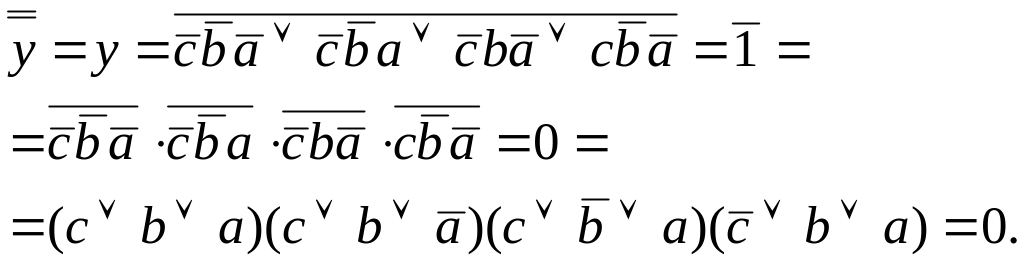
Замечание: 0 обычно не пишется, но всегда подразумевается.

Получили совершенную конъюнктивную нормальную форму (СКНФ) функции y в виде произведения (конъюнкции) логических сумм (дизъюнкций) всех аргументов или их отрицаний. СКНФ всякой логической функции также, как и СДНФ, единственна.

Дизъюнкции, входящие в СКНФ, называются макстермами или конституентами нуля. Понятия «макстерм» и «конституента нуля» будут пояснены ниже.

Полученная форма называется

• совершенной, так как все дизъюнкции содержат все переменные (с отрицанием или без отрицания);

• конъюнктивной, потому что формула представляет собой конъюнкцию дизъюнкций;

• нормальной, так как все дизъюнкции являются элементарными.

Если в дизъюнкцию входят только переменные или их отрицания, то она называется элементарной. Число переменных в дизъюнкции называется ее рангом. В нашем случае ранг дизъюнкций равен 3.

Проведем анализ формулы, представляющей СКНФ.

Функция y равна 0, если хотя бы одна дизъюнкция (выражение в паре скобок) равна 0.

Первая дизъюнкция будет равна 0 только тогда, когда a = 0, b = 0, c = 0, что соответствует нулевому набору переменных . (вспомним, если a = 0, то пишем ). Равенство нулю проверяется подстановкой соответствующих значений переменных.

Вторая дизъюнкция будет равна 0 только тогда, когда a = 1, b = 0, c = 0, что соответствует первому набору .

Третья дизъюнкция будет равна 0 только тогда, когда a = 0, b = 1, c = 0, что соответствует второму набору .

Четвертая дизъюнкция будет равна 0 только тогда, когда a = 0, b = 0, c = 1, что соответствует четвертому набору .

Таким образом, каждая дизъюнкция соответствует своему набору переменных, на котором функция y равна 0.

На основе полученных результатов можно сформулировать такие правила составления СКНФ.