1.4.2. Инверсные функции
У каждой логической функции есть инверсная функция.
Инверсная функция – это функция, значения которой на каждом входном наборе инверсны значениям прямой функции.
Если функция задана таблицей истинности, то ее инверсная функция получается заменой в графе функции 0 на 1, а 1 на 0. Произведя аналогичные действия над значениями инверсной функции, можно получить прямую функцию. Какую функцию считать прямой, а какую инверсной – это определяет разработчик.
Инверсная
функция для
(табл. 5) обозначается как
,
а ее таблица истинности приведена в
табл. 8. Это функция
– эквивалентность.
По
определению Теории множеств (да и по
обозначению) инверсная функция булевой
алгебры это не что иное, как дополнение
прямой функции до единицы. Действительно,
для
получаем
1.5. Приоритеты операций
Логические операции выполняются в следующем порядке:
– инверсия (НЕ) отдельных переменных имеет самый высокий приоритет;
– конъюнкция (И) имеет приоритет второго уровня;
– дизъюнкция (ИЛИ) имеет приоритет третьего уровня;
Операции →,←,, не имеют приоритета и выполняются по очереди слева направо.
Операции | и ↓ являются групповыми инверсиями и их следует понимать как скобки.
Для того чтобы не ошибиться с порядком выполнения операций применяют скобки. Если в формуле имеется несколько пар скобок, то операции в скобках выполняются в каждой паре скобок в соответствии с приоритетами, а пары скобок рассматриваются последовательно, например, слева направо.
Пример:
1
2 5 3 4 6 
порядок выполнения операций
[(
d)
(
c)]→e.
1.6. Законы и тождества булевой алгебры
Законы нуля: a 0 = a; a 0 = 0; 0 a b c ….= 0.
Законы единицы: a 1 = a; a 1 = 1; 1 a b c ….=1.
Законы повторения: a а = a; aа = a;
a а а а …= a; aааа…= a.
Закон двойного отрицания:
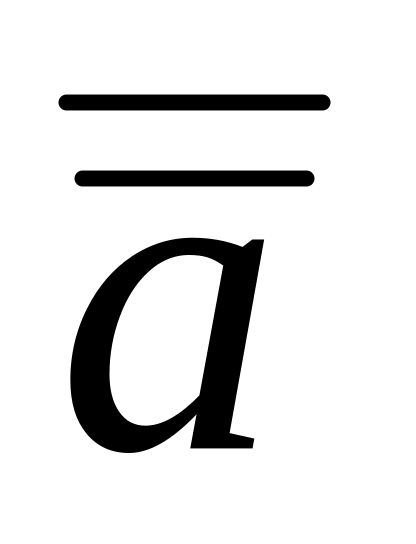= a.Законы дополнительности: а = 0; a
=
1.Коммутативные законы: ab = ba; a b = b a.
Ассоциативные законы: a (bc) = (ab)c = abc;
a (b c) = (a b) c = a b c.
Дистрибутивные законы:
а) конъюнкции относительно дизъюнкции:
a (b c) = ab ac; ad(b c) = abd acd;
б) дизъюнкции относительно конъюнкции:
a bc = (a b)(a c); a bc d = (a b d)(a c d);
доказательство: рассмотрим правую часть первой формулы
(a b)(a c)= aa ac ba bc,
так как aa = a, то a ac = a(1 c) = a и a ab = a(1 b) = a.
Следовательно, (a b)(a c) = aa ac ba bc = a bc.
Законы поглощения:
a(a b) = a, доказательство: a(a b) = aa ab = a(1 b) = a1 = a.
a(a b)(a c)…= a; (a b)(a b c) = a b; ab abc = ab.
a( b) = ab; доказательство: a( b) = a ab = 0 ab = ab.
Законы склеивания:
ab
a
=
a,
доказательство:
ab
a
=
a(b
)
= a1 = a;
(a
b)(a
)
= a, доказательство:
(a
b)(a
)
= a
= a – см. доказательство
дистрибутивного закона 8,б.
Законы обобщенного склеивания: (доказательства см. п.4.1.3)
Законы де Моргана:
;
;
;
.
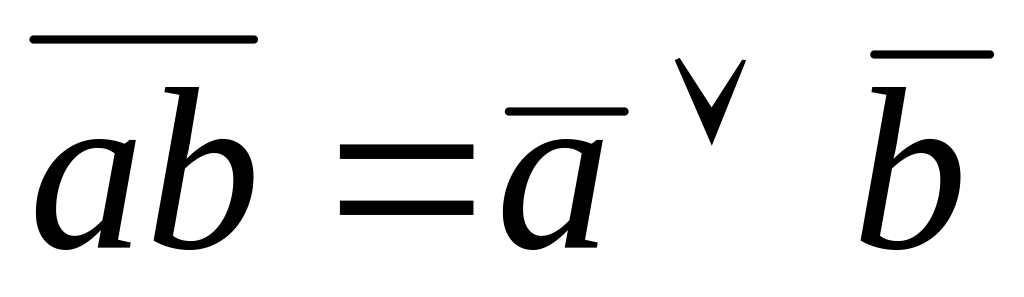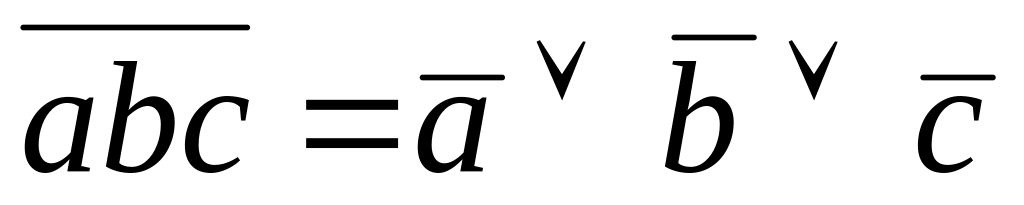Разложение функций по переменным:
f(a,b,c,…,w) = af(1,b,c,…,w) f(0,b,c,…,w); (1)
f(a,b,c…w) = [a f(0,b,c,…,w)] [ f(1,b,c,…,w)]; (2)
af(a,b,c,…,w) = af(1,b,c,…,w);
a f(a,b,c,…,w) = a f(0,b,c,…,w);
f(a,b,c,…,w) = f(0,b,c,…,w);
f(a,b,c,…,w) = f(1,b,c,…,w).
Законы справедливы и если вместо переменных подставить правильные логические выражения (формулы).
Доказательство наиболее простых законов производится с помощью аксиом, а других с использованием уже доказанных законов.
Доказательство формул типа (1) и (2) производят с помощью подстановок а = 1, = 0, затем а = 0, = 1.
В общем случае для доказательства законов и тождеств в булевой алгебре применяют два подхода:
– первый – с помощью таблиц истинности, которые составляются для левой и правой частей предполагаемого тождества и сравниваются;
– второй – с применением преобразований логических выражений в левой и правой части предполагаемого тождества с помощью уже доказанных законов и тождеств и последующим сравнением результатов.
(Примеры преобразований см. Раздел 7.)