С помощью эквивалентных преобразований привести формулу к днф, кнф, сднф, скнф, получить полином Жегалкина.
Дана формула 
.
Решение:
Преобразуем:
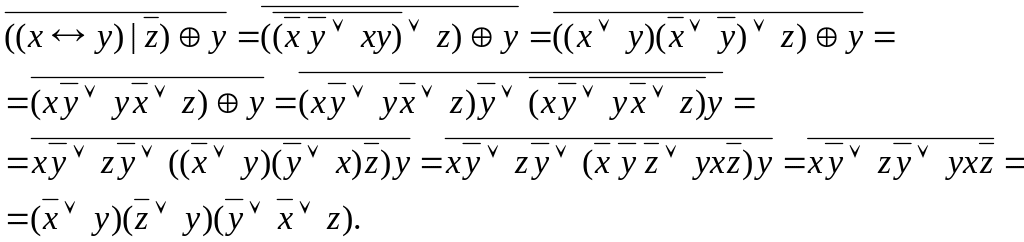
Получили КНФ.
Раскрыв скобки, и приведя подобные члены, получим ДНФ:
Вместо недостающих переменных в термы ДНФ ставим 1, выполнив преобразования, получим СДНФ:
в термы КНФ вместо недостающих переменных ставим 0, выполнив преобразования, получим СКНФ:
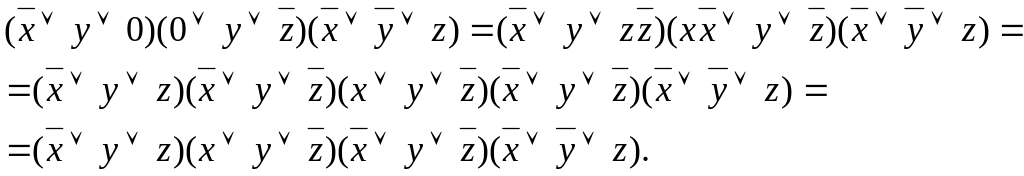
Полином Жегалкина построим преобразованием ДНФ:
Результаты преобразований:
– КНФ,
– ДНФ,
–
СДНФ,
– СКНФ,
– Полином Жегалкина.
С помощью карт Карно найти все минимальные днф функции трех переменных ƒ(X,y,z).
Дано:
.
Решение:
Функция задана нулевыми наборами {0, 1, 4, 6}, значит, на остальных наборах она имеет значения, равные 1.
Строим таблицу истинности:
Таблица 39 |
||||
№ |
x |
y |
z |
ƒ |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
2 |
0 |
1 |
0 |
1 |
3 |
0 |
1 |
1 |
1 |
4 |
1 |
0 |
0 |
0 |
5 |
1 |
0 |
1 |
1 |
6 |
1 |
1 |
0 |
0 |
7 |
1 |
1 |
1 |
1 |
Составляем карту Карно и определяем минимальную ДНФ функции:
Таблица 40 |
||||
xy/ z |
00 |
01 |
11 |
10 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
– минимальная ДНФ функции.
Других вариантов нет.
С помощью карт Карно найти все минимальные днф и кнф булевой функции четырех переменных , заданной вектором своих значений.
Дано: = (1110 1001 0111 0001),
где первый символ слева – значение функции при входном наборе 0000.
Решение:
Строим таблицу истинности:
Таблица 41 |
|||||
№ |
x1 |
x2 |
x3 |
x4 |
ƒ |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
2 |
0 |
0 |
1 |
0 |
1 |
3 |
0 |
0 |
1 |
1 |
0 |
4 |
0 |
1 |
0 |
0 |
1 |
5 |
0 |
1 |
0 |
1 |
0 |
6 |
0 |
1 |
1 |
0 |
0 |
7 |
0 |
1 |
1 |
1 |
1 |
8 |
1 |
0 |
0 |
0 |
0 |
9 |
1 |
0 |
0 |
1 |
1 |
10 |
1 |
0 |
1 |
0 |
1 |
11 |
1 |
0 |
1 |
1 |
1 |
12 |
1 |
1 |
0 |
0 |
0 |
13 |
1 |
1 |
0 |
1 |
0 |
14 |
1 |
1 |
1 |
0 |
0 |
15 |
1 |
1 |
1 |
1 |
1 |
Составляем карты Карно и определяем минимальные ДНФ функции:
Таблица 42 |
||||
x1x2/ x3x4 |
00 |
01 |
11 |
10 |
00 |
1 |
1 |
0 |
0 |
01 |
1 |
0 |
0 |
1 |
11 |
0 |
1 |
1 |
1 |
10 |
1 |
0 |
0 |
1 |
– минимальная ДНФ функции.
Здесь возможен и другой вариант (см. табл. 43)
Таблица 43 |
||||
x1x2/ x3x4 |
00 |
01 |
11 |
10 |
00 |
1 |
1 |
0 |
0 |
01 |
1 |
0 |
0 |
1 |
11 |
0 |
1 |
1 |
1 |
10 |
1 |
0 |
0 |
1 |
По таблице 44 получаем минимальную КНФ функции
.
Других вариантов нет.
Таблица 44 |
||||
x1x2/ x3x4 |
00 |
01 |
11 |
10 |
00 |
1 |
1 |
0 |
0 |
01 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
10 |
1 |
0 |
0 |
1 |
1