
- •Содержание
- •Введение
- •1. Функции алгебры логики и их свойства
- •1.1. Функции одной переменной
- •1.2. Функции двух переменных
- •1.4. Обратные и инверсные логические функции
- •1.4.1. Обратные функции
- •Прямое соответствие (рис. 2,а)
- •Обратное соответствие (рис. 2,б)
- •1.4.2. Инверсные функции
- •1.5. Приоритеты операций
- •1.6. Законы и тождества булевой алгебры
- •1.7. Вопросы для самоконтроля
- •2. Формы задания логических функций
- •2.1. Словесная форма
- •2.2. Табличная форма
- •2.3. Задание формулой
- •2.3.1. Совершенная дизъюнктивная нормальная форма
- •Выводы:
- •Правила составления сднф
- •2.3.2. Совершенная конъюнктивная нормальная форма
- •Правила составления скнф
- •2.3.3. Дизъюнктивные и конъюнктивные нормальные формы
- •2.3.4. Минтермы, макстермы и их свойства
- •2.4. Другие формы задания логических функций
- •2.5. Вопросы для самоконтроля
- •3. Функционально полные системы функций
- •Штрих Шеффера
- •Стрелка Пирса
- •Импликация и «0»
- •3.1. Теорема Поста–Яблонского
- •3.1.1. Определение минимального базиса
- •3.1.2. Функции, не сохраняющие 0 и 1
- •3.1.3. Двойственная функция
- •3.1.4. Монотонная функция
- •3.3. Вопросы для самоконтроля
- •4. Минимизация логических функций
- •4.1. Расчетный метод
- •4.1.1. Склеивание
- •4.1.2. Поглощение
- •4.1.3. Развертывание
- •4.2. Карты Карно
- •4.3. Минимизация систем логических уравнений
- •4.4. Частично определенная логическая функция
- •4.5. Вопросы для самоконтроля
- •5. Синтез и анализ логических схем
- •5.1. Схемы на переключателях, диодах и транзисторах
- •5.2. Схемы на логических элементах
- •5.2.1. Реализация функции на элементах и, или, не
- •5.2.2. Реализация функции на элементах и–не
- •5.2.3. Реализация функции на элементах или–не
- •5.3. Анализ схем
- •5.4. Оценка качества схем
- •5.5. Вопросы для самоконтроля
- •6. Булева производная
- •6.1. Контроль работоспособности логических схем
- •6.2. Построение тестов методом булевой производной
- •6.2.1. Свойства булевой производной
- •6.3. Вопросы для самоконтроля
- •7. Примеры преобразований логических функций
- •7.1. Представление логических функций в системе и, или, не
- •7.2. Построение таблиц истинности
- •7.3. Преобразование кнф в днф и днф в кнф Преобразование кнф в днф
- •Преобразование днф в кнф
- •7.4. Доказательства равенства логических функций
- •7.5. Разложение логических функций по переменным
- •7.5.1. Последовательное разложение по всем переменным Разложение по п. 1.6.13 (1)
- •Разложение по п. 1.6.13 (2)
- •7.5.2. Параллельное разложение по всем переменным разложение по п. 1.6.13 (1)
- •Разложение по п. 1.6.13 (2)
- •8. Домашняя работа
- •8.1. Задание
- •8.2. Выполнение
- •Проверить двумя способами эквивалентность формул
- •С помощью эквивалентных преобразований привести формулу к днф, кнф, сднф, скнф, получить полином Жегалкина.
- •С помощью карт Карно найти все минимальные днф функции трех переменных ƒ(X,y,z).
- •С помощью карт Карно найти все минимальные днф и кнф булевой функции четырех переменных , заданной вектором своих значений.
- •Является ли полной система функций? Образует ли она минимальный базис?
- •9. Список литературы
- •Введение в булеву алгебру
- •Гоу впо “Московский государственный университет приборостроения и информатики”
- •107996, Москва, ул. Стромынка, 20
6.2. Построение тестов методом булевой производной
Предположим, что схема рис. 19 описывается функцией
f(x) = f(x1, x2,…, xj,…, xn) .
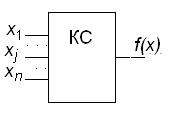
Рисунок 19 – Условное обозначение схемы
для пояснения понятия «булевой производной»
Пусть на входе xj возникла неисправность “константа 0” ( 0).
Чтобы обнаружить ее, необходимо сделать xj существенной переменной, т.е. чтобы при изменении xj менялось значение выхода f(x). Это условие можно записать так
f(x1,x2,…,![]() ,…,xn)
f(x1,x2,…,
,…,xn)
f(x1,x2,…,![]() ,…,xn)
= 1 .
,…,xn)
= 1 .
(Обратите внимание на и .)
Или коротко
f( ) f( ) = 1 .
Это выражение равно 1 тогда и только тогда, когда только одно из значений f( ) или f( ) равно 1. Если же оба значения одинаковы, т.е. f(x) не управляется , то сумма по модулю два равна 0.
Сумма f( ) f( ) носит название булевой производной или булевой разности и обозначается
![]() f(
)
f(
)
.
f(
)
f(
)
.
Решение уравнения
1
определяет набор переменных (не ), который позволяет обнаружить неисправность на входе . Значения же определяются из условий:
для обнаружения неисправности 0 надо подать на вход 1,
для обнаружения неисправности 1 надо подать на вход 0.
Таким образом, для определения набора входных переменных, обнаруживающего неисправность 0, надо решить уравнение
![]() 1, (1)
1, (1)
а для неисправности 1 соответственно уравнение
1. (2)
Производные удобнее определять по выражению
f(x1, x2,…, 1,…, xn) f(x1, x2,…, 0,…, xn)
или проще
f(1) f(0),
где заменена на 1, а на 0.
В логическом базисе И, ИЛИ, НЕ булева производная запишется так
![]() .
(3)
.
(3)
В общем случае переменная не обязательно входная – это может быть внутренняя (промежуточная) или даже выходная переменная.
6.2.1. Свойства булевой производной
При решении уравнений (1) и (2) широко используются свойства булевой производной:
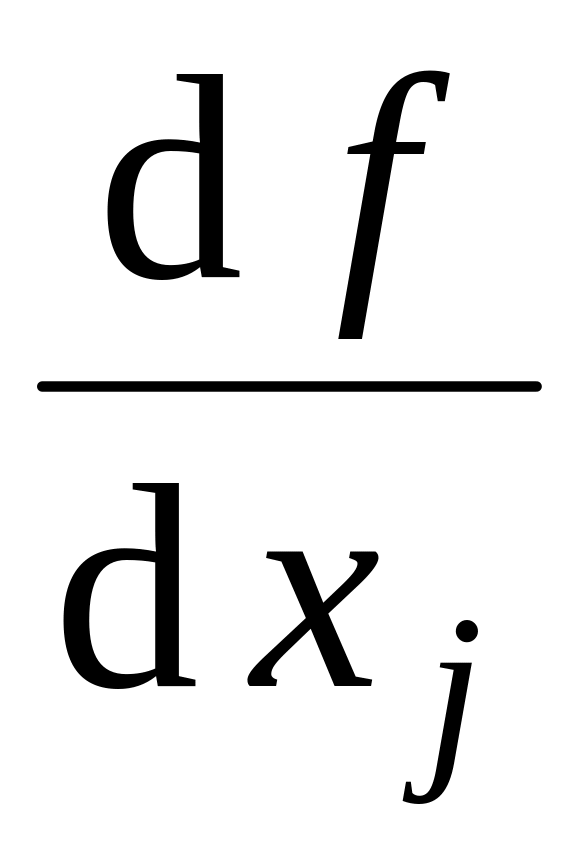 – не зависит от
.
– не зависит от
.Решение уравнения g(x) = 1 определяет набор
 ,
при котором
становится существенной переменной.
,
при котором
становится существенной переменной.Решение уравнения g(x) = 0 определяет набор , при котором не влияет на выходную функцию f(x).
Если
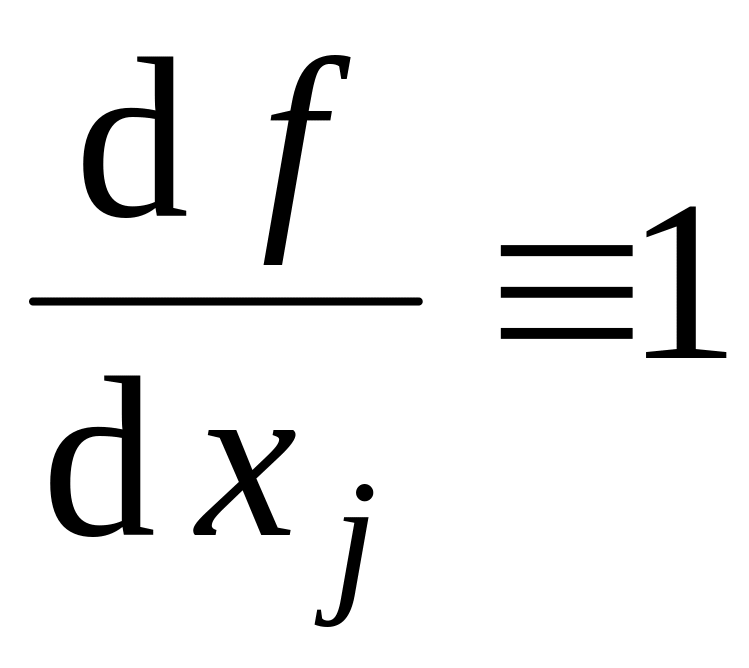 ,
то
,
то
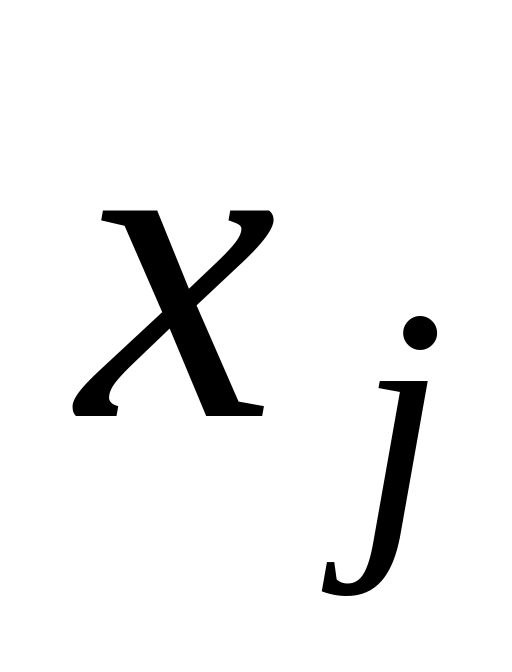 всегда является существенной.
всегда является существенной.Если
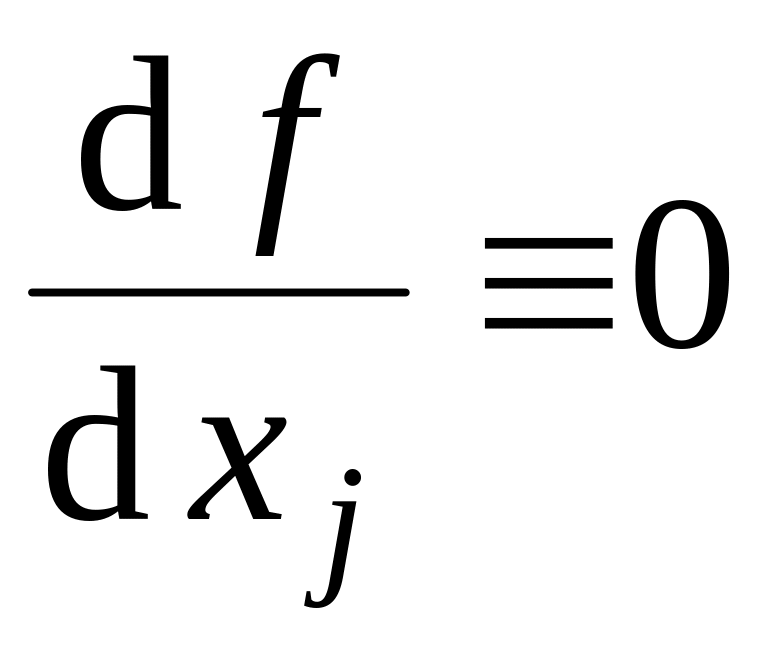 ,
то f не зависит от
.
,
то f не зависит от
.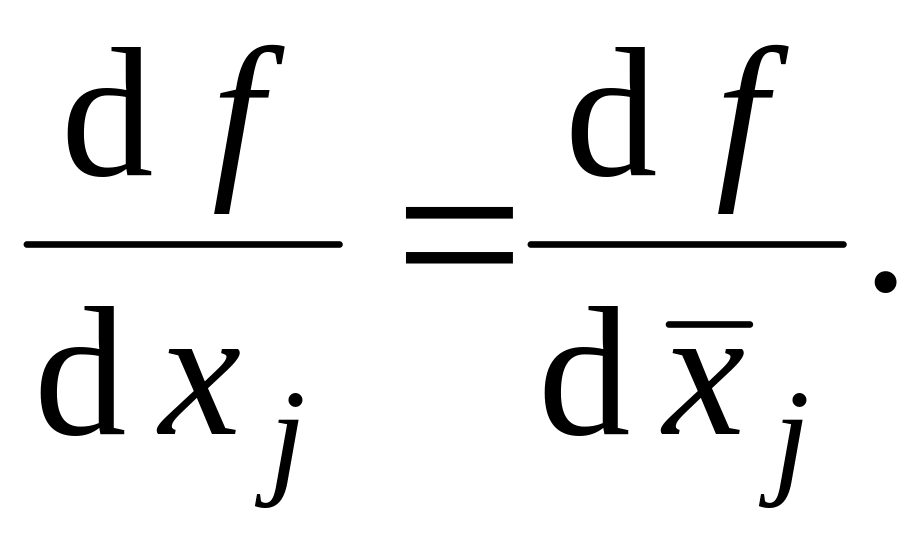
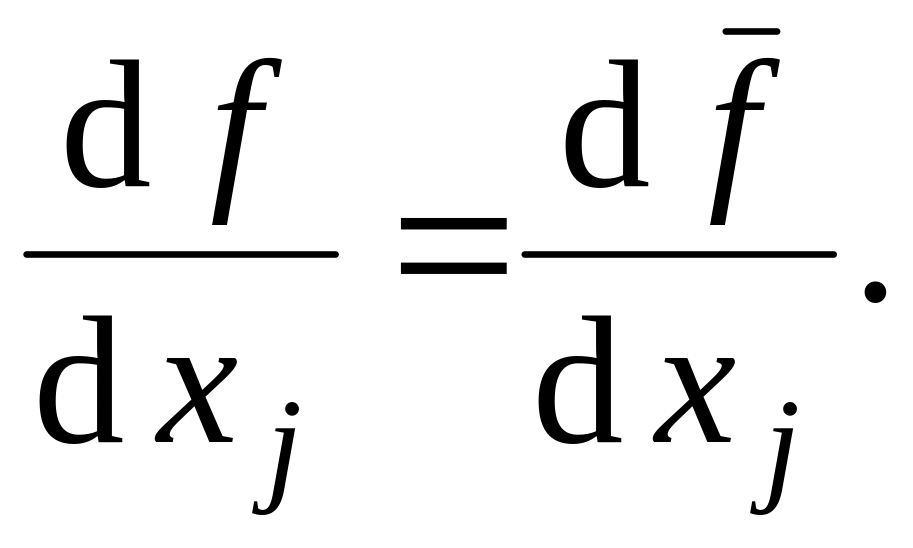
Свойства 6 и 7 следуют из симметричности формулы (3) относительно и f.
Следствие: если f1 не зависит
от xj , то
![]()
Следствие: если f1 не зависит
от xj , то
![]()
10. ![]()
Следствие: если f1 не зависит
от xj, то
![]()
где k – промежуточная точка схемы такая, что пути от j к выходу идут через k.
Булевы производные функций, реализуемых типовыми элементами:
Для f = x1x2…xj…xn и f =
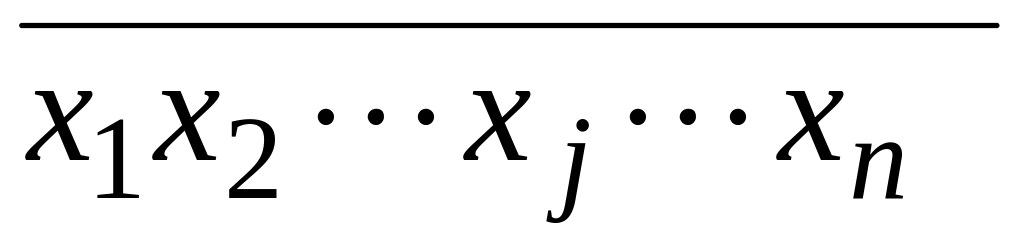
![]()
Для f =
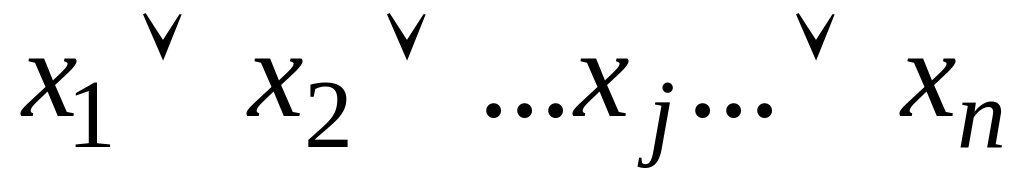 и f =
и f =
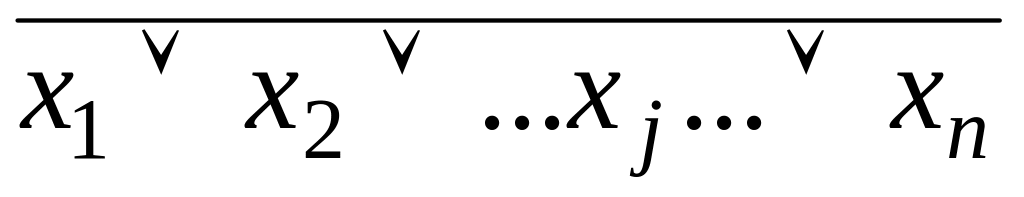
![]()
Для f = x и f =
![]()
Для
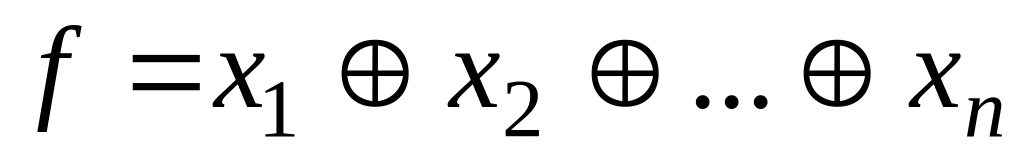
![]() , j
=
, j
=
![]() .
.
Пример 1:
Найти наборы для обнаружения неисправностей на входе a схемы рис. 20.
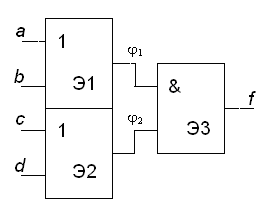
Рисунок 20 – Схема к примеру 1
Для определения тестового набора неисправности а 0 надо решить уравнение
![]() (4)
(4)
Решаем, используя свойства булевой производной:
![]() ,
,
![]() (свойство 11),
(свойство 11),
![]()
Или
сразу
![]() (следствие свойства 8).
(следствие свойства 8).
![]()
Или
сразу
![]() (по выражению 12,b).
(по выражению 12,b).
Следовательно,
![]() (5)
(5)
Для уравнения (4) получаем
![]()
или
![]()
В обоих произведениях отсутствует по одной переменной, поэтому для каждого из них будет по два решения – по два набора.
![]()
![]()
Следовательно, наборы для обнаружения неисправности а 0 будут такими
1) |
a |
b |
c |
d |
|
2) |
a |
b |
c |
d |
|
1 |
0 |
1 |
1 |
|
|
1 |
0 |
1 |
1 |
|
1 |
0 |
1 |
0 |
|
|
1 |
0 |
0 |
1 |
Объединяя 1) и 2), получаем
a |
b |
c |
d |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
Любой из этих наборов обнаруживает неисправность а 0.
Для неисправности а 1 надо решить уравнение
![]() .
.
Производную
![]() мы уже знаем (5), она равна
мы уже знаем (5), она равна
![]() ,
поэтому получаем
,
поэтому получаем
![]() .
.
Следовательно, имеем два решения
![]()
В обоих произведениях отсутствует по одной переменной, поэтому для каждого из них будет по два решения – по два набора.
![]()
![]()
Или
1) |
a |
b |
c |
d |
|
2) |
a |
b |
c |
d |
|
0 |
0 |
1 |
1 |
|
|
0 |
0 |
1 |
1 |
|
0 |
0 |
1 |
0 |
|
|
0 |
0 |
0 |
1 |
Объединяя, получаем
a |
b |
c |
d |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
Любой из этих наборов обнаруживает неисправность а 1.
Пример 2:
Найти наборы для обнаружения неисправностей на входах и выходах сумматора (рис. 21).
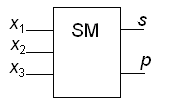
Рисунок 21 – Схема к примеру 2
Сумматор выполняет функции
![]()
Сначала определим наборы для проверки первой функции.
Находим
![]()
Поскольку производная тождественно равна 1, то каждая из входных переменных является существенной на любом наборе других переменных, поэтому любой входной набор является проверяющим.
Для
проверки
![]() надо подать
надо подать
![]() ,
а для проверки
,
а для проверки
![]() надо подать
надо подать
![]() .
.
Минимальными тестами здесь являются пары инверсных наборов
000 – 111, 001 – 110, 011 – 100, 101 – 010,
которые проверяют не только входы, но и выходы сумматора, так как на одном из наборов пары каждый выход равен 1, а на другом 0. Поэтому строить тест для проверки выхода p нет необходимости.
Замечание: Для контроля работоспособности сумматора получен тест минимально возможной длины (два набора). Тест такой же длины получается и для элементов ИСКЛЮЧАЮЩЕЕ ИЛИ и РАВЕНСТВО с нечетным числом входов.
