5.5. Вопросы для самоконтроля
Какова последовательность действий в процессе создания и анализа схемы, реализующей логическую функцию?
Как реализуются логические функции с помощью контактов переключателей и реле? Приведите примеры.
Приведите примеры реализации логических функций на диодах и транзисторах.
Приведите условные графические обозначения типовых логических элементов.
Какова последовательность действий при реализации логической функции на элементах И, ИЛИ, НЕ?
Какова последовательность действий при реализации логической функции на элементах И–НЕ?
Какова последовательность действий при реализации логической функции на элементах ИЛИ–НЕ?
Какова последовательность действий при реализации логической функции, если имеется ограничение на число входов элементов?
Как проводится анализ комбинационной логической схемы?
Как оценивается качество логических схем?
6. Булева производная
6.1. Контроль работоспособности логических схем
Булеву алгебру применяют не только для анализа и синтеза логических схем, но также и для построения контролирующих тестов таких схем.
В простейшем случае проверку работоспособности логической схемы можно провести сравнением на всех возможных наборах входных переменных значений функции, реализуемой схемой, и требуемой. Однако отличия этих функций при наличии в схеме неисправности проявляются только на некоторых наборах входных переменных, а поэтому, с целью экономии времени и средств на проверку работоспособности логической схемы, необходимо знать эти наборы.
Подачу на логическую схему заранее определенной последовательности наборов входных переменных (входных наборов) и анализ ее реакции на эти воздействия называют тестовым контролем.
Совокупность входных наборов, позволяющую определить работоспособность логической схемы, называют контролирующим тестом.
Выбор входных наборов для контроля работоспособности логической схемы осуществляется из тех соображений, чтобы реакции исправной схемы и схемы с любой неисправностью отличались хотя бы на одном наборе. Неисправности, для которых невозможно найти ни одного такого набора, называются необнаруживаемыми.
Неисправность логической схемы – это следствие явлений или действий, вызывающих переход схемы в неисправное состояние. Различают неисправности одиночные и кратные, устойчивые и неустойчивые, произвольные и специальные, детерминированные и стохастические.
Большинство
существующих методов построения тестов
эффективны только при одиночных,
устойчивых, детерминированных
неисправностях вида "константа 1"
и "константа 0". Именно такие
неисправности будут иметься в виду в
настоящем пособии (при необходимости
будем обозначать эти неисправности
1
и
0).
У одного логического элемента могут быть константные неисправности четырех видов:
при любом входном наборе сигнал на выходе элемента имеет постоянное значение 1;
при любом входном наборе сигнал на выходе элемента имеет постоянное значение 0;
на каком–либо входе элемента сигнал имеет постоянное значение 1;
на каком–либо входе элемента сигнал имеет постоянное значение 0.
Если элемент имеет n входов и один выход, то количество его возможных одиночных константных неисправностей равно 2(n + 1).
Введем понятие существенной переменной.
Для логического элемента И (рис. 18,а) можно записать
z = a·b·c.
Если положить b = 1 и c = 1, то в соответствии с законами тождественных преобразований булевой алгебры получим
z = a·1·1 = a.
Иными словами, если b = 1 и c = 1, то вход a управляет выходом z.
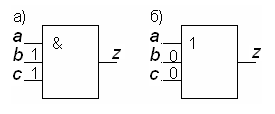
Рисунок 18 – Задание существенных переменных
а) для элемента И, б) для элемента ИЛИ
Для логического элемента ИЛИ (рис. 18,б) имеем
z = a v b v c.
Если здесь положить b = 0 и c = 0 , то получим
z = а v 0 v 0 = a.
То есть, для элемента ИЛИ вход a управляет выходом, если на остальные входы подать значение 0.
Входная переменная логического элемента называется существенной, если она и только она определяет значение выхода этого элемента.
Чтобы некоторую входную переменную элемента И (И–НЕ) сделать существенной, необходимо другим его входным переменным присвоить значения 1 (рис. 18,а).
Чтобы некоторую входную переменную элемента ИЛИ (ИЛИ–НЕ) сделать существенной, необходимо другим его входным переменным присвоить значения 0 (рис. 18,б).
Любая одиночная константная неисправность типа 0 или 1 существенного входа (входа, к которому приложена существенная переменная) или выхода элементов И и ИЛИ может быть обнаружена путем наблюдения значения выхода элемента при подаче на существенный вход значения существенной переменной, обратного значению неисправности.
Неисправности существенного входа элементов И–НЕ, ИЛИ–НЕ могут быть обнаружены при тех же условиях, что и для элементов И и ИЛИ. Неисправности выходов элементов И–НЕ, ИЛИ–НЕ могут быть обнаружены при подаче на существенный вход значений, равных значениям неисправностей.