4.3. Минимизация систем логических уравнений

Логическая схема с m выходами описывается системой m логических уравнений. (Для каждого выхода – свое уравнение.)

Простейший подход к минимизации таких систем уравнений – минимизация каждого уравнения системы в отдельности, но получаемый результат будет далеко не лучшим. Существует несколько, достаточно общих, способов минимизации систем логических уравнений. В основе всех этих способов лежит идея использования одной функции или ее части для получения других функций. Например, пусть заданы функции:

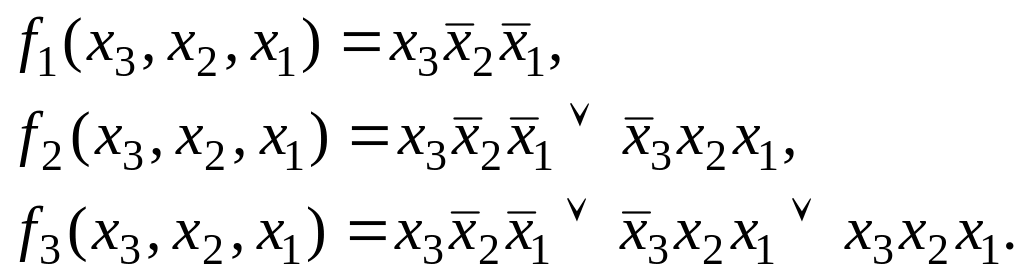
Вполне очевидно, что для минимизации можно использовать соотношения:

что значительно сократит объем необходимого оборудования при реализации.

Удобным и наглядным для минимизации систем логических уравнений является способ с использованием карт Карно.

Применение этого способа покажем на примере.

Пусть даны три функции:

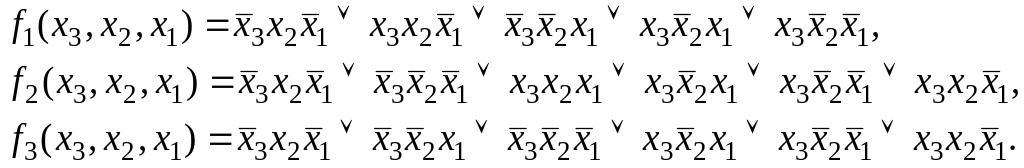
Составим для этих функций карты Карно (табл. 25).

При сравнении карт легко видеть, что функции имеют четыре общих единицы (эти единицы отмечены звездочкой), которые можно выразить некоторой функцией

.

Таблица 25
f1							f2							f3
x3\x2x1	00	01	11	10			x3\x2x1	00	01	11	10			x3\x2x1	00	01	11	10
0	0	1	0	1 *			0	1	0	0	1*			0	1	1	0	1*
1	1*	1*	0	1*			1	1*	1*	1	1*			1	1*	1*	0	1*

С учетом этого выражения функции f₁, f₂, f₃ можно представить следующим образом

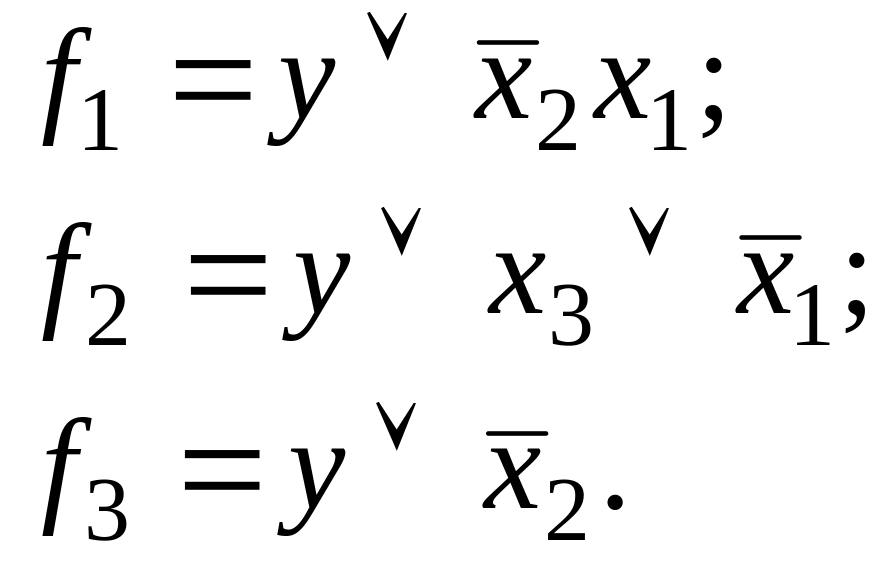
4.4. Частично определенная логическая функция

В табл. 26 приведен пример частично определенной логической функции y, с помощью которой сделана попытка закодировать рабочие дни недели информационно–расчетного центра с учетом видов работы.

Прием посетителей производится по понедельникам, вторникам, четвергам и субботам. В среду и пятницу проводится работа с организациями. Воскресенье – выходной день.

Таблица 26
	№	c	b	a	y	y0	y1	y2	y3
	0	0	0	0	*	0	0	1	1
Пн	1	0	0	1	1	1	1	1	1
Вт	2	0	1	0	1	1	1	1	1
Ср	3	0	1	1	0	0	0	0	0
Чт	4	1	0	0	1	1	1	1	1
Пт	5	1	0	1	0	0	0	0	0
Сб	6	1	1	0	1	1	1	1	1
Вс	7	1	1	1	*	0	1	0	1

Два набора входных переменных 000 и 111 не используются, т.е. они никогда не будут подаваться на устройство кодирования, поэтому функция y на наборах 0 и 7 может принимать любые значения. В графах y₀, y₁, y₂, y₃ табл. 26 показаны все четыре возможных варианта значений этой функции.

Для определения наиболее простого варианта кодирования дней недели проведем минимизацию функций y₀, y₁, y₂, y₃ с помощью карт Карно (см. табл. 27, где звездочкой отмечены доопределенные значения функции).

В результате получаем

,

,

,

.

Как видим, y₂ оказалась самой простой функцией.

Таблица 27
y0 c\ba 00 01 11 10 0 0* 1 0 1 1 1 0 0* 1	y1 c\ba 00 01 11 10 0 0* 1 0 1 1 1 0 1* 1
y2 c\ba 00 01 11 10 0 1* 1 0 1 1 1 0 0* 1	y3 c\ba 00 01 11 10 0 1* 1 0 1 1 1 0 1* 1

Другой пример частично определенной функции дает логический узел ЭВМ – шифратор, таблица истинности которого приведена в табл. 28.

Таблица 28

Входы СD				Выходы CD
y0	y1	y2	y3	a	b
1	0	0	0	0	0
0	1	0	0	0	1
0	0	1	0	1	0
0	0	0	1	1	1

Шифратор (полный) имеет в общем случае 2ⁿ входов и n выходов и выполняет преобразование единичных сигналов на отдельных входах в двоичные наборы на выходах. При 2ⁿ входах возможно входных наборов, а используется только 2ⁿ набора, поэтому функции на выходах шифратора являются частично определенными. Например, при n = 2, когда число входов равно 4 (входы y_i), выходные функции a и b определены только на четырех наборах из 16 возможных.

Формулы для выходных функций a и b определяются по картам Карно, показанным в табл. 29 и табл. 30.

В картах Карно не используемые наборы помечены символом *, а в выделенных прямоугольниках символы * заменяются 1.

Таблица 29

a
y0y1\y2y3	00	01	11	10
00	*	1	1*	0
01	1	1*	1*	1*
11	1*	1*	1*	1*
10	0	1*	1*	*

Таблица 30

b
y0y1\y2y3	00	01	11	10
00	*	1	1*	1
01	0	1*	1*	1*
11	*	1*	1*	1*
10	0	1*	1*	1*

Рекомендация: Если имеем дело с частично определенной функцией, то на наборах, на которых функция не определена, можно ставить либо «0», либо «1», и выбирать вариант, при котором функция получается самой простой. Причем заключение о лучшем варианте, как правило, можно сделать непосредственно по картам функций, не составляя выражений для функций.