3.3. Вопросы для самоконтроля
Что такое – функционально полная система логических операций (функций)? Приведите пример.
Что такое базис? Минимальный базис?
Как можно доказать полноту системы логических функций?
Как можно исключить «лишние» функции из заданной системы функций?
Какие классы логических функций Вы знаете? В чем заключается особенность логических функций, принадлежащих одному классу?
Какие логические функции не сохраняют 0 и 1? Приведите пример.
Поясните понятия двойственной и самодвойственной логической функции. Приведите примеры.
Приведите примеры монотонной и немонотонной логической функции.
Какой особенностью обладают монотонные функции?
Какими свойствами обладает операция Сложение по модулю 2?
Поясните понятие линейной и нелинейной логической функции.
Какие способы преобразования логических функций в полином Жегалкина Вы знаете? Приведите примеры. Какому способу Вы отдали бы предпочтение и почему?
4. Минимизация логических функций
Существует достаточно много методов минимизации логических функций, приведем только два метода, которые чаще всего применяются в инженерной практике:
расчетный;
карт Карно.
4.1. Расчетный метод
Здесь применяют:
– склеивание,
– поглощение,
– развертывание.
4.1.1. Склеивание
а) Если в выражении встречается сумма двух конъюнкций, в одной из которых одна из переменных стоит в прямом значении, а в другой в инверсном значении, а остальные переменные одинаковые, то эту сумму конъюнкций, можно заменить одной конъюнкцией, не содержащей переменную, имеющую разные значения:
Конъюнкции, отличающиеся только значениями одной переменной (в одну из них переменная входит без отрицания, а в другую с отрицанием), называются соседними.
Замечание: Это правило основано на законе дополнительности
и дистрибутивном законе конъюнкции относительно дизъюнкции (п. 1.6, 8,а)
.
б) Если в выражении встречается произведение двух дизъюнкций, в одной из которых одна из переменных стоит в прямом значении, а в другой в инверсном значении, а остальные переменные одинаковые, то это произведение дизъюнкций, можно заменить одной дизъюнкцией, не содержащей переменную, имеющую разные значения:
.
Дизъюнкции, отличающиеся только значениями одной переменной (в одну из них переменная входит без отрицания, а в другую с отрицанием), называются соседними.
Замечание: Это правило основано на законе дополнительности
и дистрибутивном законе дизъюнкции относительно конъюнкции (п. 1.6, 8,б)
.
в) Правила обобщенного склеивания.
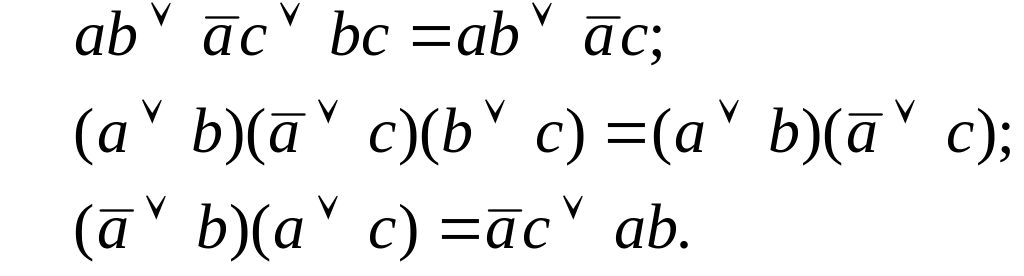
В первом случае исчезло произведение bc, во втором исчезает сумма b c, в третьем снова произведение bc (третий случай после раскрытия скобок сводится к первому). Доказываются эти правила, как обычно, составлением и сравнением таблиц истинности для левой и правой части или с помощью развертывания (см. п. 4.1.3).
4.1.2. Поглощение
а) Если в выражении встречается сумма двух произведений, одно из которых является частью другого, то эту сумму можно заменить меньшим произведением:
.
б) Если в выражении встречается произведение двух сумм, одна из которых является частью другой, то это произведение сумм можно заменить меньшей суммой:
a(a b) = a; a(a b)(a c)…= a; (a b)(a b c)= a b.