Основные параметры сетевой модели реализации проекта
В качестве информационной динамической модели, отображающей процесс выполнения комплекса работ в рамках реализуемого проекта и его конечные цели, используется сетевая модель, в которой весь комплекс операций расчленяется на отдельные, четко определенные операции (работы), располагаемые в строгой технологической последовательности. Сетевой график представляет собой изображение на плоскости хода выполнения проекта.
Ход выполнения проекта можно изобразить на плоскости, используя два основных элемента сетевого графика: стрелки, которыми изображаются работы, и кружочки или квадраты, которыми изображаются события, являющиеся результатом выполнения одной или нескольких работ (рис. 1).
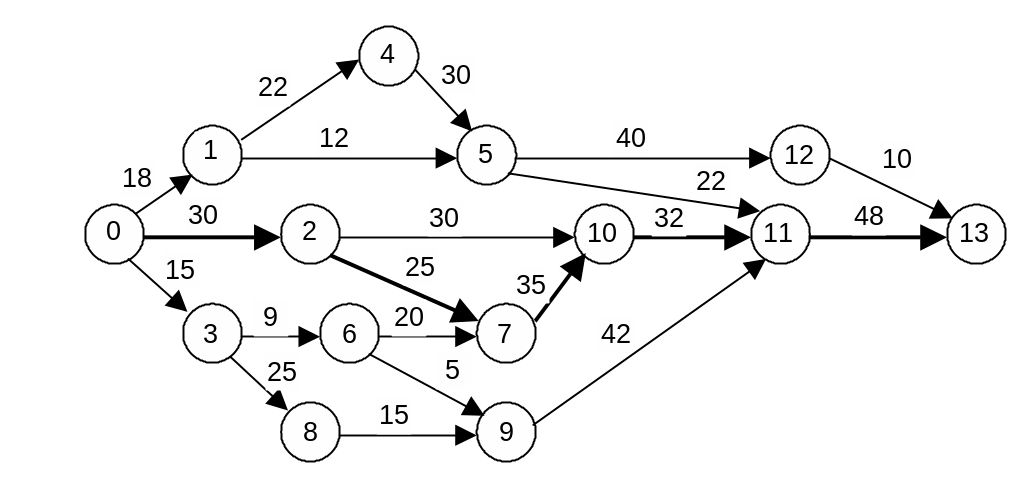
Рис. 1. Пример укрупненного сетевого графика проекта.
Необходимо отметить, что события являются понятиями, не имеющими протяженности во времени, в то время как работы имеют во времени определенную продолжительность7. Например, работа может представлять собой проектирование какого-либо сооружения или системы, выполнение экономических расчетов, обследование объекта, экспертную оценку полученных результатов и т. п.
Термин «работа» может иметь следующие значения:
а) действительная работа в прямом смысле слова, то есть трудовой процесс, требующий затрат времени и других ресурсов;
б) ожидание, не требующее затрат труда, но занимающее некоторое время (например, процесс затвердения бетона);
в) «фиктивная» работа, то есть логическая связь между двумя или несколькими операциями, не требующая затрат ни времени, ни ресурсов, но указывающая, что возможность начала одной работы непосредственно зависит от результатов другой.
Обычно действительные работы изображаются на сетевом графике сплошными стрелками, а «фиктивные» - пунктирными.
Необходимо различать частные результаты отдельных работ и суммарный результат нескольких работ, стрелки которых сходятся в одной точке. Конечный результат любой работы важен не только как факт, удостоверяющий ее окончание, но и как необходимое условие для появления возможности начать следующую за ней работу.
Если какая-либо работа может быть начата только после окончания нескольких определенных работ, то необходимым и достаточным исходным условием для ее начала является лишь сумма частных результатов этих работ, то есть их суммарный результат, который в сетевом планировании и управлении принято называть термином событие. В отдельных случаях событие может совпадать с частным результатом какой-либо одной работы (рис. 1).
Любая стрелка (i, j) сетевого графика опирается своими концами на два кружочка: основанием - на кружок, изображающий событие i, непосредственно предшествующее данной работе, а острием - на кружок, изображающий событие j, непосредственно следующее за данной работой. Всем событиям присваивается определенный шифр (цифровой номер). Таким образом, всякая работа на сетевом графике может быть закодирована шифрами, состоящими из номеров непосредственно ей предшествующего и следующего за ней события.
Никакое событие не может наступить прежде, чем свершатся все события, непосредственно ему предшествующие, и будут выполнены все работы, обозначенные стрелками, соединяющими его с этими событиями.
В сети всегда существуют по крайней мере одно исходное и одно завершающее события. Определение исходного события представляет собой формулировку условия для начала работ по выполнению данного комплекса операций.
Особенность исходного события состоит в том, что оно не является следствием или результатом ни одной из работ, входящих в эту сеть, то есть в данной сети оно не имеет предшествующих работ и событий. Поэтому на сетевом графике в него не входит ни одна стрелка. Исходное событие принято обозначать буквой I.
Определение завершающего события представляет собой формулировку конечной цели комплекса операций, его особенность состоит в том, что оно не является условием начала ни одной из работ, входящих в данную сеть, т. е. в сети оно не имеет последующих за ним работ и событий. Поэтому на сетевом графике из него не выходит ни одна стрелка. Завершающее событие обозначается буквой С.
У каждого события сети, кроме исходного и завершающего, имеется по крайней мере одна непосредственно предшествующая работа и одна непосредственно за ним следующая.
В составленном сетевом графике каждая работа, помимо определения, характеризующего ее содержание, должна иметь также количественные оценки или показатели, характеризующие ее длительность, объем, стоимость и т. д. Круг необходимых показателей работ устанавливается в зависимости от того, какой параметр при реализации инвестиционного проекта является объектом планирования и контроля. Так, например, если ставится целью планирование и контроль лишь календарных сроков работ по созданию нового предприятия, то используется только показатель продолжительности работ.
Все сетевые модели, или просто сети, как их обычно называют, подразделяются на детерминированные и стохастические.
В детерминированной модели все работы имеют фиксированные оценки, которые при определении параметров сети остаются неизменными. Если же некоторые входящие в сеть работы носят случайный характер, то такие оценки в детерминированной сети называются случайными.
Расчет параметров стохастических сетей существенно усложняется по сравнению с детерминированными. Однако этот расчет можно свести к расчету параметров детерминированных сетей, получаемых из рассматриваемой стохастической сети с помощью метода статистических испытаний, иначе говоря, для решения практических задач параметры детерминированных сетей со случайными оценками и стохастических сетей приводят к виду детерминированных сетей с детерминированными оценками. Рассмотрим, как проводится анализ детерминированных сетей с детерминированными оценками.
Если в сети имеется работа (i, j), то мы говорим, что вершина i непосредственно предшествует вершине j, а вершина j непосредственно следует за вершиной i.
Последовательность работ в сети (i1, i2), (i2, i3), … , (ik-1, ik), в которой конечное событие каждой работы совпадает с начальным событием следующей за ней работы, называется путем.
Так как путь полностью определяется событиями, через которые он проходит, будем для краткости обозначать его перечислением событий, которые лежат на нем (i1, i2, i3, … , ik-1, ik).
Стрелки на графике располагаются в таком порядке, что они изображают логическую последовательность выполнения отдельных работ, тем самым определяя направление перехода от одного события к другому или очередность свершения событий на данном пути.
Необходимо различать четыре вида пути:
а) путь, начало которого совпадает с исходным событием сети, а конец - с завершающим событием сети, является полным путем и обозначается буквой L (для краткости его называют просто путь);
б) путь, ведущий к какому-либо событию i от исходного события сети, называется путем, предшествующим событию i, и обозначается через L(I – i);
в) путь, ведущий от какого-либо события i к завершающему событию сети, называется путем, следующим за событием i, и обозначается через L(i – C);
г) путь, соединяющий какие-либо два события in и im, не являющиеся исходным и завершающим событиями сети, называется путем между событиями in и im и обозначается через l(in, im).
При построении сетевых графиков необходимо соблюдать следующие правила.
1. В сети не должно быть тупиков, то есть событий, из которых не выходит ни одной работы, если только эти события не являются для данной сети завершающими.
Наличие тупиков в сети, как правило, указывает на то, что либо связь отсутствует ошибочно, либо результат работы или работ, непосредственно предшествующих этому событию, никому из исполнителей данного комплекса операций не нужен. Следовательно, тупиковые работы являются лишними и могут быть аннулированы.
2. В сети не должно быть событий, в которые не входит ни одной работы, если только эти события не являются для данной сети исходными.
3. В сети не должно быть замкнутых контуров, то есть не должно быть путей, соединяющих какое-либо событие с ним же самим.
Наличие замкнутых контуров указывает на случайную или логическую ошибку, допущенную при построении сети. При обнаружении подобной ошибки сеть после соответствующей проверки должна быть исправлена.
4. В сети не должно быть работ, имеющих одинаковые шифры, то есть работ с общими начальным и конечным событиями.
Обозначим через t(i, j) продолжительность работы (i, j).
Продолжительность любого пути равна суммарной продолжительности составляющих его работ и обозначается через t(L).
Например, в сетевом графике на рис. 1 продолжительность пути L1 = (0, 1, 4, 5, 11, 13) равна
T(L1) = t(0, 1) + t(1, 4) + t(4, 5) + t(5, 11) + t(11, 13) = 18 + 22 + 30 + 22 + 48 = 140 дням.
Всего в рассматриваемом сетевом графике девять путей. В табл. 1 для каждого из путей указаны перечень составляющих его работ и продолжительность.
Т а б л и ц а 1