
- •Элементы теории вероятностей и математической статистики
- •Содержание
- •Введение
- •Элементы комбинаторики
- •Пример. Из семи заводов организация должна выбрать три для размещения трех различных заказов. Сколькими способами можно разместить заказы?
- •Пример. 6 человек из 15 можно выбрать числом способов, равным
- •Пример. Если из текста задачи 3 убрать условие различия трех заказов, сохранив все остальные условия, получим другую задачу.
- •Пример. Сколько четырехзначных чисел можно составить из цифр 0,1,2,3,4,5, если:
- •Пример. Новый президент банка должен назначить двух новых вице-президентов из числа десяти директоров. Сколько способов существует у президента, если:
- •Элементы теории вероятностей
- •§ 1. Предмет теории вероятностей
- •§ 2. Случайные события
- •Так как , то , каково бы ни было по своей природе событие а.
- •Если а - событие невозможное, то .
- •Если в- событие достоверное, то .
- •§ 3. Случайные величины и их характеристики
- •Сводная таблица характеристик законов распределения дискретных случайных величин
- •Сводная таблица характеристик законов распределения непрерывных случайных величин
- •§ 4. Двумерные случайные величины
- •§ 5. Закон больших чисел Центральная предельная теорема
- •Элементы математической статистики
- •§ 1. Предмет математической статистики
- •§ 2. Выборочная совокупность и ее характеристики
- •§ 3. Законы распределения выборочных характеристик
- •§ 4. Статистическое оценивание числовых характеристик случайной величины и ее закона распределения
- •§ 5. Статистические гипотезы
- •§ 6. Методы регрессионного и корреляционного анализа
- •Количественные критерии оценки тесноты связи (шкала Чеддока)
- •Контрольные задания Вариант 1
- •Рекомендуемая литература
- •Критические точки распределения χ2
- •Критические точки распределения Стьюдента
- •Критические точки распределения Фишера-Снедекора
- •Элементы теории вероятностей и математической статистики
- •192171, Г. Санкт-Петербург, ул. Седова, 55/1
§ 3. Случайные величины и их характеристики
Число отличных оценок, которые студенты одной учебной группы получат в ближайшую сессию, может быть различным. Оно может быть равным 0 (нет ни одной отличной оценки), 1, 2 и т.д. до некоторого конечного числа n. К величинам такого же типа относятся, например: вес корнеплода свеклы на участке, дальность полета артиллерийского снаряда, количество бракованных деталей в партии и т.д. Общим для них является то, что каждая величина может принимать некоторые значения, но нельзя достоверно предсказать какое именно значение она примет в рассматриваемом опыте, явлении, наблюдении. Эти величины характеризуют все возможные результаты испытания с количественной стороны.
Случайной называется величина, которая в результате испытания принимает одно и только одно возможное значение, заранее неизвестное.
Случайная величина называется дискретной (прерывной), если все ее возможные значения можно перенумеровать, т.е. Х – это случайная величина, принимающая значения из конечного или счётного множества.
Случайная величина называется непрерывной, если все ее возможные значения заполняют некоторый конечный или бесконечный интервал.
Пример. Число студентов на лекции – дискретная случайная величина, продолжительность лекции – непрерывная.
Случайные величины обозначаются заглавными буквами латинского алфавита X, Y, Z, а их возможные значения - соответствующими прописными буквами, то есть x1, x2,..., xn и т.д.
Законом распределения случайной величины называется соответствие, устанавливающее связь между возможными значениями случайной величины и их вероятностями.
Закон распределения может быть задан
аналитически,
таблично,
графически.
Закон распределения дискретной случайной величины задаётся чаще всего рядом распределения, т.е. таблицей
X |
x1 |
x2, |
… |
xn |
P |
P1 |
p2 |
… |
pn |
в
которой x1,
x2,...,
xn
– расположенные по возрастанию значения
дискретной случайной величины
![]() ,
а p1,
p2,
…, pn
– соответствующие этим значениям
вероятности. Число столбцов в этой
таблице может быть конечным (если
соответствующая случайная величина
принимает конечное число значений) или
бесконечным. То, что случайная величина
Х
принимает одно из значений х1,
х2,
… ,
хn,
является достоверным событием и поэтому
выполняется равенство
,
а p1,
p2,
…, pn
– соответствующие этим значениям
вероятности. Число столбцов в этой
таблице может быть конечным (если
соответствующая случайная величина
принимает конечное число значений) или
бесконечным. То, что случайная величина
Х
принимает одно из значений х1,
х2,
… ,
хn,
является достоверным событием и поэтому
выполняется равенство
 (в случае бесконечной последовательности
значений
(в случае бесконечной последовательности
значений
![]() ).
).
Пример. Отмечено, что в некоторой местности в течение ряда лет в июне 30% дождливых дней. Составить закон распределения случайной величины X – числа дождливых дней в течение одной недели июня месяца. События, состоящие в том, что в 1-й день недели идет дождь, во 2-й - дождь и т.д. считать независимыми.
Решение. Случайная величина X принимает следующие значения:
x1=0, x2=1, x3=2, x4=3, x5=4, x6=5, x7=6, x8=7.
Вероятности этих значений вычислим по формуле Бернулли:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Закон распределения представим в виде таблицы
X |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
P |
0.0824 |
0.2472 |
0.3128 |
0.2263 |
0.0973 |
0.0250 |
0.0036 |
0.0002 |
Наибольшую вероятность имеет событие, состоящее в том, что на неделе будет два дождливых дня.
Однако не все случайные величины могут быть описаны так просто как дискретные случайные величины. Например, время горения электрической лампочки может принимать любое значение от нуля до бесконечности. И если предполагается, что лампочка была в начале исправной, то вероятность того, что время ее службы это есть некоторое точное значение, будет равна нулю. Ненулевыми будут вероятности только сложных событий, например, продолжительность службы лампочки от одного до двух месяцев. В этом случае табличный способ задания случайных величин неприменим, и распределение случайной величины полностью определяется ее функцией распределения.
Функция распределения в точке x – это вероятность того, что случайная величина X примет значение, меньшее заданного числа x:
![]() .
.
Из определения следуют следующие свойства:
Как любая вероятность
 .
.F(x) – неубывающая функция, т.е. если х1< х2, то F(x1)≤ F(x2).
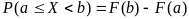 -
вероятность попадания в интервал.
-
вероятность попадания в интервал.Если все возможные значения случайной величины Х находятся на интервале (а, b), то F(x)=0 при х≤а и F(x)=1 при
 .
. ,
,
 .
.
Исходя из определения функции распределения можно дать другое определение непрерывной случайной величины: случайная величина, принимающая вещественные значения, называется непрерывной, если ее функция распределения непрерывна.
В
этом случае вероятности событий связанных
с данной случайной величиной, можно
выразить через функцию
плотности вероятности, которая
является производной от функции
распределения:
![]() .
Часто по условию задачи задают плотность
распределения (дифференциальная
функция), зная которую можно вычислить
по формуле Ньютона-Лейбница и функцию
распределения (интегральную):
.
Часто по условию задачи задают плотность
распределения (дифференциальная
функция), зная которую можно вычислить
по формуле Ньютона-Лейбница и функцию
распределения (интегральную):
![]() .
.
Согласно пятому свойству для F(x) имеем
![]() .
.
Последнее равенство называется условием нормировки функции плотности f(x).
Пример. Плотность распределения случайной величины X равна
![]() .
.
Найти A, F(x) и вероятность P(0.5X1.5).
Решение. Для нахождения А запишем условие нормировки

Если
x<0,
то
![]() .
.
Если
![]() ,
то
,
то
![]()
Если
x>2,
то
 .
.
Итак,
 .
.
Наконец, P(0.5X1.5)=P(X<1.5)+P(X=1.5)-P(X<0.5)=F(1.5)+0-F(0.5)=
![]()
Составить полное представление о случайной величине только по закону распределения часто бывает трудно. Поэтому возникает необходимость характеризовать случайную величину с помощью некоторых постоянных величин. Они выводятся на основе ее закона распределения. Прежде всего к ним относится математическое ожидание - важнейшая «характеристика положения» случайной величины.
Математическое ожидание - это число, которое выражает среднее значение случайной величины с учетом распределения.
Для дискретных величин она вычисляется по формуле
![]() ,
,
где x1, x2,...,xn,... – возможные значения случайной величины,
p1, p2,,...,pn,...– их вероятности.
Для непрерывных случайных величин математическое ожидание определяется формулой
![]() .
.
Свойства математического ожидания:
M(C)=C (С=const);
M(CX)=CM(X) (С=const);
M(X+Y)=M(X)+M(Y);
M(XY)=M(X)M(Y) (для независимых случайных величин).
Пример. Пусть в некотором магазине, торгующем электробытовой техникой, получены статистические данные о количестве проданных холодильников в каждый день месяца (условно считаем, что месяц состоит из 30 рабочих дней). Эти данные представлены в таблице
Количество проданных холодильников |
0 |
1 |
2 |
3 |
4 |
5 |
Число дней, за которые было продано данное число холодильников |
3 |
7 |
8 |
9 |
2 |
1 |
По этой таблице легко подсчитать число холодильников, проданных в магазине за месяц: 0·1+1·7+2·8+3·9+4·2+5·1 = 63. Чтобы подсчитать среднее число холодильников, продававшихся в один день месяца, нужно эту сумму разделить на 30, в результате получим 2.1. Если в приведенной таблице каждое число второй строки поделить на 30, то получится последовательность дробей
![]() ,
,
каждая дробь представляет собой так называемую относительную частоту, с которой в данный месяц появлялся приведенный в верхней строке объём продаж. Очевидно, что если просуммировать все произведения чисел, стоящих в первой строке таблицы, на их относительные частоты, то получится то же среднее число продававшихся в один день холодильников:
![]() .
.
Если бы в последней формуле относительные частоты рассчитывались не для одного месяца, а для существенно большего срока, то при некоторых условиях (например, при отсутствии кризисных явлений, существенно влияющих на спрос населения на дорогостоящие товары) эти относительные частоты можно было бы считать довольно близкими к вероятностям соответствующих значений объёма продаж. Таким образом, приходим к выводу, что математическое ожидание случайной величины – это в некотором смысле её среднее значение.
Характеристиками рассеивания возможных значений случайной величины вокруг математического ожидания служат, в частности, дисперсия и среднеквадратичное отклонение.
Дисперсией
случайной
величины Х
называется математическое ожидание
квадрата отклонения значений величины
от ее математического ожидания:
![]() .
.
Для дискретных величин она определяется по формуле
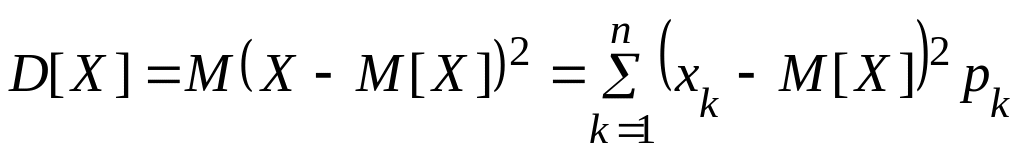 .
.
При практических вычислениях используют формулу
![]() .
.
Для непрерывных случайных величин дисперсия определяется формулой
![]() .
.
Вычислительная формула для D(X):
![]() .
.
Дисперсия характеризует меру рассеяния возможных значений случайной величины около ее математического ожидания. Из двух величин с равными математическими ожиданиями та считается «лучшей», которая имеет меньший разброс.
Свойства дисперсии:
D(C)=0 (С=const);
D(CX)=C2D(X) (С=const);
D(XY)=D(X)+D(Y) (для независимых случайных величин).
Корень квадратный из дисперсии случайной величины называется средним квадратическим отклонением и обозначается (X) или x:
![]() .
.
Пример. Случайная величина X распределена по следующему закону:
-
X
1
2
3
P(X)
0.2
0.3
0.5
Найти M(X) и D(X).
Решение.
M(X)=10.2+20.3+30.5=2.3.
Для вычисления дисперсии составим закон распределения X2:
-
X2
1
4
9
P(X)
0.2
0.3
0.5
M(X2)=10.2+40.3+90.5=5.9.
=5.9-(2.3)2=0.61.
Такая характеристика случайной величины, как математическое ожидание, называется иногда характеристикой положения, так как она дает представление о положении случайной величины на числовой оси. Другими характеристиками положения являются мода и медиана.
Модой М0[X] называется значение случайной величины Х, при котором плотность распределения f(x) имеет наибольшее значение – для непрерывной случайной величины, а для дискретной – мода это значение случайной величины, соответствующее большей вероятности.
Медианой Ме[X] непрерывной случайной величины Х, называют ее значение, определяемой равенством
![]()
или
![]() .
.
Для случайных величин существует несколько наиболее распространенных распределений, характеристики которых приведены в таблице.
