Пример. Из семи заводов организация должна выбрать три для размещения трех различных заказов. Сколькими способами можно разместить заказы?

Решение. Так как все заводы различны, и из условия ясно, что каждый завод может либо получить один заказ, либо не получить ни одного, то в этом случае нужно подсчитать число размещений:

.

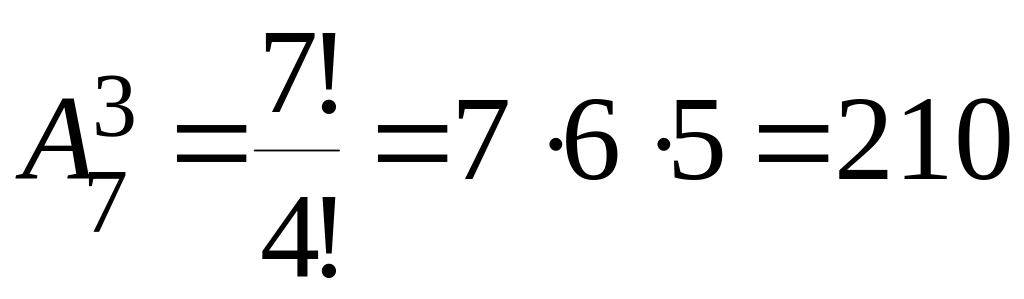Сочетаниями называют комбинации, составленные из n различных элементов по m элементов, которые отличаются хотя бы одним элементом. Число сочетаний вычисляется по формуле:

.

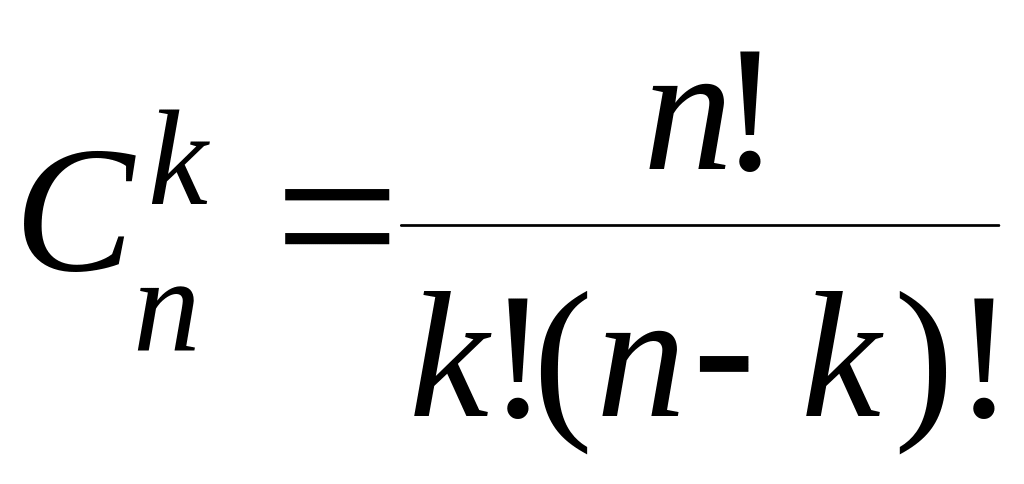Пример. 6 человек из 15 можно выбрать числом способов, равным

.

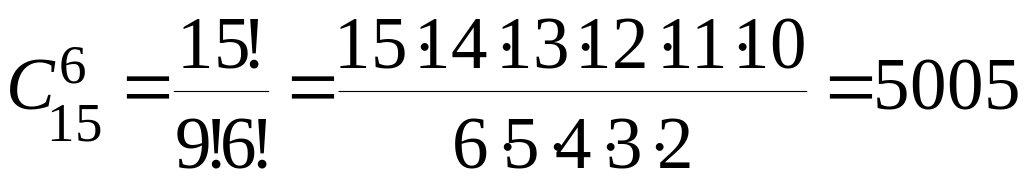Пример. Если из текста задачи 3 убрать условие различия трех заказов, сохранив все остальные условия, получим другую задачу.

Решение. Теперь способ размещения заказов определяется только выбором тройки заводов, так как все эти заводы получат одинаковые заказы, и число вариантов определяется как число сочетаний:

.

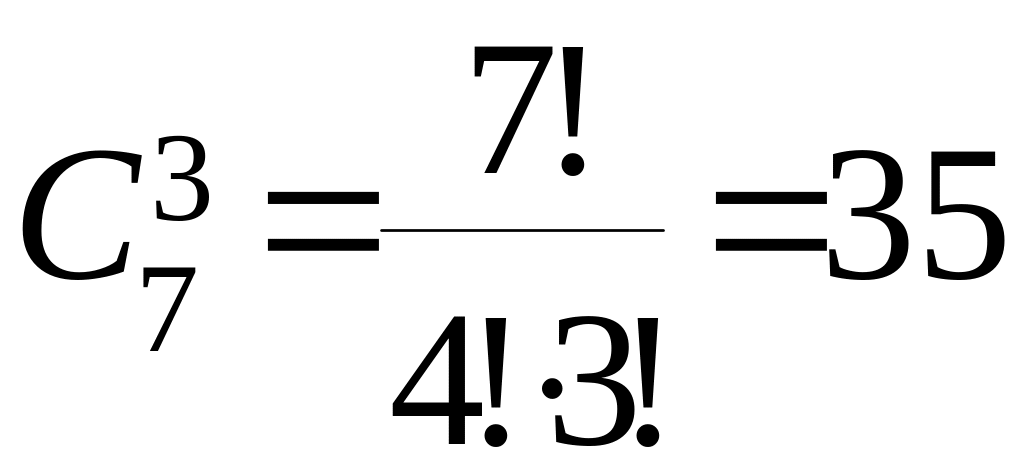Замечания. 1). Числа размещений, перестановок и сочетаний связаны равенством:

.

2). Выше предполагалось, что все n элементов различны. Если же некоторые элементы повторяются, то в этом случае комбинации с повторениями вычисляют по другим формулам. Например, если среди n элементов есть n₁ элементов одного вида, n₂ элементов другого вида и т.д., то число перестановок с повторениями вычисляется по формуле:

P_n (n1, n2, ...) = n! / (n1! n2! ... ), где n1 + n2 + ... = n.

Ниже в таблице приводятся формулы для подсчета числа элементов в различных соединениях

Виды комбинаций		Формулы
Перестановки	Без повторений
	С повторениями
Размещения	Без повторений
	С повторениями
Сочетания	Без повторений
	С повторениями

Сформулируем два универсальных правила, применяемых при решении комбинаторных задач.

Правило суммы. Если некоторый объект А может быть выбран из совокупности объектов m способами, а другой объект В может быть выбран n способами, то выбрать либо А, либо В можно (m + n) способами.

Пример. Если на одной полке книжного шкафа стоит 30 различных книг, а на другой - 40 различных книг (не таких, как на первой полке), то выбрать одну книгу из стоящих на этих полках можно 30+40=70 способами.

Правило произведения. Если объект А можно выбрать из совокупности объектов m способами и после каждого такого выбора объект В можно выбрать n способами, то пара объектов (А, В) в указанном порядке может быть выбрана mn способами.

Пример. Сколько четырехзначных чисел можно составить из цифр 0,1,2,3,4,5, если:

а) ни одна цифра не повторяется больше одного раза в записи числа;

б) цифры в записи числа могут повторяться;

в) цифры могут повторяться в записи числа, но число должно быть нечетным.

Решение. а) Первой цифрой при этом может быть любая из 5 цифр 1,2,3,4,5 (0 не может быть первой цифрой, потому что в таком случае число не четырехзначное). Если первая цифра выбрана, то вторая может быть выбрана 5 способами, третья — 4 способами, четвертая — 3 способами. Согласно правилу произведения общее число способов равно 5∙5∙4∙3=300.

б) Для первой цифры имеем 5 возможностей (1,2,3,4,5), для каждой из следующих цифр — 6 возможностей (0,1,2,3,4,5). Следовательно, общее количество чисел равно 5∙6∙6∙6=1080.

в) Первой цифрой может быть одна из 5 цифр 1,2,3,4,5, а последней 1,3,5. Следовательно, общее количество чисел равно 5∙6∙6∙3=540.

Пример. Маша поссорилась с Петей и не хочет ехать с ним в одном автобусе. От общежития до института с 7 до 8 ч отправляется пять автобусов. Неуспевший на последний из этих автобусов опаздывает на лекцию. Сколькими способами Маша и Петя могут доехать до института в разных автобусах и не опоздать на лекцию?

Решение. Петя может доехать до института =5 различными способами (на одном из пяти автобусов), при этом Маше остаётся только =4 способа (так как один из автобусов занят Петей). Таким образом, по правилу произведения у Пети и Маши есть различных способов добраться до института в разных автобусах и не опоздать на лекцию.

Пример. В информационно-технологическом управлении банка работают три аналитика, десять программистов и 20 инженеров. Для сверхурочной работы в праздничный день начальник управления должен выделить одного сотрудника. Сколькими способами он это может сделать?

Решение. Начальник управления может отобрать одного аналитика n₁=3 способами, одного программиста — n₂=10 способами, а одного инженера — =20 способами. Поскольку по условию задачи начальник управления может выделить любого из своих сотрудников, согласно правилу суммы у него существует различных способа выбрать сотрудника для сверхурочной работы.