§ 3. Законы распределения выборочных характеристик

После получения вариационного ряда как выборочного распределения возникает первая задача – найти на основе этого распределения общий закон распределения для данного признака. На основе всестороннего анализа имеющегося распределения и изучения рассматриваемого признака выбирают из известных распределений определенный закон распределения в качестве предполагаемого теоретического закона распределения для рассматриваемого признака в генеральной совокупности.

Рассмотрим несколько распределений, которые имеют важные статистические приложения:

• нормальное распределение,

• ²-распределение (распределение Пирсона),

• t-распределение (распределение Стьюдента),

• F-распределение (распределение Фишера).

а) Нормальный закон распределения случайной величины. Нормальное распределение рассмотрено впервые А. Муавром в I733 г., а в I809 г. открыто независимо от исследований А. Муавра К. Гауссом. Распределение Муавра - Лапласа - Гаусса занимает ведущее место в теории и практике вероятностно-статистических исследований.

Как уже было введено в разделе «Теория вероятностей», нормальным называется распределение, имеющее вид:

.

По этой формуле при различных значениях среднего арифметического ( ) и среднеквадратичного отклонения ( ) получается семейство нормальных кривых. Нормальное распределение симметрично относительно и имеет следующие числовые характеристики: математическое ожидание a= , дисперсия , коэффициент асимметрии Аs=0, неприведенный коэффициент эксцесса Е_х = 3, приведенный коэффициент эксцесса γ = 0.

Для нормального распределения значения моды, медианы и среднего арифметического равны между собой.

При решении статистических задач во многих случаях применяется стандартное нормальное распределение (единичное, нормальное). Оно получается при условии, что и , т.е. имеет параметры (0,1). Использование стандартного нормального распределения позволяет анализировать любое нормальное распределение на основе характеристик единичного нормального распределения.

б) Распределение (распределение К. Пирсона). Пусть – независимые нормально распределенные случайные величины с параметрами (0,1). Распределение случайной величины

называется распределением хи-квадрат с п степенями свободы, а сама величина – случайной величиной хи-квадрат с п степенями свободы.

Заметим, что количество степеней свободы п является единственным параметром хи-квадрат распределения и значения неотрицательны, т.е. .

При больших значениях п распределение случайной величины близко к нормальному распределению с параметрами . Однако при малых значениях п функция плотности случайной величины значительно отличается от кривой нормального распределения.

На рис. 3.1 показаны плотности распределения случайной величины при и . Видно, что при увеличении плотность «приближается» к плотности нормального распределения.

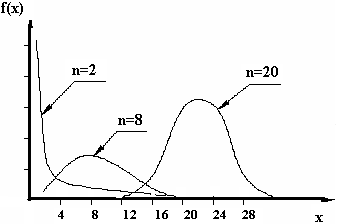
Рис. 3.1. Плотность распределения χ-квадрат

Сумма независимых случайных величин также распределена по закону хи-квадрат со степенями свободы.

в) Распределение Стьюдента (t-распределение). Если случайная величина z – нормально распределена с параметрами , а величина ω имеет –распределение с к степенями свободы, то величина

распределена по закону Стьюдента с k степенями свободы и называется t-распределением. Это распределение впервые в 1908 году было использовано английским математиком В.Госсетом, который подписывал свои работы псевдонимом Стьюдент (Студент).

Распределение Стьюдента симметрично относительно нуля (рис.3.2.), и значения t табулированы в зависимости от степеней свободы k и вероятности α.

Рис. 3.2. Плотность распределения Стьюдента

При больших значениях k кривая плотности близка к кривой нормального распределения . Поэтому в практических расчетах при k>30 часто считают, что

.

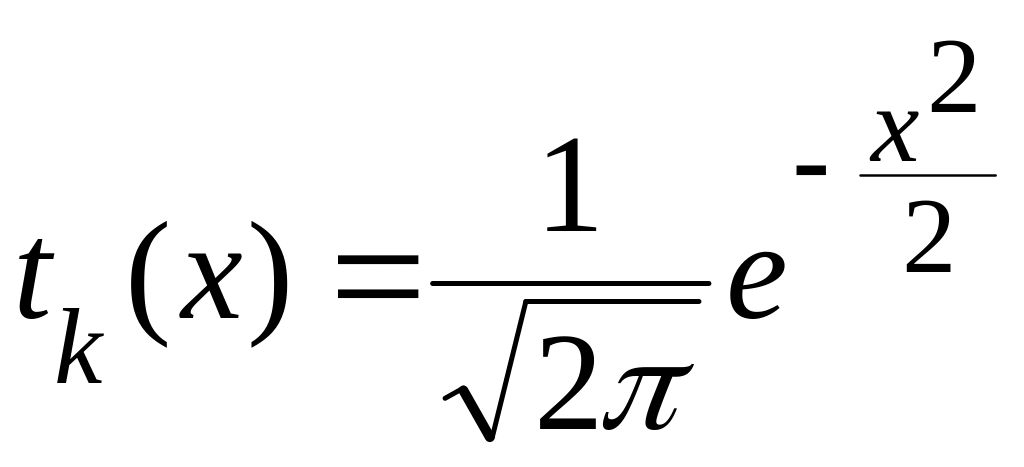г) Распределение Фишера ( -распределение). Пусть и – независимые случайные величины, имеющие хи-квадрат распределения с п и m степенями свободы, соответственно. Распределение случайной величины

называется F-распределением или распределением Фишера с п и m степенями свободы. Так как случайные величины и то .

Дальнейшие рассуждения будут базироваться на теореме о распределении выборочных характеристик и , доказанную Р.Фишером.

Теорема (о распределении выборочных характеристик). Если генеральная совокупность Х распределена по нормальному закону с параметрами и , то:

а) случайная величина распределена нормально с параметрами ,

б) случайная величина имеет распределение ,

в) случайные величины и независимы.

Пусть из генеральной совокупности Х, имеющей нормальный закон распределения с математическим ожиданием и дисперсией , взята случайная выборка объемом n, тогда выборочные характеристики (статистики) будут представлены следующим образом:

1) - имеет нормированный нормальный закон распределения N(0,1) с математическим ожиданием, равным нулю, и дисперсией, равной единице, где - выборочная средняя арифметическая, - среднее квадратическое отклонение;

2) - имеет распределение Стьюдента (t - распределение) с n-1 степенями свободы, где S - выборочное среднее квадратическое отклонение, равное ;

3) - имеет нормированное нормальное распределение N(0,1);

4) - имеет распределение Стьюдента (t-распределение) с n-1 степенями свободы;

5) - имеет распределение (хи-квадрат) с n-1 степенями свободы;

6) В случае двух независимых выборок их нормальных генеральных совокупностей Х и Y c одинаковыми математическими ожиданиями μ_х=μ_у=μ и дисперсиями статистика

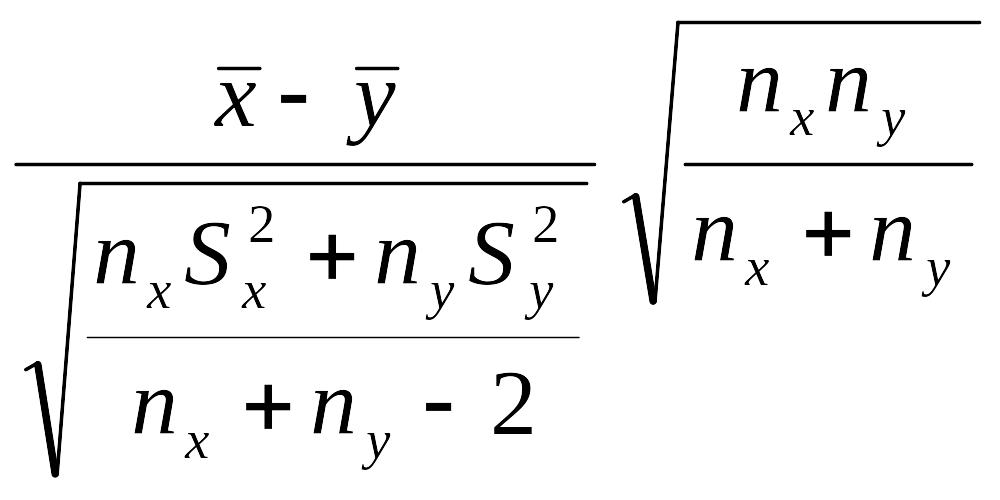– имеет распределение Стьюдента (t - распределение) с (n_х + n_у -2) степенями свободы, где - выборочные средние двух независимых выборок х и у из генеральных совокупностей с одинаковыми, но неизвестными параметрами a и σ; - выборочные дисперсии соответственно первой и второй выборок.

После получения распределения выборки приходим к необходимости рассмотрения двух вопросов:

1) выбрать вид теоретического распределения в качестве предполагаемого для рассматриваемого признака, а затем найти его параметры;

2) проверить правильность сделанного выбора, проверить согласованность имеющегося эмпирического материала с предполагаемым теоретическим распределением признака в генеральной совокупности.