Тест «Понятие производной функции. Правила вычисления производных»

1. Вставьте пропущенные слова так, чтобы получилось верное высказывание: а) Если функции u и v ______________________________в точке x₀, то их сумма ___________________в этой точке и ___________________. б) Дробно – рациональные функции дифференцируемы________________________________________.

2. У кажите истинность и ложность следующих утверждений: а) Если функция дифференцируема в точке , то она непрерывна в этой точке. б) . в) Если , то . г) Если ,то .

3. Какая из функций имеет производную ? Запишите верный ответ. .

4. Н айдите производные функций :

5. Вычислите ,если .

6. Решите уравнение ,если .

7. Решите неравенство ,если .Выберите верный ответ.

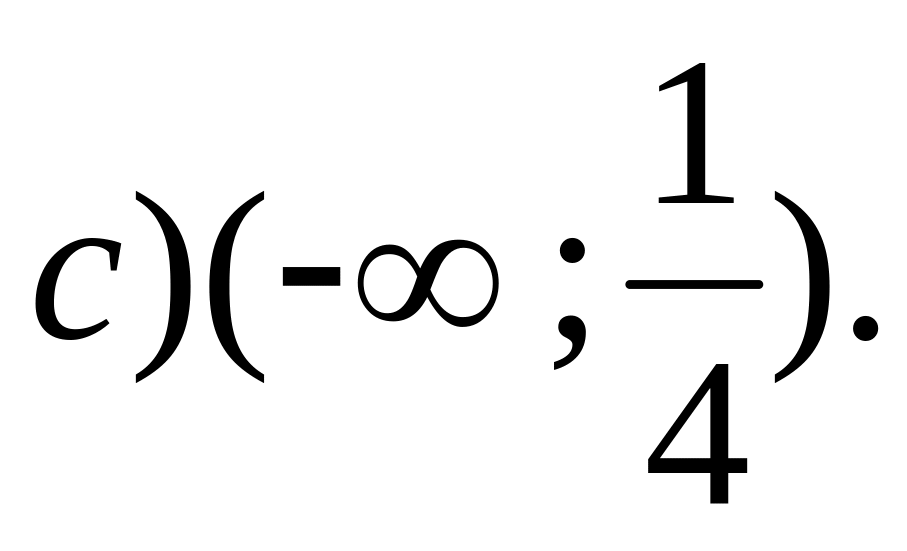
8. Задайте формулой две функции, производные которых равны: ; ; .

9. Определите, при каких значениях выполняется неравенство , если , а .

10. Решите уравнение , если .

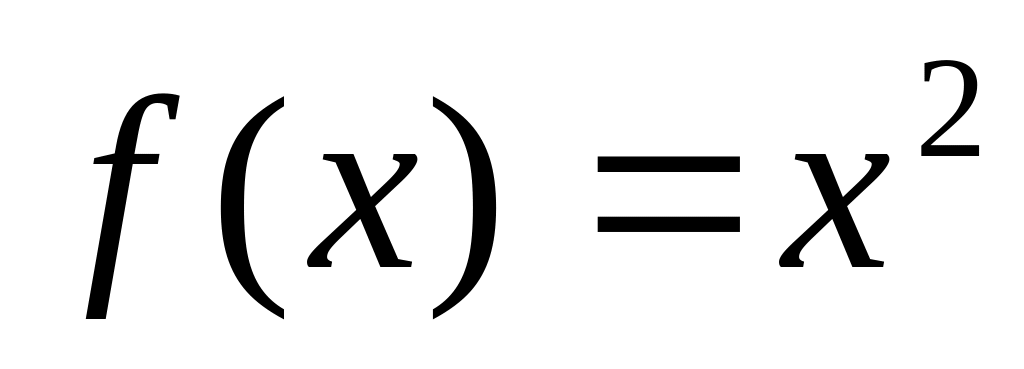Задания для самостоятельного решения.

1. Найдите производную каждой из функций.

2. Вычислите значения производной функции в данных точках.

2.3. Геометрический смысл производной.

Геометрическая интерпретация производной, впервые данная в конце XVII в. Лейбницем, состоит в следующем: значение производной функции в точке равно угловому коэффициенту касательной, проведенной к графику функции в той же точке , т.е. Таким образом, если функция в точке имеет производную, то график этой функции в точке с абсциссой имеет касательную, и, наоборот, если в некоторой точке с абсциссой существует касательная к графику, то при этом значении существует производная. Иначе говоря, существование касательной к кривой в некоторой точке с абсциссой необходимо и достаточно для существования производной в точке .Из данного равенства следует, что для нахождения углового коэффициента касательной к кривой в точке нужно найти производную и подставить в нее вместо абсциссу точки касания: .

Рисунок 5

Пример 13. Найти угловой коэффициент касательной, проведенной к графику функции в точке .

Решение. Найдем производную функции в точке . .

Итак, угловой коэффициент касательной, проведенной к графику функции в точке равен 12.

2.4. Физический смысл производной.

Производная -это скорость изменения функции относительно ее аргумента . Производная характеризует быстроту изменения функции, т.е. скорость роста. Отрицательная скорость роста означает падение – уменьшение при увеличении , т.е. скорость убывания функции. Производная указывает на тенденции, характерные для изменения и позволяет судить о том, что можно ожидать при дальнейшем изменении аргумента.

Мгновенная скорость - - это первая производная от перемещения по времени.

Пример 14. В какой момент времени скорость тела, движущегося по закону , равна 0?

Решение. Скорость тела - это первая производная от перемещения по времени . .

Если , то .