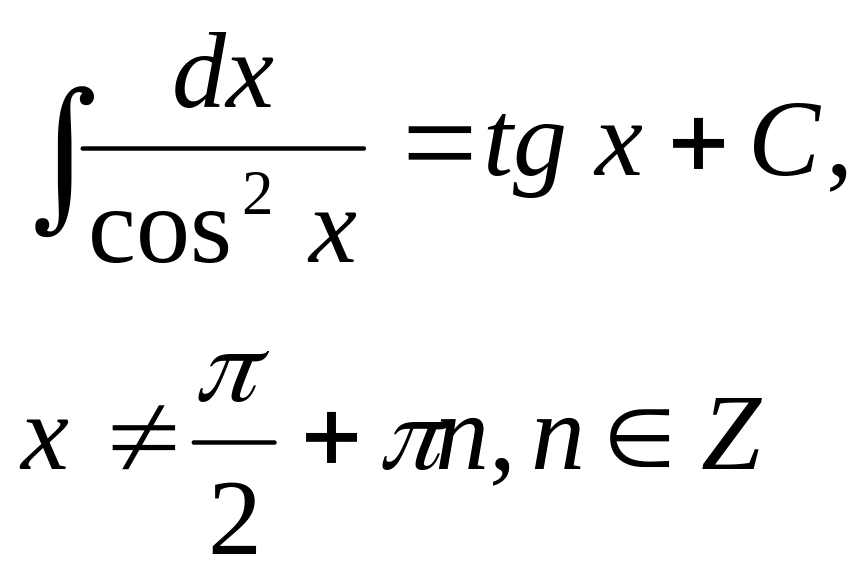- •Учебное пособие по математике для студентов II курса
- •Студенту: как работать с этой книгой.
- •Введение.
- •Раздел 1. Предел и непрерывность функции.
- •1.1 Предел функции
- •1.2.Односторонние (левый и правый) пределы.
- •1.3.Основные теоремы о пределах.
- •1.4.Предел функции на бесконечности.
- •1.5.Способы вычисления пределов функций.
- •1.5.1. Непосредственное вычисление предела функции в точке.
- •Раскрытие неопределенности .
- •2. Способ. Умножение числителя и знаменателя дроби на выражение сопряженное числителю (знаменателю).
- •Раскрытие неопределенности .
- •И спользование замечательных пределов.
- •Контрольные вопросы.
- •Задания для самостоятельного решения.
- •1.6.Непрерывность функции.
- •1.6.1.Свойства непрерывных функций.
- •1.6.2.Точки разрыва функции.
- •1.6.3.Классификация точек разрыва функции.
- •Контрольные вопросы.
- •Задания для самостоятельного решения.
- •Тест «Предел функции в точке. Непрерывность функций»
- •Задания для самостоятельного решения.
- •Контрольное задание.
- •Раздел 2. Производная и ее приложения.
- •2.1.Производная.
- •2.2. Правила вычисления производных.
- •Тест «Понятие производной функции. Правила вычисления производных»
- •Задания для самостоятельного решения.
- •2.3. Геометрический смысл производной.
- •2.4. Физический смысл производной.
- •2.5.Связь между непрерывностью и дифференцируемостью функции.
- •2.6.Производная сложной функции.
- •2.7.Производные высших порядков.
- •2.8. Механический смысл производной второго порядка.
- •Контрольные вопросы.
- •Тест «Геометрический и механический смысл производной. Производная сложной функции».
- •Задания для самостоятельного решения.
- •2.9.Дифференциал функции.
- •2.9.1.Свойства дифференциала.
- •Задания для самостоятельного решения.
- •Контрольное задание.
- •2.10. Применение производной в исследовании функций.
- •2.10.1.Исследование функции на монотонность.
- •2.10.2. Исследование функции на экстремум.
- •2.10.3. Условия выпуклости и точки перегиба графика функции.
- •2.10.4.Асимптоты графика функции.
- •2.10.5. Схема исследования функции.
- •Контрольные вопросы.
- •Тест «Применение производной к исследованию функции»
- •Раздел 3. Интеграл и его приложения.
- •3. 1. 2. Неопределенный интеграл.
- •3. 1. 3. Основные свойства неопределенного интеграла.
- •3. 1. 4. Основные способы интегрирования.
- •Интегрирование по частям.
- •Контрольные вопросы.
- •Тест «Первообразная. Неопределенный интеграл»
- •Задания для самостоятельного решения.
- •3.2.Определенный интеграл.
- •3.2.1.Основные свойства определенного интеграла.
- •3.2.2. Вычисления определенных интегралов.
- •Вычисление определенных с использованием определения.
- •Подстановка в определенном интеграле.
- •Интегрирование по частям.
- •3.2.3. Применение определенного интеграла для решения прикладных задач.
- •1. Вычисление площадей плоских фигур.
- •Некоторые задачи экономики.
- •3.2.4.Приближенное вычисление определенного интеграла.
- •Контрольные вопросы.
- •Тест «Определенный интеграл. Площадь криволинейной трапеции».
- •Задания для самостоятельного решения.
- •Контрольное задание.
- •Основные понятия. Предел и непрерывность функции в точке.
- •Интеграл и его приложения.
- •Производные основных элементарных функций.
- •Интегралы от основных элементарных функций.
- •Литература.
3. 1. 2. Неопределенный интеграл.
Неопределенный интеграл функции - это совокупность всех первообразных функции для функции .
Обозначается
символом
![]() ,
где
,
где
![]() -знак
интеграла (это стилизованная латинская
буква
,
обозначающая
суммирование);
-
подынтегральная функция;
-знак
интеграла (это стилизованная латинская
буква
,
обозначающая
суммирование);
-
подынтегральная функция;
![]() -
подынтегральное выражение;
-
постоянная интегрирования, способная
принимать любое значение;
-переменная
интегрирования.
-
подынтегральное выражение;
-
постоянная интегрирования, способная
принимать любое значение;
-переменная
интегрирования.
Г еометрический
смысл неопределенного интеграла: это
семейство кривых, зависящих от одного
параметра
,
которые получаются путем параллельного
сдвига вдоль оси
.
еометрический
смысл неопределенного интеграла: это
семейство кривых, зависящих от одного
параметра
,
которые получаются путем параллельного
сдвига вдоль оси
.
Рисунок 13
3. 1. 3. Основные свойства неопределенного интеграла.
Производная неопределенного интеграла равна подынтегральной функции, т.е.
 .
.Постоянный множитель подынтегрального выражения можно вынести за знак интеграла, т.е.
 ,
где
,
где
 -
постоянная величина, не равная нулю.
-
постоянная величина, не равная нулю.Интеграл от алгебраической суммы функций равен алгебраической сумме интегралов от этих функций, т.е.
 .
.Дифференциал неопределенного интеграла равен подынтегрального выражения, т.е.
 .
.Неопределенный интеграл от дифференциала(производной) некоторой функции равен сумме этой функции и произвольной постоянной , т.е
 или
или

3. 1. 4. Основные способы интегрирования.
Метод непосредственного интегрирования, который заключается в использовании основных свойств неопределенного интеграла и приведении подынтегрального выражения к табличному виду.
Таблица основных формул интегрирования
1 |
|
10 |
|
2 |
|
11 |
|
3 |
|
12 |
|
4 |
|
13 |
|
5 |
|
14 |
|
6 |
|
15 |
|
7 |
|
16 |
|
8 |
|
|
|
9 |
|
Пример 30.
Найти неопределенный интеграл
![]()
Решение.
Используя
свойство неопределенного интеграла:
интеграл от суммы равен сумме интегралов,
и постоянный множитель можно выносить
за знак интеграла, а также формулы 3 и
6, получаем:
![]()
Пример 31.
Найти неопределенный интеграл
![]()
Решение.
![]()
2.Метод подстановки или введения новой переменной.
Это самый эффективный прием сведения неопределенного интеграла к табличному виду.
Способ подстановки заключается в следующем: заменяют новой переменной такую часть подынтегральной функции, при дифференцировании которой получается оставшаяся часть подынтегрального выражения (не считая постоянного множителя, на который всегда можно умножить и разделить подынтегральное выражение).
Правило интегрирования методом подстановки состоит в следующем: - Определяют, к какому табличному интегралу приводится данный интеграл (предварительно преобразовав подынтегральное выражение, если нужно). - Определяют, какую часть подынтегральной функции заменить новой переменной и записывают эту замену. - Находят дифференциалы обеих частей записи и выражают дифференциал старой переменной через дифференциал новой переменной. - Производят замену под интегралом. - Находят полученный интеграл. - В результате производят обратную замену, т.е. переходят к старой переменной. Результат полезно проверить дифференцированием.
Пример 32.
Найти неопределенный интеграл
![]()
Решение.
=![]() =
=![]() .
.
Пример 33.
Найти неопределенный интеграл
![]() .
.
Решение.
=![]() =
=![]()
Пример 34.
Найти неопределенный интеграл
![]() .
.
Решение.
=![]() =
= .
.
Правило.
Интеграл от нечетной степени синуса
или косинуса находим путем отделения
одного множителя, затем, используя
формулу
![]() ,
разбиваем на два интеграла, и далее
используем замену переменных.
,
разбиваем на два интеграла, и далее
используем замену переменных.
Пример 35.
Найти неопределенный интеграл
![]() .
.
Решение.
=![]()
![]()
Правило.
Интеграл от четной степени синуса или
косинуса можно найти путем понижения
степени вдвое по формуле половинного
аргумента:
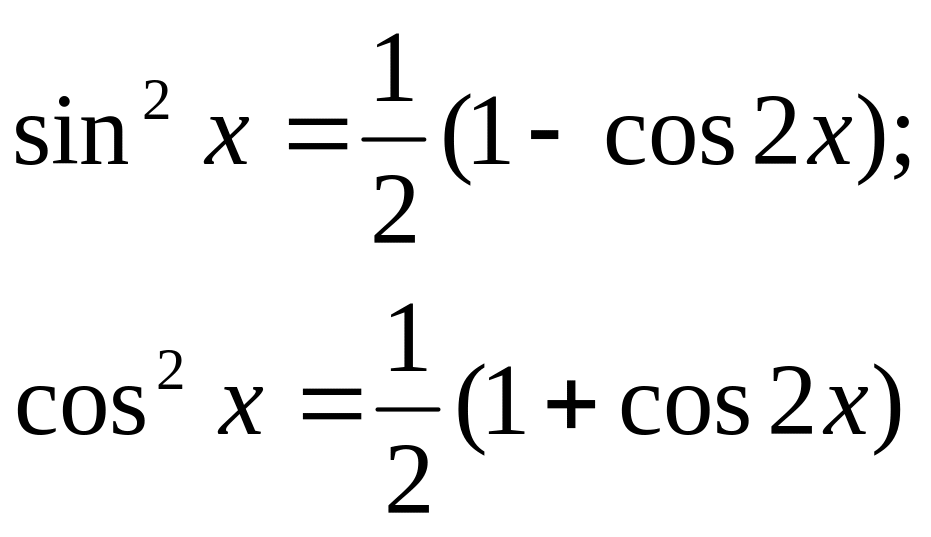
Пример 36.
Найти неопределенный интеграл
![]() .
.
Решение.
![]()