2.10.5. Схема исследования функции.

К данному моменту наших математических построений накопился довольно большой набор средств, которые могут использоваться при исследовании функциональных зависимостей. Поэтому полезно объединить их в определенный комплекс и представить в виде схемы, которая могла бы задавать общие ориентиры исследования. Например, так:

Исследование области определения функции. Это, пожалуй, единственная рекомендация, которой нужно настойчиво следовать в начале каждого исследования свойств функции. Нарушение ее существенно затрудняет анализ и может привести к ошибкам.
Выявление существенных классификационных свойств функции. Например, четности, нечетности, периодичности, если возможно, множества значений функции, ее ограниченности и неограниченности и т.д.
Выявление характерных точек. Полезно найти точки пересечения графика функции с осью ( положив ) и с осью - ( приравняв 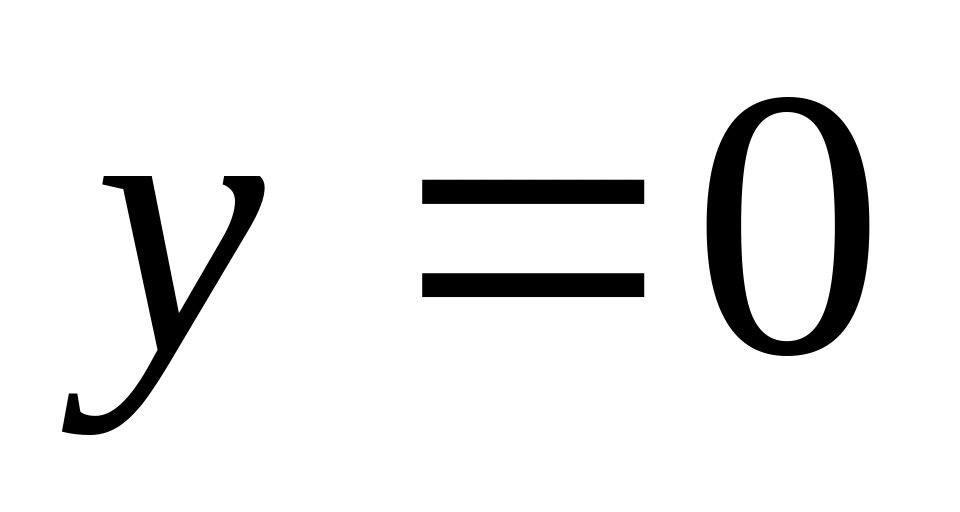); обозначить точки разрыва, границы области определения и исследовать поведение функции вблизи них; выявить точки в которых отсутствует производная, исследовать поведение функции в их окрестностях.
Нахождение стационарных точек. Решается уравнение .Для определения интервалов монотонности к стационарным точкам присоединяют точки, в которых не существует производная.
Исследование функции на монотонность. Оно сводится к определению знака производной на интервалах, которые обозначены на предыдущем этапе.
Исследование функции на экстремум. Для этого можно использовать достаточные условия. Экстремальные значения вычисляют и обозначают на графике. В случае если функция определена на отдельных отрезках, исследуются и значения функции на концах отрезков.
Исследование функции на выпуклость, вогнутость, точки перегиба. Вычисление второй производной полезно и при исследовании функции на экстремум. Если вторая производная имеет не очень сложный вид, то нахождение интервалов выпуклости и вогнутости, а также точке перегиба оказывается весьма эффективным средством изучения поведения функции.
Исследование асимптотического поведения функции. Речь идет не только о вертикальных, горизонтальных и наклонных асимптотах, но и о сравнении поведения данной функции с поведением других, более простых.
Уточнение графика функции по точкам. Все результаты исследования, полученные на предшествующих этапах, рекомендуется сразу же отмечать на графике. Поэтому график изучаемой функции вначале обычно выглядит как эскиз, постепенно уточняемый. На данном этапе производится окончательное уточнение графика, как правило, на участках, где информация о нем недостаточна.

Данную схему можно варьировать в зависимости от конкретных особенностей функции, переставлять отдельные этапы, некоторые из них опускать, какие-то, наоборот, добавлять. Если, же следуя схеме, предусмотреть обозначенное в ней содержание исследования, легко заметить, что отдельные этапы позволяют контролировать правильность рассуждений на других этапах и облегчают их осуществление.

Пример 28. Исследовать функцию и построить ее график .

Решение.

Область определения функции: .
Функция нечетная, т.к. . Следовательно, она симметрична относительно начала координат. Функция непериодическая.
Функция непрерывна и точек разрыва нет. Точки пересечения графика с осью : Пусть , тогда В этих трех точках график пересекает ось : Точки пересечения графика с осью : Пусть , тогда . Итак, график функции пересекает ось в точке
Найдем стационарные точки:

	-1		1
+	0	-	0	+
	2		-2
	max		min

Исследуем функцию на монотонность.

Исследуем функцию на экстремум. При переходе через точку производная меняет свой знак с плюса на минус, значит, - точка максимума. При переходе через точку производная меняет свой знак с минуса на плюс, значит, - точка минимума.

	0
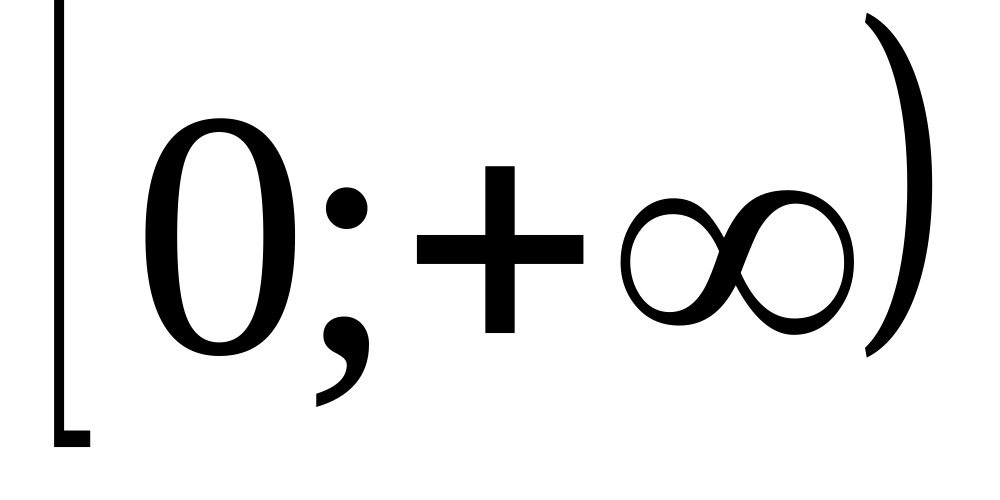
-	0	+
выпукла	0	Вогнута
	Точка перегиба

Исследуем функцию на выпуклость, вогнутость, точки перегиба.
Найдем вторую производную и решим уравнение

При переходе через точку вторая производная меняет знак: при , функция выпукла вверх. При функция выпукла вниз(вогнута). Следовательно, - точка перегиба.

Вертикальных асимптот нет, т.к. функция непрерывна. Наклонных асимптот также нет, т.к.
П остроим график функции.

Рисунок 11

Пример 29. Исследовать функцию и построить ее график.

Решение.

Область определения функции :
Функция нечетная, т.к. Следовательно, график функции симметричен относительно начала координат. Функция непериодическая.
Точки пересечения с осью . Решаем уравнение: , получаем 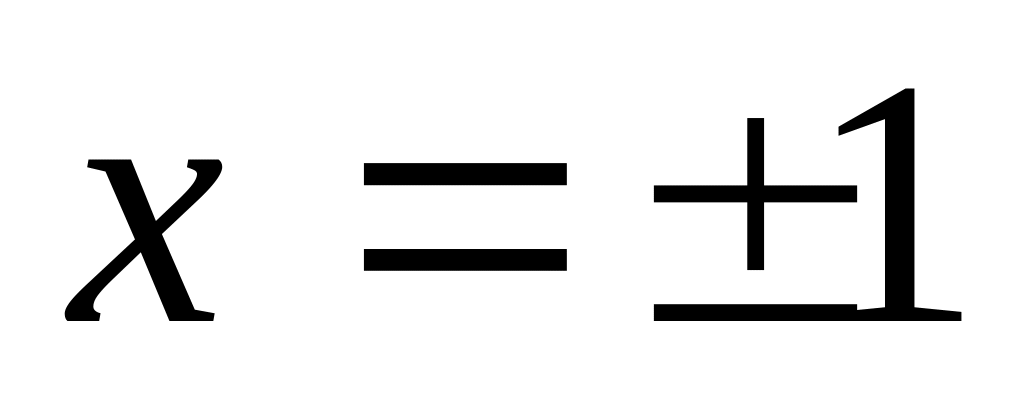.Точек пересечения с осью нет, т.к. .
Найдем стационарные точки. 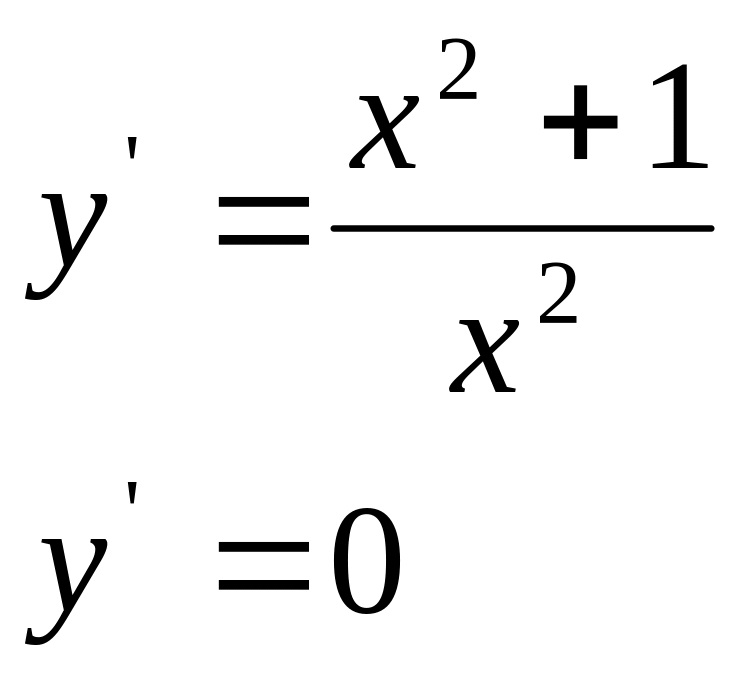Не существует точек, в которых производная равна нулю.
В области определения функции , значит, функция монотонно возрастает.
Исследуем функцию на выпуклость, вогнутость, точки перегиба. . В правой координатной полуплоскости выпуклость графика направлена вверх, т.к. . В левой полуплоскости – вниз, т.к. .
Вертикальная асимптота – ось , т.к. и . Уравнение наклонной асимптоты: Уравнение наклонной асимптоты
П остроим график функции.