IV.Пример решения контрольной работы

Задача I.1. Даны множества:

А = –1; 0; 1,

В = –2; 0) – полуинтервал на числовой оси,

С = –0.5; 2 - отрезок на числовой оси.

Н айти:

Изобразить на плоскости: А  В, А  С, В  С. Найти , считая универсальным множеством множество всех вещественных чисел.

Решение:

= –2; 0; 1

= –1; –0.5; 2

= –2; 2

= –2; 2

= –1

= 0; 1

= –0.5; 0)

=  – пустое множество

А \ В = 0; 1

В \ А = –2; –1); (–1; 0)

А \ С = –1

С \ А = –0.5; 0); (0; 1); (1; 2

B \ C = [–2; –0.5)

C \ B = [0; 2]

( A \ B) \ C = 

A \ (B \ C) = {0; 1}

Задача I.2. Доказать тождество, используя диаграммы Эйлера-Венна.

Р ешение: Изобразим диаграмму для левой части тождества по шагам:

Т еперь диаграмму правой части по шагам:

Ввиду того, что заштрихованные области, полученные на последнем шаге для левой и правой части тождества, одинаковы, можно заключить, что исходное выражение верно.

Задача II. 1. Даны множества А={a,b,c} и B={1,2,3,4} и два бинарных отношения: P₁={(a,1); (a,3); (b,2); (c,1); (c,4)} и P₂={(1,1); (1,3); (2,2); (2,1); (2,4); (3,3); (4,1); (4,4)}

Изобразить Р₁, Р₂ графически. Найти: Р₁^-1, Р₂^-1, . Определить, является ли отношение Р₂ рефлексивным, транзитивным, симметричным, антисимметричным.

Решение: рассмотрим два способа графического представления бинарных отношений:

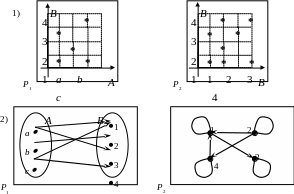
По определению обратное отношение . Таким образом, Р₁^-1={(1,a); (3,a); (2,b); (1,c); (4,c)} и P₂^-1={(1,1); (3,1); (2,2); (1,2); (4,2); (3,3); (4,4); (1,4)}.

По определению композиции бинарных отношений

Таким образом, ={(a,1); (a,3); (b,2); (b,1); (b,4); (c,1); (c,3); (c,4)}.

Тогда ^-1={(1,a); (3,a); (2,b); (1,b); (4,b); (1,c); (3,c); (4,c)}.

={(1,a); (1,c); (3,a); (3,c); (2,b); (1,b); (4,b); (4,c)}

Последние два множества совпадают, что и должно быть по свойствам композиции.

Отношение Р₂ рефлексивно, т. к. в соответствии с определением рефлексивности .

a)Отношение Р₂ не является транзитивным, поскольку по определению транзитивности требуется, чтобы для любых пар (x, y) и (y, z), таких что (x, y) следовало бы, чтобы пара . Однако это не так. Например, пары (2,1) и (1,3)  Р₂, но пара (2,3)  Р₂.

b)Отношение Р₂ не является симметричным, т. к. по определению симметричности для любой пары (x, y)  Р₂ должно быть и (y, x)  Р₂ . Однако это не так. Например, пара (1,3) Р₂ , но пара (3,1)  Р_2.

c)Отношение Р₂ антисимметрично, поскольку для любой пары (x, y)  Р₂ такой, что (y, x)  Р₂ обязательно следует, что x=y.

Задача II. 2

Даны две функции и и два отрезка A = [0; 3] и B = [ ‑1; 0]. Найти :f∘g, g∘f, f ^‑1, g ^‑1, (f∘g) ^‑1,(g∘f) ^‑1 ,f(A), g(A), f ^‑1(B), g^‑1(B). Найти неподвижные точки f и g.

Решение: по свойствам композиции находим

(f∘g)(x) = f(g(x)) = (g(x)–2)²–1 = (1–x–2)² –1 = (–x–1)² – 1=(x+1)²–1;

(g∘f)(x) = g(f(x)) =1– f(x) = 1 – (x–2)² +1 = 2 – (x–2)² ;

Т.к. , где y –1. То из выражения найдем x. Тогда , где y –1 и f ^‑1(у) – не является всюду определенным и однозначным соответствием.

Заметим, что исходное отображение f обратимо справа, а именно: :f∘f ^‑1 = f(f ^‑1(y))= – тождественное отображение при y ‑1.

Аналогично, , где y любое. И из следует: , при этом исходное отображение g обратимо как справа, так и слева, а именно: g∘g^‑1 = g(g^‑1(y)) = 1– (1– y)= y и g^‑1∘g = – тождественные отображения.

По свойствам композиции

f(A) = { y = f(x), где xA }, поэтому f(A)=[–1; 3].

Аналогично, g(A) = { y = g(x), где xA } = [–2; 1].

Найдем неподвижные точки. По определению это такие х, что: f(x)=x и g(x)=x. Таким образом, x = (x–2)²–1. Отсюда x²–5x+3=0 и т. к. дискриминант D=25–12=13>0, то – две неподвижные точки f(x).

Из g(x)=x следует, что x=1–x и – неподвижная точка g(x).

Задача III. 1.

Составить полную и сокращенную таблицы истинности для формул:

x	y	f1	f2	f3	f4
0	0	1	0	0	1
0	1	1	1	1	0
1	0	0	1	1	0
1	1	0	1	1	0

Решение:
для построения полной таблицы истинности первой формулы выделим подформулы: Таким образом, таблица будет содержать 4 строки и 6 столбцов.

Значения формулы совпадают со значениями последнего столбца таблицы.

Сокращенная таблица истинности строится непосредственно под формулой. Столбец результата выделяем. Стрелками показываем столбцы, участвующие в операции. Номером – столбец, полученный в результате операции.

( 	x		y)		(y		x)
1	0	0	0	1	0	0	0
1	0	1	1	0	1	1	0
0	1	1	0	0	0	1	1
0	1	1	1	0	1	1	1

Выделим подформулы второй заданной формулы:

Построим полную таблицу истинности.

x	y	z	f1	f2	f3	f4	f5	f6	f7
0	0	0	0	1	1	1	0	1	1
0	0	1	0	1	0	1	0	1	1
0	1	0	1	1	1	1	1	1	1
0	1	1	1	0	0	1	0	1	0
1	0	0	1	1	1	0	0	0	0
1	0	1	1	0	0	0	0	0	1
1	1	0	0	1	1	0	1	1	1
1	1	1	0	1	0	0	0	0	0

Сокращенная таблица истинности для 2-ой формулы:

( (x		y)	|	z)		(y	&			)
0	0	0	1	0	1	0	0	1	1	1
0	0	0	1	1	1	0	0	0	1	1
0	1	1	1	0	1	1	1	1	1	1
0	1	1	0	1	0	1	0	0	1	1
1	1	0	1	0	0	0	0	1	0	0
1	1	0	0	1	1	0	0	0	0	0
1	0	1	1	0	1	1	1	1	1	0
1	0	1	1	1	0	1	0	0	0	0

Заметим, что для обеих формул результаты, полученные в полной и сокращенной таблице истинности, совпали. Это подтверждает правильность вычислений.

Задача III. 2.

Проверить двумя способами, будут ли эквивалентны следующие формулы: . а) составлением таблиц истинности; б) эквивалентными преобразованиями.

Решение: а) составим сокращенные таблицы истинности обеих формул:

x		(y		z)	(x		y)		(x		z)
0	1	0	0	0	0	1	0	0	0	1	0
0	0	0	1	1	0	1	0	1	0	0	1
0	0	1	1	0	0	0	1	1	0	1	0
0	1	1	0	1	0	0	1	0	0	0	1
1	0	0	0	0	1	0	0	0	1	0	0
1	0	0	1	1	1	0	0	0	1	0	1
1	0	1	1	0	1	0	1	0	1	0	0
1	0	1	0	1	1	0	1	0	1	0	1

Поскольку полученные столбцы не совпадают, формулы не эквивалентны.

б) Выполним преобразования формул, перейдя к системе связок {, &, }. Для этого воспользуемся тождествами: и , где a и b – произвольные формулы. Тогда (по закону де Моргана) (по закону дистрибутивности)=

Формулы (*) и (**) не эквивалентны.