Для того, чтобы задать вектор, необходимо указать:

1) прямую, на которой лежит вектор или которой он параллелен;

2) направление (ориентацию) вектора на этой прямой;

3) длину вектора.

Один и тот же вектор может быть отложен от любой точки пространства при помощи параллельного переноса, при этом сохраняются все три указанные характеристики этого вектора.

• Вектор называется нулевым, если его начало и конец совпадают:

• Векторы называются коллинеарными, если они лежат на параллельных или совпадающих прямых, обозначают  .

• Векторы называются сонаправленными, если они коллинеарны и одинаково направлены.

• Векторы называются равными, если они сонаправлены и имеют одинаковую длину, обозначают .

Заметим, что от любой точки пространства можно отложить вектор , равный данному, и при этом только один.

• Три вектора называются компланарными, если они лежат в одной плоскости или в параллельных плоскостях.

5.2. Операции над векторами

• Суммой двух векторов называется вектор , построенный по правилу параллелограмма или треугольника:

Из правила треугольника сложения векторов следует правило их вычитания: действительно, если , то .

• Произведением вектора на число  называется вектор , коллинеарный вектору , длиной 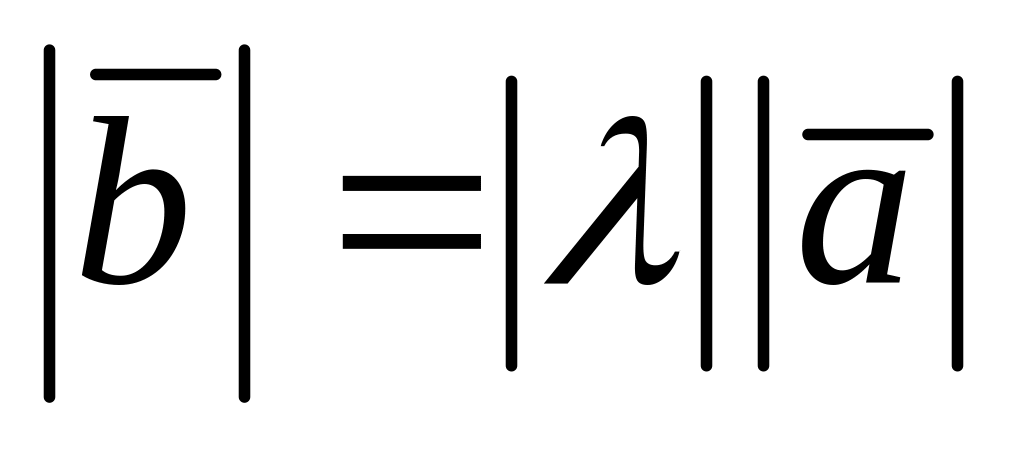, который сонаправлен с вектором , если >0 и противоположно направлен, если <0.

• Любому ненулевому вектору можно поставить в соответствие орт , имеющий единичную длину 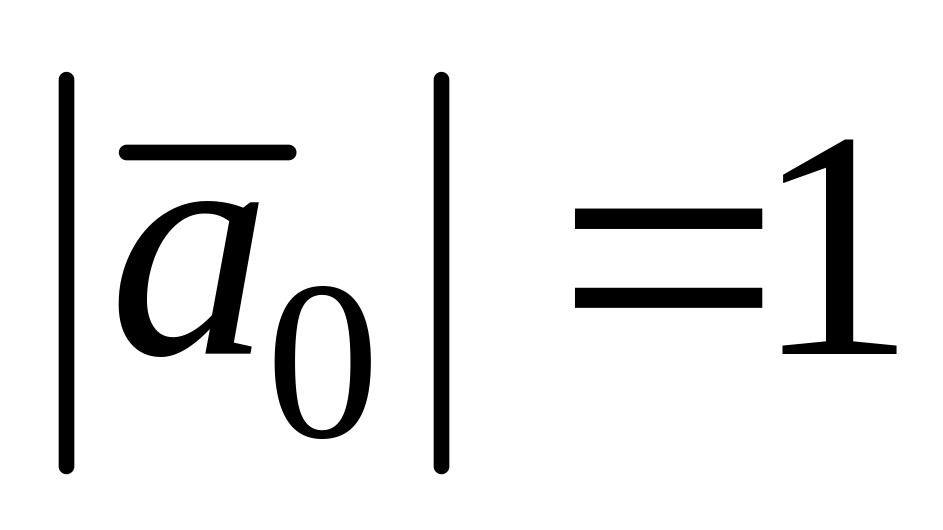и направление которого совпадает с направлением вектора .

Свойства:

1)

2)

3)

4)

5)

Теорема 5.1. Векторы коллинеарны тогда и только тогда, когда для некоторого .

Пример. В треугольнике АВС точки M, N, K – середины сторон АВ, АС, ВС соответственно. Найти векторы , если .

Р ешение: По условию, . Применяя правило вычитания, находим:

, .

Далее, AK - половина диагонали параллелограмма, сторонами которого являются отрезки АВ и АС (так как диагонали параллелограмма точкой пересечения делятся пополам). Следовательно, по правилу параллелограмма сложения векторов, имеем .

5 .3. Координаты векторов

Рассмотрим трехмерное пространство.

• О

  y

  y

  ртонормированным репером в трехмерном пространстве называется совокупность начальной точки О и векторов , таких, что:

1) (единичные векторы),

2) (попарно перпендикулярные),

3) векторы образуют правую тройку векторов, то есть из конца вектора поворот от вектора к вектору виден в положительном направлении – против часовой стрелки.

В таком случае обычная декартова система координат соответствует заданному ортонормированному реперу, так что направления осей Ох, Оу, Oz совпадают с направлениями базисных векторов .

Р ассмотрим теперь произвольный вектор в трехмерном пространстве.

• Координатами вектора называются его проекции а₁, а₂, а₃ на оси координат. Обозначают: .

Отметим, что если вектор отложен от начала координат, то его координаты совпадают с координатами конца этого вектора.

Применив дважды правило параллелограмма, замечаем, что

.

• Это соотношение называется разложением вектора по базису .

Свойства:

Пусть , . Тогда

1)

2)

3)

4 )

Теорема 5.2. Пусть точка А имеет координаты (x_A, y_A, z_A), точка В(x_В, y_В, z_В). Тогда

.

Для доказательства достаточно заметить, что , причем .

Замечание. Координаты вектора не изменятся, если этот вектор отложить от любой другой точки пространства.

Доказательство этого факта предоставим читателю.

Многие геометрические задачи на плоскости и в пространстве легко решаются с помощью векторов. При этом надо все условия задачи, сформулированные для точек и отрезков (а в дальнейшем – и углов) переформулировать для векторов, а затем перевести в координатную форму. Если рассматривается задача на плоскости, то и точки, и векторы имеют 2 координаты, и все сформулированные выше свойства имеют место для первых двух координат.

Пример 1: Точка М делит пополам отрезок АВ, где А(x_A, y_A, z_A),

В(x_В, y_В, z_В). Найти координаты точки М.

Решение: Для решения этой задачи используем векторы.

Точка М лежит на отрезке АВ   , причем эти векторы сонаправлены.

Кроме того, по условию, . Следовательно, .

Обозначим координаты точки М (x_М, y_М, z_М). Тогда , .

Используя свойство 2) координат, имеем:

, откуда выражаем

.

Пример 2. Даны точки: A(1; 0), B(4; 2), C(2; 5). Найти точку пересечения медиан треугольника АВС.

Р ешение: Как известно, все медианы треугольника пересекаются в одной точке. Обозначим эту искомую точку К(x_K, y_K) и рассмотрим две медианы: BN и CM.

Найдем сначала координаты точек N и M как середин сторон АВ и АС (см. Пример 1).

Точка М – середина отрезка АВ  . Аналогично, .

Следовательно, можем найти координаты векторов:

Точка КСМ    (свойство 4). Аналогично,

точка КBN    .

Таким образом, мы получили два линейных уравнения с двумя неизвестными – координатами точки К. Решаем полученную систему:

 .

Таким образом, искомая точка .