4.8.5. Вейвлет-преобразования()

Как и в случае преобразований Фурье, возможны два вида вейвлет-преобразований - прямое и обратное. Прямое означает вейвлет-декомпозицию сигнала, т.е. его разложение по базису вейвлетов. В основе непрерывного вейвлет-преобразования НВП (или CWT — Continue Wavelet Transform) лежит использование двух непрерывных и интегрируемых по всей оси t (или x) функций:

• вейвлет-функция psi с нулевым значением интеграла ( ), определяющая детали сигнала и порождающая детализирующие коэффициенты;

• масштабирующая или скейлинг-функция phi 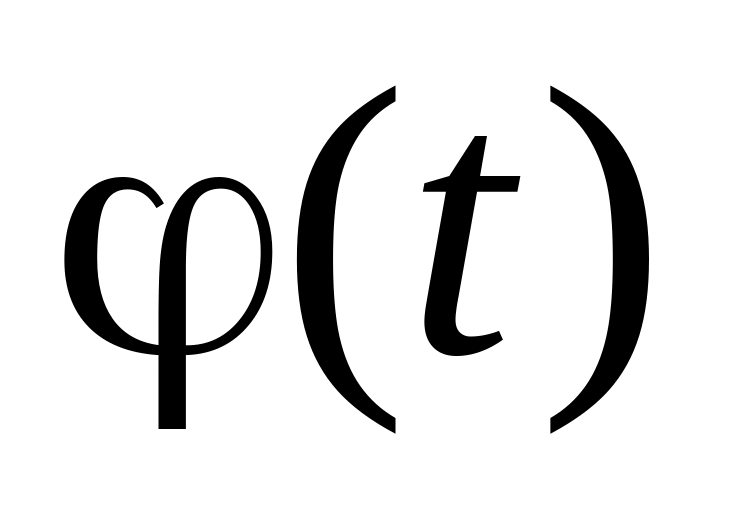с единичным значением интеграла ( ), определяющая грубое приближение (аппроксимацию) сигнала и порождающая коэффициенты аппроксимации.

Phi-функции присущи только тем вейвлетам , которые относятся к ортогональным. Psi-функция создается на основе той или иной базисной функции , которая, как и , определяет тип вейвлета. Базисная функция должна удовлетворять всем тем требованиям, которые были отмечены для psi-функции . Она должна обеспечивать выполнение двух основных операций:

• смещение по оси времени t  — при bR;

• масштабирование — при и aR⁺-{0}.

Параметр a задает ширину этого пакета, а b – его положение, R - задает область определения параметров, в общем случае бесконечную (верхний индекс + означает область положительную, а обозначение -{0} исключение нулевой точки). В ряде литературных источников вместо явного указания времени t используется аргумент x, а вместо параметров a и b используются имеющие тот же смысл иные обозначения. Нетрудно убедиться в том, что следующее выражение задает сразу два этих свойства функции :

.

Итак, для заданных a и b функция и есть вейвлет. Вейвлеты являются вещественными функциями времени t и колеблются вокруг оси t (или x). Параметр b задает положение вейвлетов, а параметр a — их масштаб. О вейвлетах, четко локализованных в пространстве (или во времени), говорят, что они имеют компактный носитель.

Прямое непрерывное вейвлет-преобразование (ПНВП) сигнала s(t) задается, по формальной аналогии с преобразованием Фурье, путем вычисления вейвлет-коэффициентов по формуле:

.

Если сигнал ограничен во времени a,bR, a0, то интегрировать можно в конечных пределах:

.

Обратное вейвлет-преобразование задается выражением

и обеспечивает восстановление сигнала.

Как уже отмечалось, на практике непрерывное изменение параметров a и b вызывает избыточность вейвлет-представления сигналов. Поэтому, как это описывалось в примере с вейвлетом Хаара, используется кратномасштабный (в частности диадический) метод.

К счастью, большинству пользователей системой Mathcad нет особой необходимости залезать в математические дебри вейвлет-преобразований. В системы Mathcad 2000/2001 включены две простые функции дискретных волновых преобразований:

• wave(V) — дискретное волновое преобразование действительных чисел с использованием 4-коэффициентного волнового базиса Добеши. Вектор V должен содержать 2ⁿ действительных значений, где n — целое число;

• iwave(V) — обратное преобразование относительно преобразования wave (V — вектор с числом элементов 2ⁿ).

Эти функции реализуют пирамидальный алгоритм быстрого вейвлет-преобразования.