4.8.3. Улучшенное спектральное моделирование дискретных сигналов()
Для ускорения вычисления коэффициентов Фурье дискретных, т. е. представленных своими отсчетами, сигналов широко используется простой метод прямоугольников. Если сигнал представлен только своими равномерно распределенными отсчетами, то такой метод является единственным научно обоснованным методом, обеспечивающим минимальную среднеквадратическую ошибку приближения. Однако, в соответствии с теоремой Котельникова, максимальное число гармоник в спектре сигнала равно половине числа отсчетов. Ограничение числа гармоник служит причиной возникновения эффекта Гиббса (сильные колебания в особых точках сигналов).
К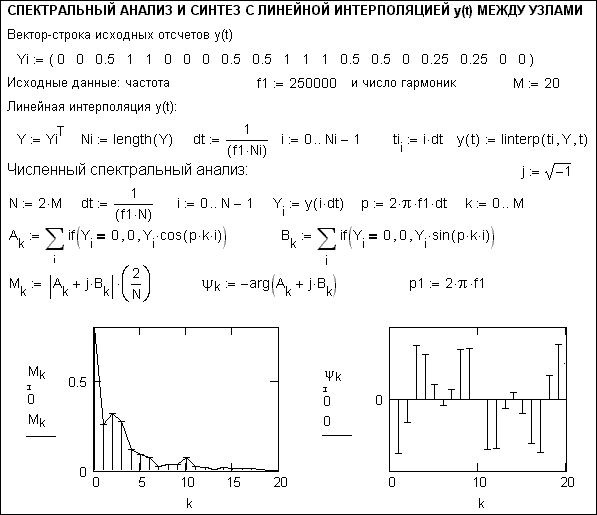
ардинальное
улучшение моделирования сигналов при
спектральном методе достигается заменой
дискретных отсчетов функции на плавную
функцию y(t),
получаемую при той или иной методике
интерполяции - рис.4.36. При этом появляется
возможность задавать произвольное
число отсчетов по интерполируемой
функции y(t)
и получить
сколь угодно большое число гармоник
для ее синтеза.
Рис. 4.36. Улучшенный спектральный анализ с прямой линейной интерполяцией функции между узлами (начало документа)
Этот прием дает блестящие результаты — при достаточно большом числе выбранных для синтеза гармоник синтезируемая функция почти повторяет исходную, а эффект Гиббса исчезает практически полностью.
Как видно из второй части документа (рис. 4.37), степень совпадения исходной и синтезируемой функций очень высока даже при числе используемых гармоник M=20. Это свидетельствует о высокой степени достоверности моделирования сложного сигнала на основе описанного подхода. При необходимости в формулы синтеза сигнала можно ввести поправочные множители, учитывающие искажения сигнала теми или иными устройствами, и обеспечить полную реализацию спектрального моделирования. Пример такого искажения, характерного для усилителя с верхней граничной частотой в 2 МГц также дан на рис. 4.37 (вторая формула синтеза). Нетрудно заметить, что искажения сигнала в этом случае заметно возросли.
Р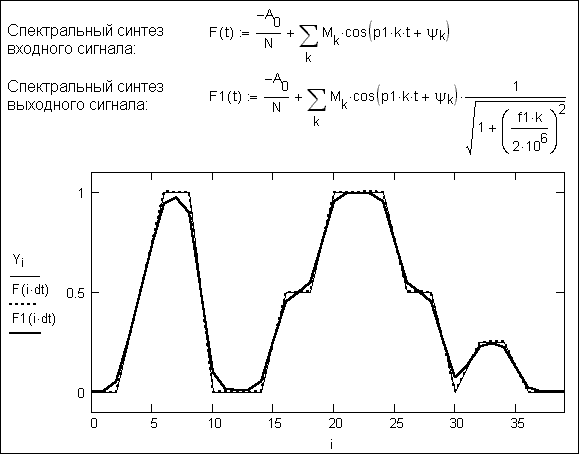
ис.
4.37. Улучшенный
спектральный анализ с прямой линейной
интерполяцией функции между узлами
(конец документа)
Описанная методика спектрального анализа наглядна и дает хорошие результаты при небольшом числе используемых гармоник - порядка десятков, иногда сотен. Однако реальные сигналы нередко бывают представлены многими тысячами отсчетов. В этом случае время спектрального моделирования при использовании прямых или упрощенных формул интегрирования становится недопустимо большим. Это оправдывает применение аппарата быстрого преобразования Фурье - БПФ или FFT. Более того, имеются специальные сигнальные процессоры для обработки сигналов, в которых БПФ реализуется на аппаратном уровне.
4.8.4. Вейвлеты - новый базис представления сигналов()
Из теории сигналов известно, что произвольный сигнал s(t) можно представить в виде взвешенной суммы простых составляющих — базисных функций k(t), помноженных на коэффициенты Ck:
(4.7)
Так как базисные функции k(t) предполагаются заданными как функции вполне определенного вида, то только коэффициенты Ck содержат информацию о конкретном сигнале. Таким образом, можно говорить о возможности представления произвольных сигналов на основе рядов общего вида (4.7) с различными базисными функциями. Так, хорошо известные синусоидальные функции легли в основу рядов Фурье, рассмотренных выше.С
Синусоиды-гармоники периодических сигналов (иные мы простоты ради не рассматриваем) предельно локализованы в частотной области, вырождаясь на спектрограммах в вертикальные линии, но не локализованы вообще во временной области - они определены в интервале времен - до +. Подобное определение является теоретической абстракцией. Поэтому содержащие их ряды Фурье плохо пригодны для представления коротких локальных особенностей сигналов и функций, таких, как перепады и скачки. В таких местах зарождается эффект Гиббса.
Более того, ряды Фурье в классическом виде принципиально непригодны для представления нестационарных сигналов. Представьте мысленно, что некоторый сигнал содержит N синусоидальных компонент с кратными частотами, действующими все время. А другой сигнал содержит эти компоненты, но действующие поодиночке на отрезках времени T/N, где T - период первой компоненты. Такие два сигнала имеют совершенно разную форму временной зависимости, но спектр Фурье их качественно абсолютно идентичен - это N линий с частотами компонент.
В связи с этим многие годы ученые искали иные базисы для разложения сигналов. В начале 90-х годов было обнаружено, что такие достаточно универсальные базисы и впрямь существуют и получили название вейвлетов. Термин вейвлет в переводе с английского wavelet означает «короткая или маленькая волна» или «волночка». На основе совокупности таких волн, перемещаемых и масштабируемых, и зародилась техника вейвлет-преобразований.
Оказалось, что простейший вейвлет Хаара (однократная волна прямоугольной формы в виде меандра ) был известен еще в 1910 г., но тогда никто не догадывался, что он является новым базисом декомпозиции произвольных функций и сигналов с возможностью их абсолютно точного восстановления. Затем были открыты десятки новых и старых вейвлет-функций, причем реализация большинства из них возможна только итерационными и программными методами.
Дадим наглядную трактовку применения вейвлетов Хаара [20]. Пусть имеется сигнал, представленный целочисленными компонентами вектора [9 7 3 5]. Это могут быть, например, значения пикселей некоторой подстроки изображения. Разрешение в этом случае равно 4. Перейдем к более грубому (вдвое меньшему) разрешению 2, для чего вычислим среднее из каждой пары компонентов сигнала. Получим вектор [8 4] с двумя детализирующими коэффициентами [1 -1]. Они представляют половину от приращений уровня относительно среднего значения, т.е. (9-7)/2=1 и (3-5)/2=-1.
Прибавив и отняв первый коэффициент от первого компонента вектора огрубленного сигнала - числа 8, получим компоненты 9 и 7. Аналогично, прибавив и отняв -1 от второго компонента вектора огрубленного сигнала 4, получим 3 и 5, т.е. вторую пару компонентов исходного вектора.
Продолжим огрублять сигнал вдвое и перейдем к разрешению 1. Наш вектор превратится в [6] с детализирующим коэффициентом 2. Его прибавление и отнимание дадут вектор [8 4]. Итак, для декомпозиции (разложения) исходного сигнала имеем:
Разрешение Аппроксимирующие Детализирующие
коэффициенты коэффициенты
4 [9 7 3 5]
2 [8 4] [1 -1]
1 [6] [2]
Таким образом, для представления сигнала достаточно хранить его грубое значение 6 и детализирующие коэффициенты 2, 1 и -1. Операции с ними задаются видом вейвлета Хаара. Например, на уровне разрешения 1 он представляется двумя функциями - аппроксимирующей с уровнем 1 и детализирующей с уровнем +1 на первой половине периода и -1 на второй половине периода (именно это задает вначале сложение, а затем вычитание детализирующего коэффициента). В итоге, осуществляя композицию сигнала, мы точно восстанавливаем его значение, используя последний (самый грубый) аппроксимирующий коэффициент и ряд детализирующих коэффициентов.
Процедуры изменения разрешения вдвое в ходе композиции и декомпозиции реализуют так называемый диадический метод. Он является разновидностью более общего кратномасштабного метода и лежит в основе устранения избыточности, свойственной непрерывным вейвлет-преобразованиям (см. ниже).
Казалось бы, какой прок в таком представлении, если число компонентов вектора осталось неизменным? Оказывается, прок есть, и весьма существенный. Прежде всего мы перешли от представления независимых значений сигнала к его приращениям. Коэффициенты вейвлет-представления реальных сигналов часто существенно меньшие числа, чем представления отсчетов сигналов. Для реальных сигналов многие коэффициенты по уровню оказываются настолько малыми, что их можно отбросить. Это означает возможность значительного сокращения объема информации о сигнале, выполнение его компрессии и очистки от шумов. Добавьте к этому, что сейчас есть множество куда более ценных и интересных вейвлетов, что дает обширный выбор базисных функций как для точного, так и приближенного представления любых сигналов.
Правда, точное представление могут давать только так называемые ортогональные вейвлеты. Объем этого раздела не позволяет остановиться на строгом определении ортогональности, как и многих иных свойств вейвлетов. Они даны в литературе по ним [7, 16, 19, 20]. Мы же будем исходить из того, что такие вейвлеты есть. Кроме вейвлета Хаара, к ним относятся хорошо известные вейвлеты Добеши, для прямого и обратного преобразований которых Mathcad имеет встроенные в ядро функции.