2. Определение основных метрик Холстеда
В MS Excel составить таблицу, содержащую все простые операторы выбранной программы и число вхождений каждого из них а программу. Вычислить число простых операторов, и общее число всех операторов. Аналогично составить таблицу, содержащую все простые операнды программы и число вхождений каждого из них а программу. Вычислить число простых операндов, и общее число всех операндов.
Составить формулы для вычисления и рассчитать следующие метрические характеристики (по Холстеду):
длину программы;
реальный и потенциальный объем программы;
теоретическую длину программы.
3. Определение дополнительных метрик Холстеда
В соответствии с кодом индивидуального задания составить формулы для вычисления и рассчитать дополнительные метрики.
Варианты заданий:
1. Уровень качества программирования, интеллектуальное содержание, трудоемкость понимания готовой программы, время программирования.
2. Оценка уровня качества программирования, интеллектуальное содержание, трудоемкость кодирования, уровень используемого языка программирования, ожидаемое число ошибок в программе.
3. Интеллектуальное содержание, время программирования, трудоемкость кодирования, ожидаемое число ошибок в программе.
4. Интеллектуальное содержание, уровень используемого языка программирования, ожидаемое число ошибок в программе.
5. Оценка уровня качества программирования, интеллектуальное содержание, трудоемкость понимания готовой программы, время программирования, ожидаемое число ошибок в программе.
6. Уровень качества программирования, интеллектуальное содержание, время программирования, ожидаемое число ошибок в программе.
7. Интеллектуальное содержание, трудоемкость кодирования, трудоемкость понимания готовой программы, ожидаемое число ошибок в программе.
8. Уровень качества программирования, интеллектуальное содержание, время программирования, уровень используемого языка программирования, ожидаемое число ошибок в программе.
9. Оценка уровня качества программирования, интеллектуальное содержание, трудоемкость кодирования, трудоемкость понимания готовой программы, ожидаемое число ошибок в программе.
10. Оценка уровня качества программирования, интеллектуальное содержание, трудоемкость кодирования, время программирования, уровень используемого языка программирования, ожидаемое число ошибок в программе.
Получить информацию об интеллектуальном содержании и ожидаемом числе ошибок в программах 5 других студентов группы, вычислить средние, минимальные и максимальные значения, построить диаграмму.
4. Топологические меры сложности
Оценки сложности программ по Холстеду к сожалению, не учитывают всех характеристик сложности программы. Программы со сложной графовой структурой и линейная, имеющие равный объем, обладают одинаковой сложностью, что в общем случае неверно. Топологические меры основаны на анализе структуры управления программы, представленной в виде управляющего графа или какой-либо другой графовой модели.
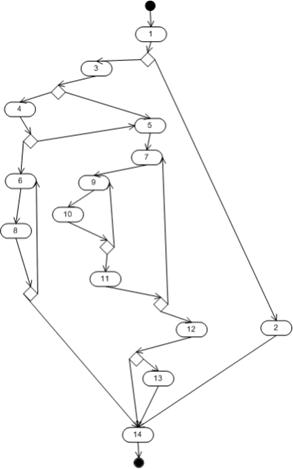
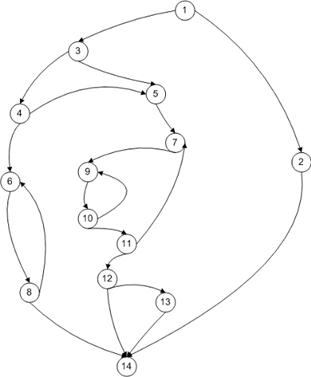
Управляющий граф - это ориентированный граф G=(V,E), где V – множество вершин, соответствующих операторам программы, а E - множество дуг, соответствующих возможным переходам в процессе выполнения программы от одного оператора к другому. Ниже приведены диаграмма действий некоторой программы и построенный по ней управляющий граф.
Диаграмма действий |
Управляющий граф |
