Vychmat_lektsii / Лекция 7 Собственные числа и векторы

11

Лекция 7 21.03.2007

Собственные числа и собственные вектора матриц.

Определение :

Рассмотрим квадратную матрицу А m-го порядка и m-го мерный вектор-столбец X , т.е.

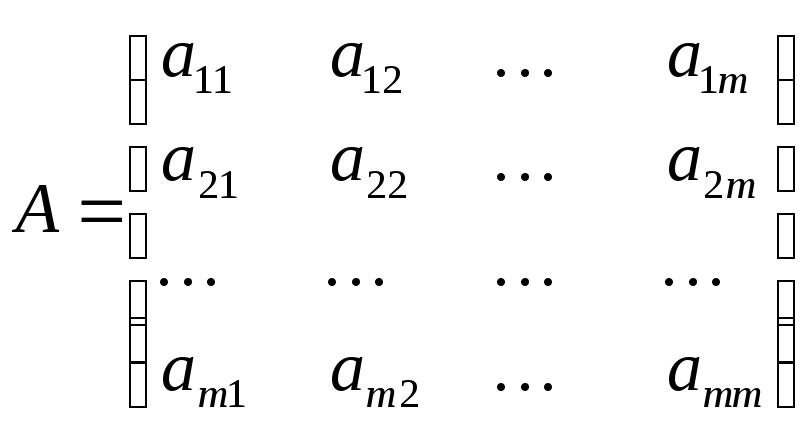
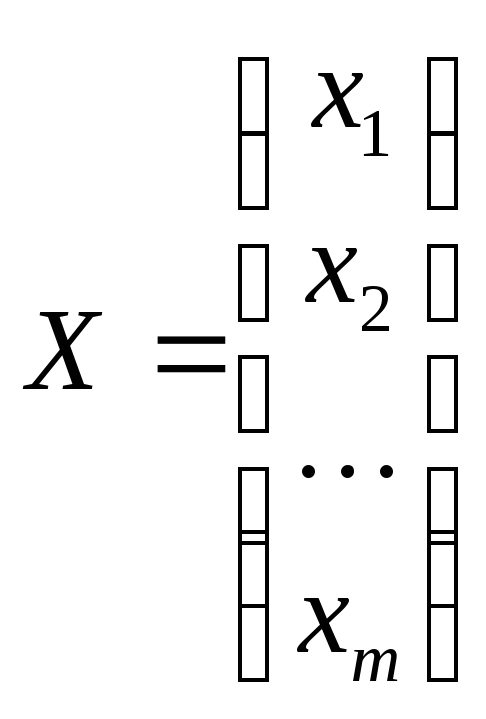
При исследовании структуры матриц большую роль играют такие векторы , при которых

, где  - число.

Если  и ненулевой вектор X удовлетворяют этому уравнению , то  называется собственным числом или собственным значением матрицы А , а Х – собственным вектором матрицы А , отвечающим  .

Замечание: Собственный вектор не может быть нулевым.

Вопрос : Сколько собственных чисел и какие их характеристики ?

Перепишем уравнение в виде:

Матрица

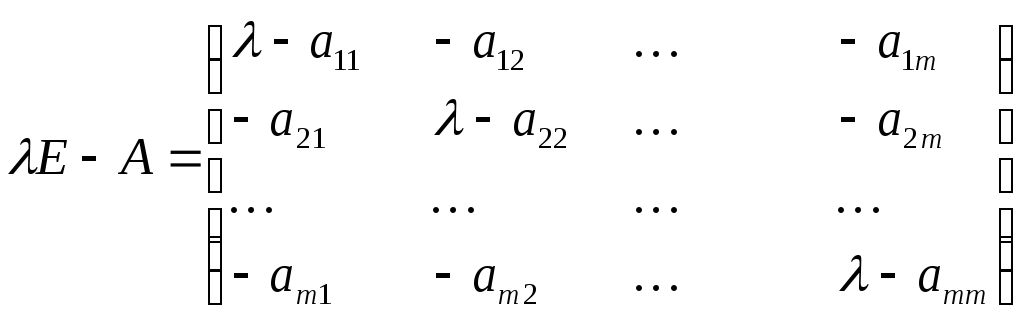называется характеристической.

Тогда матричное уравнение может быть записано так

Одна из координат собственного вектора должна быть отлична от нуля.

Для того , чтобы система линейных однородных уравнений имела ненулевое ( нетривиальное) решение , необходимо и достаточно , чтобы определитель этой системы был равен нулю, т.е.

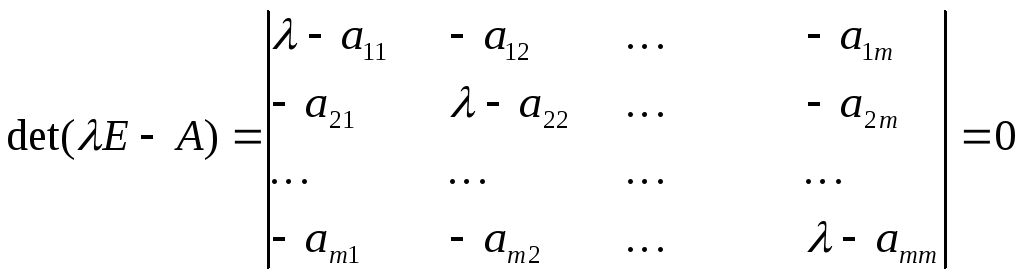
Таким образом , число _k будет собственным , если соответствующая характеристическая матрица будет вырожденной.

Уравнение det(E-A)=0 называется характеристическим уравнением матрицы А.

Это по сути есть алгебраическое уравнение относительно  степени m .

Понятно , что здесь имеется m корней.

Определение: Множество всех корней характеристического уравнения называется спектром матрицы А.

Среди корней могут оказаться и совпадающие между собой.

Каждому собственному значению спектра ставится в соответствие собственный вектор, определенный с точностью до скалярного множителя.

Пример:

Найти собственные числа и собственные вектора матрицы

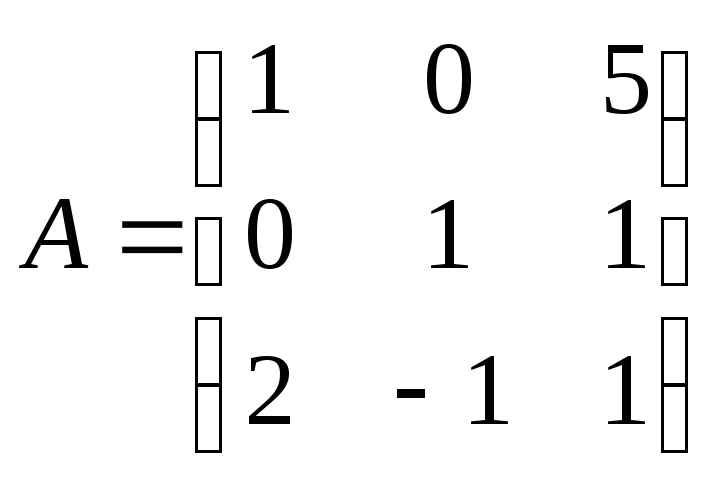имеем

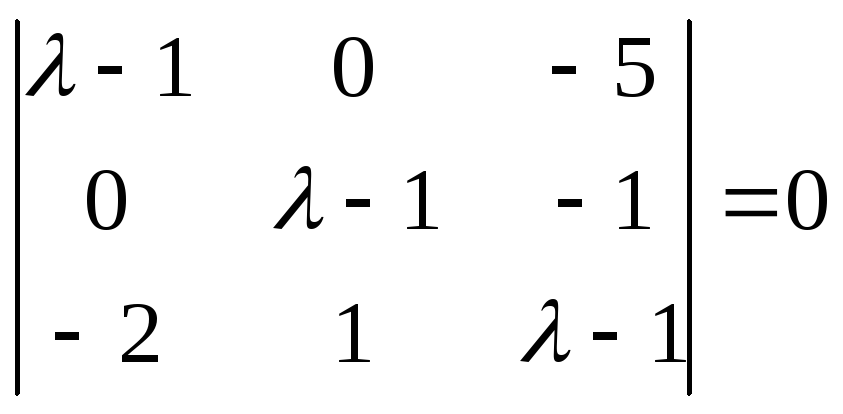
Характеристический полином имеет вид:

или

Собственные числа ₁=-2 , ₂=1, ₃=4

Согласно определению , собственные вектора будут такие:

₁=-2

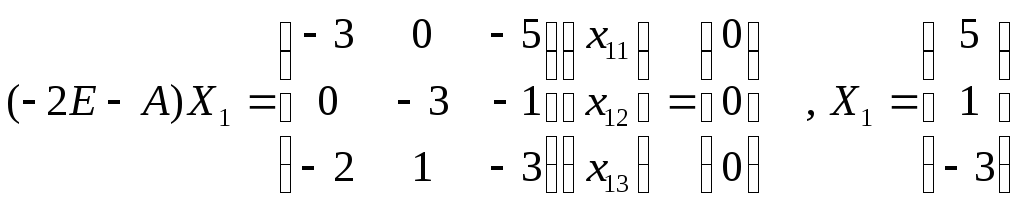
₂=1

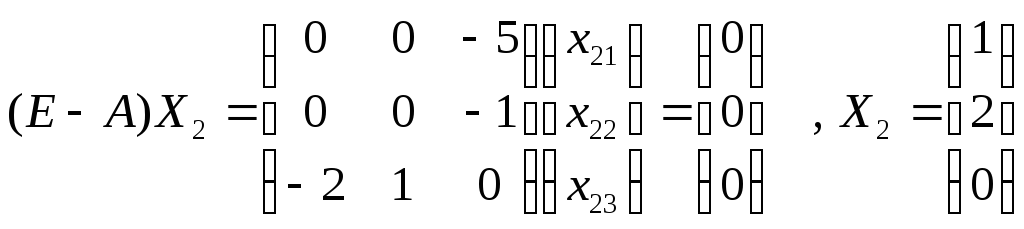
₃=4

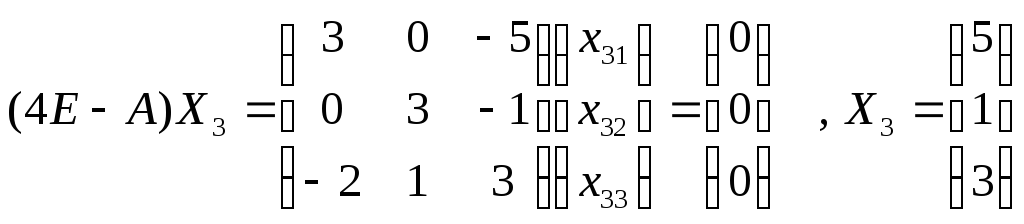
Надо заметить , что не всегда так просто решить характеристическое уравнение .

Задача нахождения собственных чисел и собственных векторов в общем случае сложнее чем решение СЛАУ методом итераций. Общего алгоритма решения характеристического полинома нет.

Однако! Если матрица А треугольная ( может быть верхней треугольной , нижней треугольной или диагональной) , то собственные числа в точности совпадают с диагональными элементами.

Пример 1.

Найти собственные числа и собственные вектора матрицы

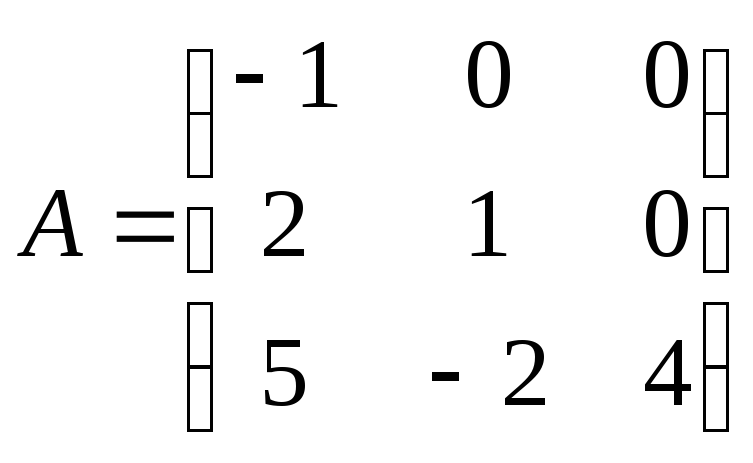имеем

Характеристический полином имеет вид:

Собственные числа ₁=-1 , ₂=1, ₃=4

Согласно определению , собственные вектора будут такие:

₁=-1

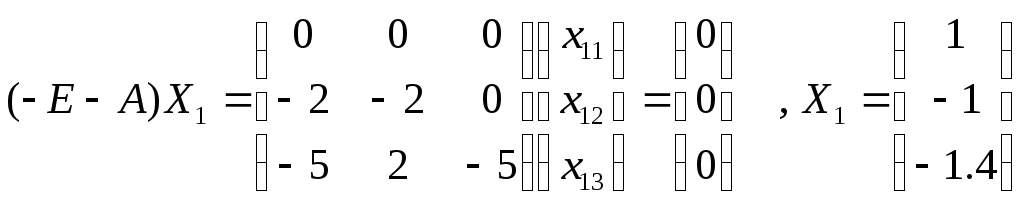
₂=1

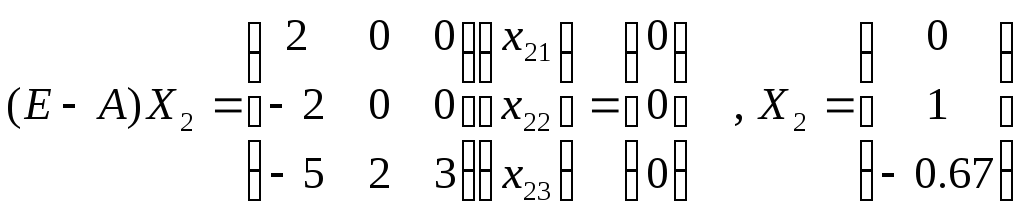
₃=4

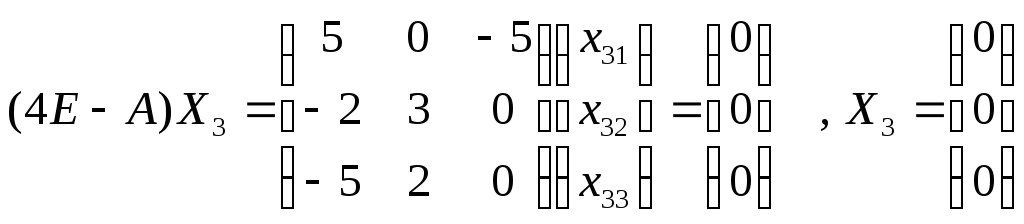
Более простой пример

Найти собственные числа и собственные вектора матрицы

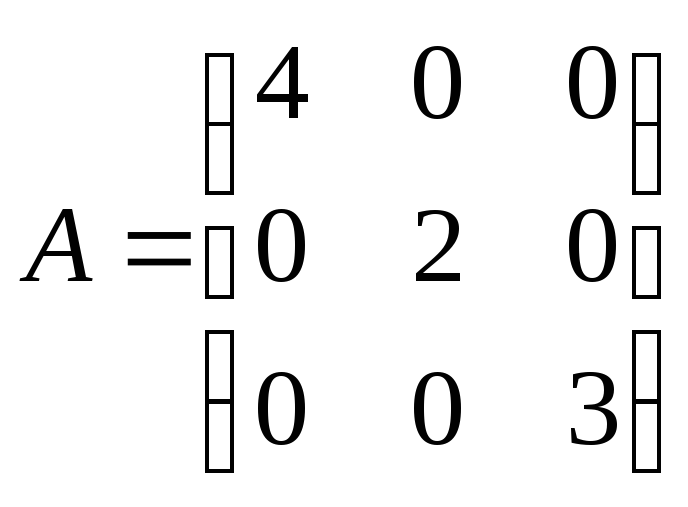имеем

Характеристический полином имеет вид:

Собственные числа ₁=4, ₂=2, ₃=3

Согласно определению , собственные вектора будут такие:

₃=4

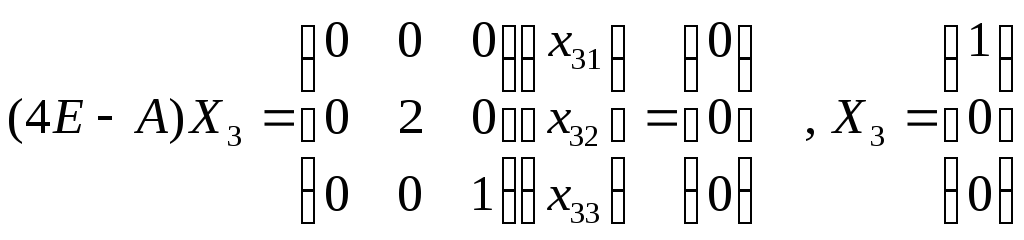
₁=2

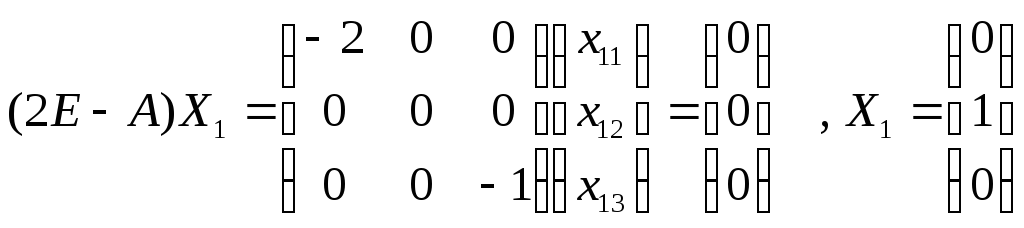
₂=3

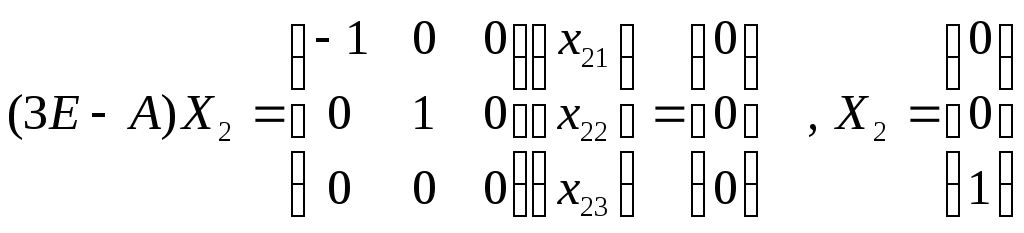
Можно записать проще

Тогда

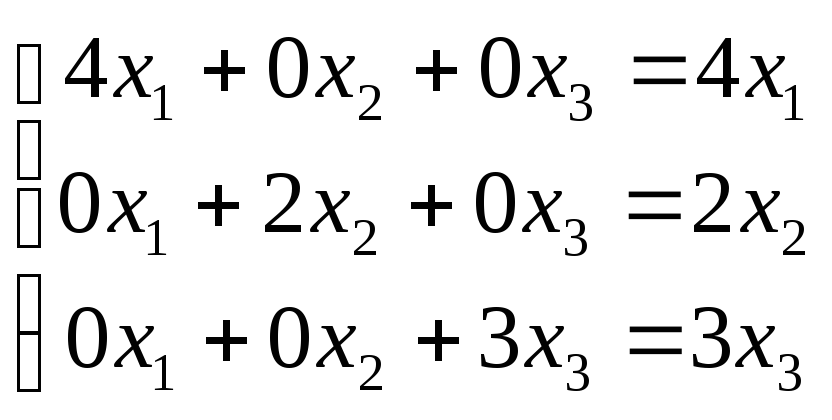
Два теста для вычисления собственных чисел:

1.Сумма m собственных чисел матрицы А равняется следу матрицы, т.е.

₁+₂+…+_m=a₁₁+a₂₂+…+a_mm

2. Произведение m собственных чисел матрицы А равно определителю матрицы А

₁₂…_m=detA

Локализация собственных значений

Иногда удается получить грубые оценки расположения собственных чисел.

Рассмотрим величину 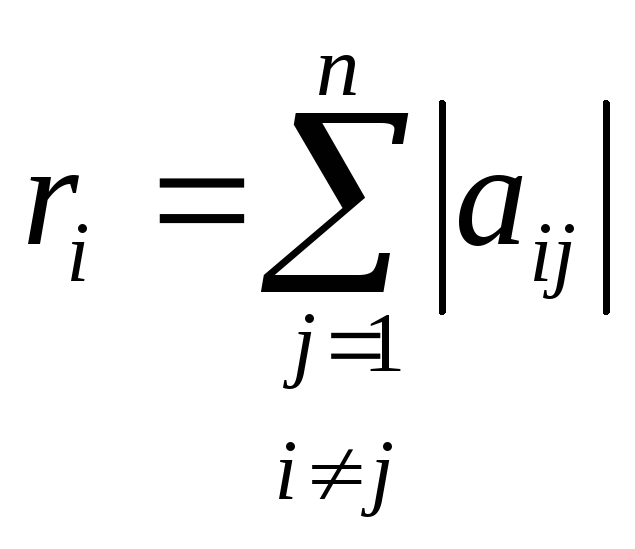- сумма внедиагональных элементов i-той строки матрицы А. Это некие радиусы кругов S_i на комплексной плоскости с центрами в точках соответствующих диагональных элементов a_ii и называются они кругами Гершгорина .

Теорема Гершгорина:

Все собственные числа матрицы А лежат в объединении кругов Гершгорина S₁,S₂…….S_n.если какой либо круг изолирован , то он содержит ровно одно собственное значение матрицы А.

Уравнение (А-λЕ)х=0 в скалярной форме

- максимальная по модулю координата вектора x.

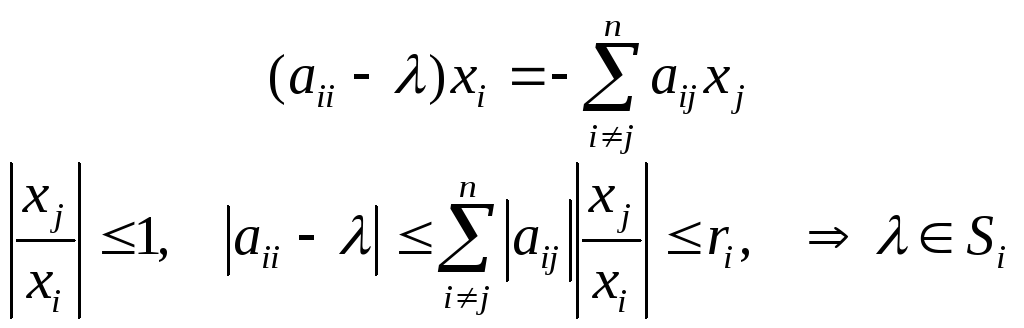
Пример :

Найти все собственные числа матрицы 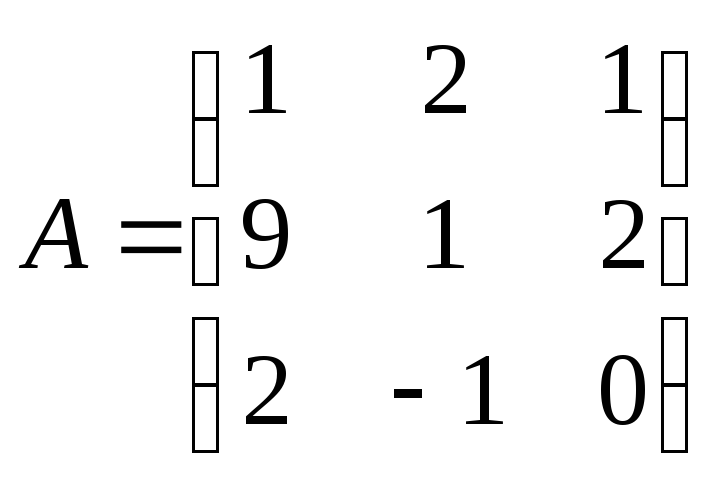и изобразить на плоскости круги Гершгорина.

Радиусы кругов

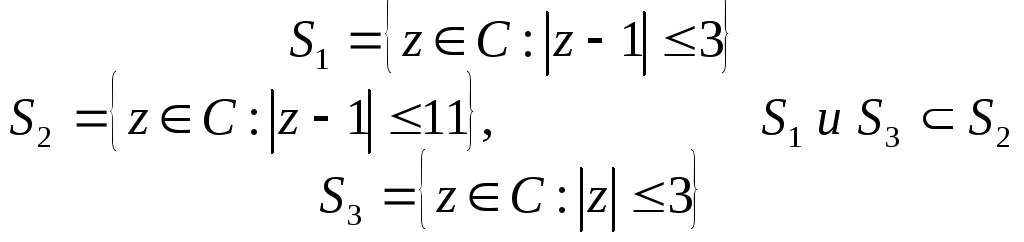
Составим характеристическое уравнение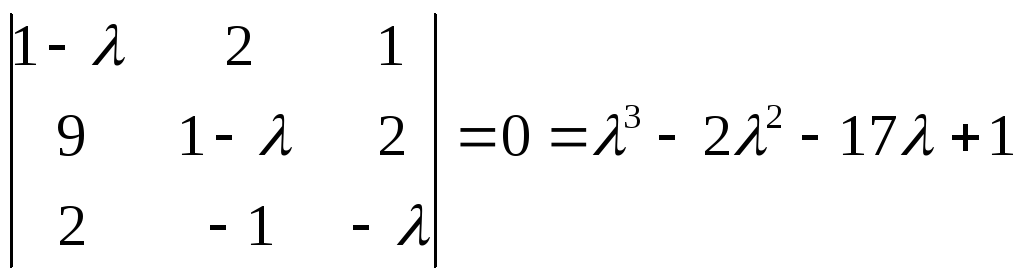

Произведем замену переменной: , тогда имеем:

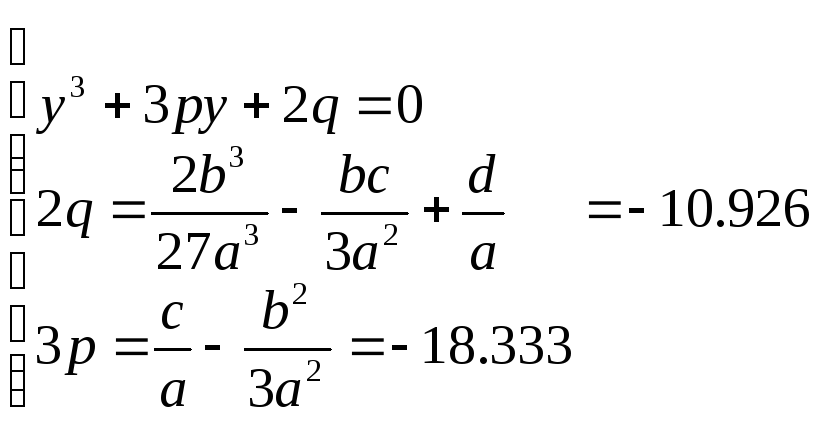
Число действительных корней зависит от знака дискриминанта D=q²+p³

D= -198,38 – три действительных различных корня .

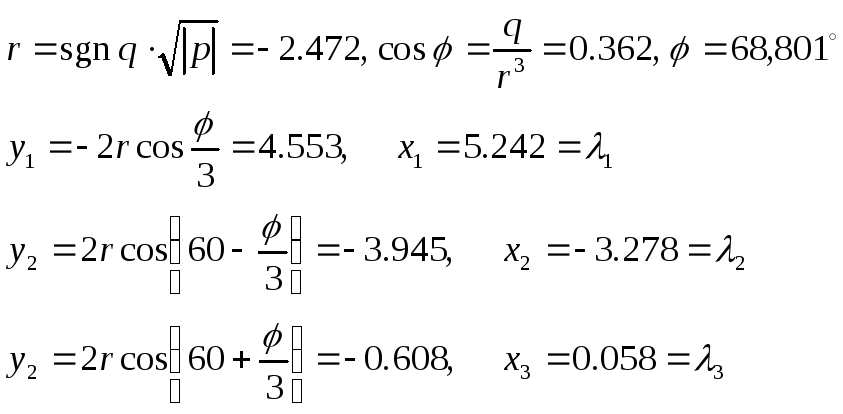
Матрицы и системы ОДУ.

В механике для определения частот свободных колебаний применяется метод решения систем линейных ДУ с постоянными коэффициентами при помощи теории матриц. Также получаемые в результате использования данного метода данные позволяют делать выводы об устойчивости системы .

Рассмотрим систему ОДУ

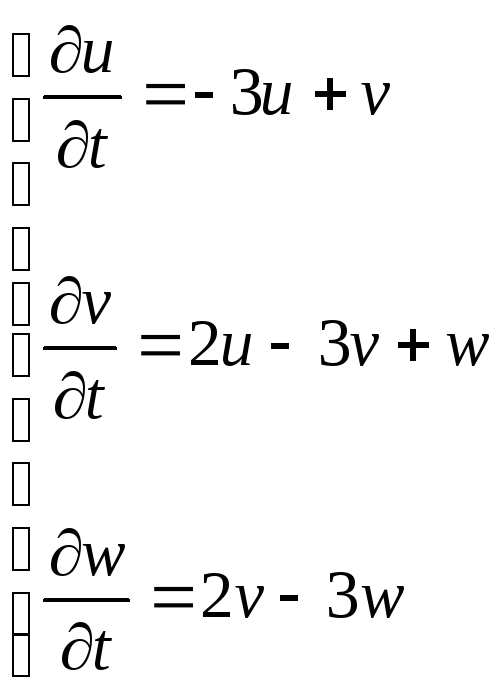
Запишем в виде матрицы А и вектора неизвестных Y

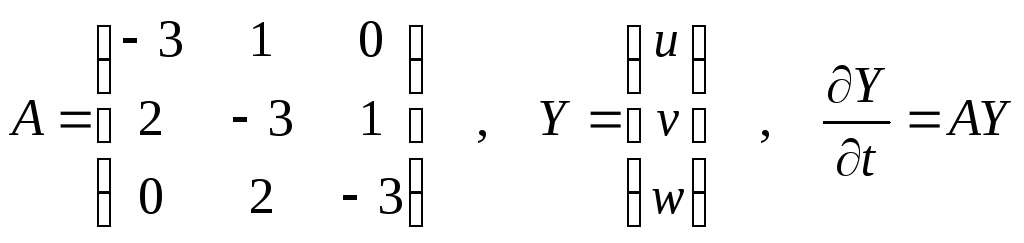
Решение Y ищем в форме

Подставляем предложенное решение в уравнение , имеем

Это основное уравнение относительно собственного числа  и собственного вектора X : , тогда характеристическое уравнение для матрицы А , или

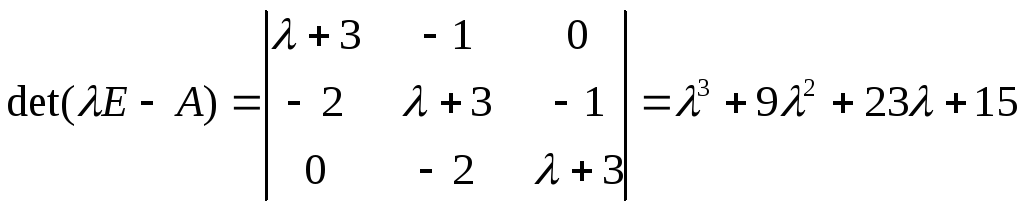
Полученный характеристический полином может быть преобразован:

Определяем собственные вектора ( аналогично рассмотренным примерам)

Получаем вектора ( по порядку, соответственно собственным числам), кратные

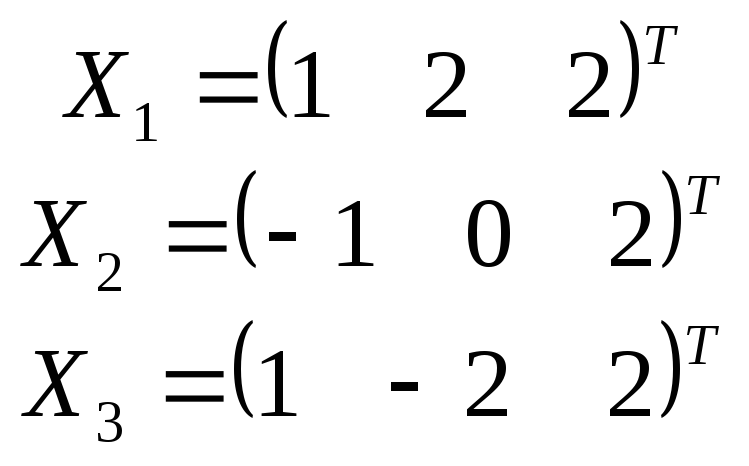
Тогда имеем три чисто экспоненциальных решения:

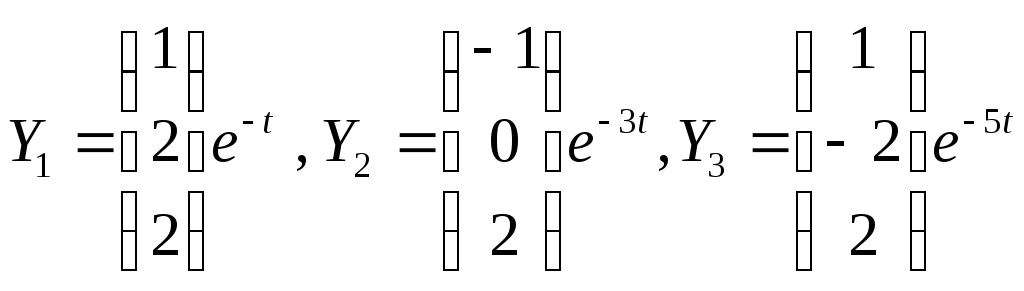
Полученные векторы являются решением линейного и однородного уравнения, следовательно возможна суперпозиция решений , т.е. при произвольных скалярах с₁,с₂,с₃ линейная комбинация тоже будет решением

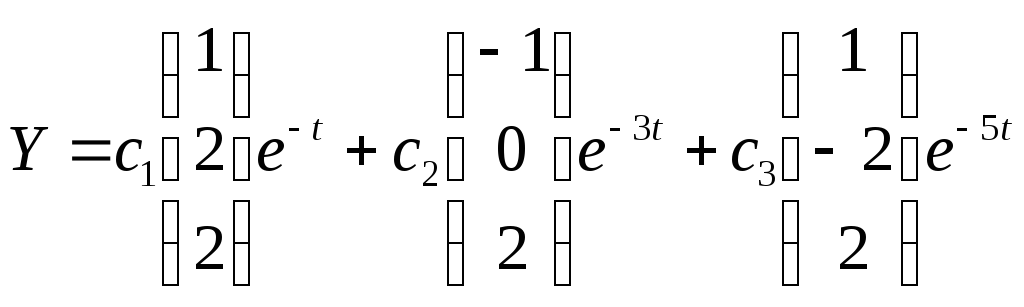
Теперь вопрос , могут ли коэффициенты с₁,с₂,с₃ быть выбраны таким образом , чтобы удовлетворить заданным начальным условиям , например:

При t=0 u=-4,v=4,w=8 , что эквивалентно записи в векторной форме

Или векторное уравнение

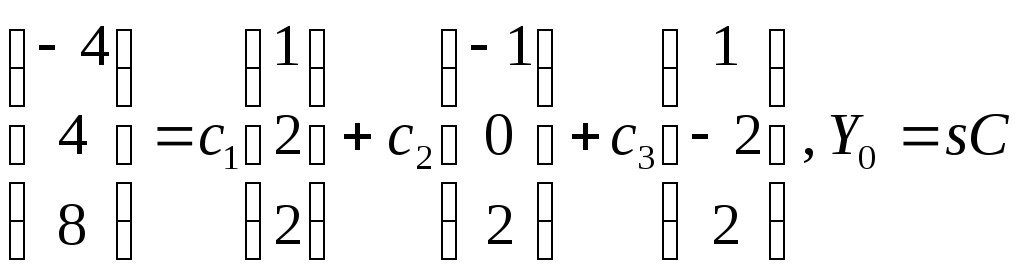
Здесь введено обозначение s-матрица , в столбцах которой расположены собственные вектора, а С- вектор-столбец с произвольными постоянными

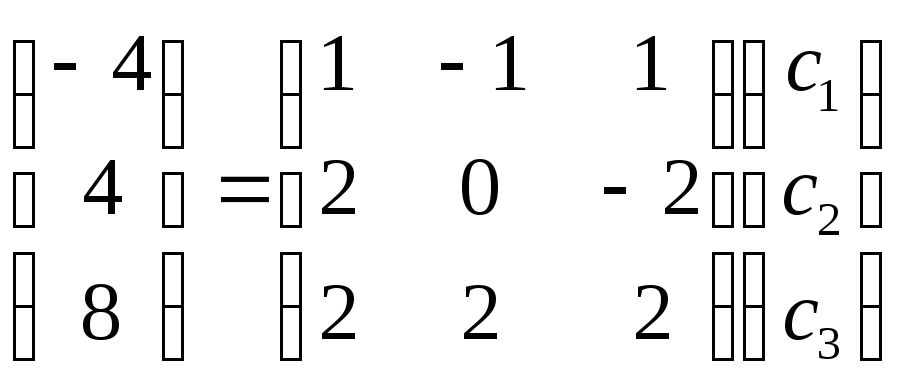
Решая , получаем значения произвольных постоянных

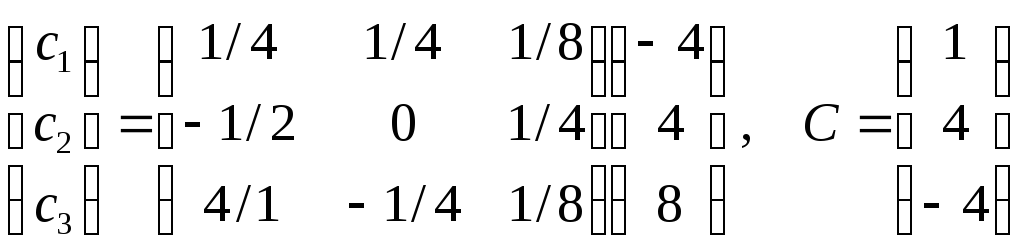
Тогда решение исходного уравнения с учетом начальных условий

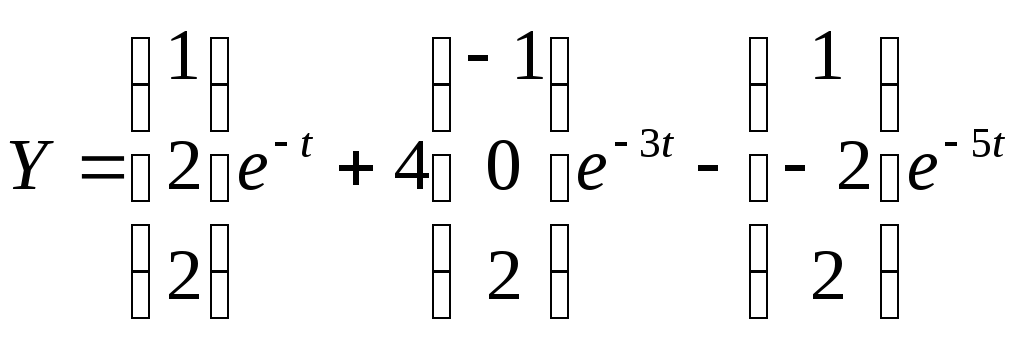
Или отдельно

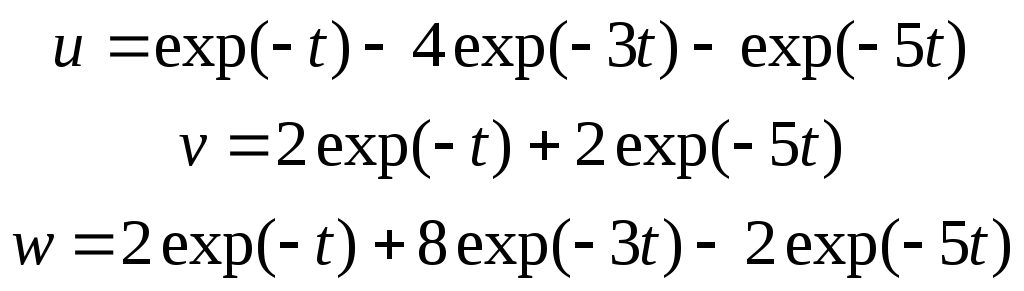
Собственные числа и проблема устойчивости .

Для различных динамических конструкций устойчивость понимается по-разному.

Наиболее важной характеристикой любой динамической системы являются собственные числа.

Рассмотрим линейную динамическую систему с постоянными коэффициентами

, где

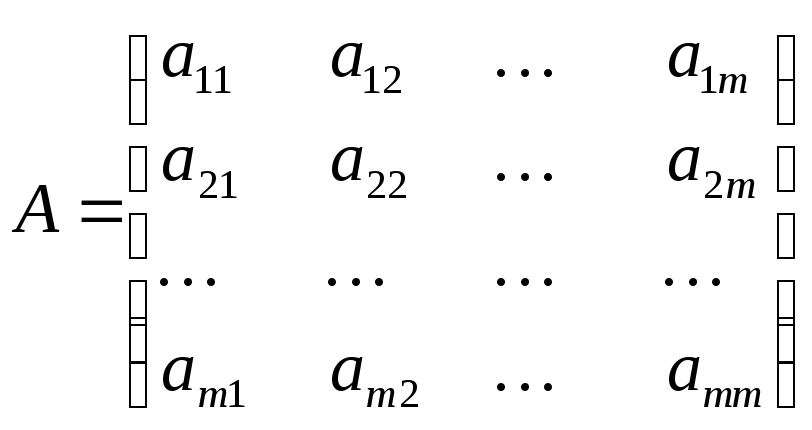
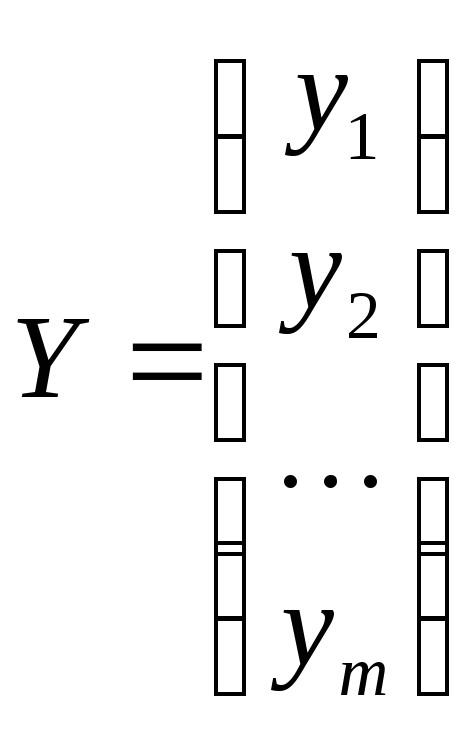
Мы хотим исследовать решение при t.

Как уже известно, любое частное решение ДУ есть некоторая комбинация m экспоненциальных решений ДУ.

Устойчивость определяется множителем exp(t).

Если они стремятся к нулю , то и все решение будет стремиться к нулю ,

Если ограничены- ограничено,

Если хотя бы один из множителей растет- то решение тоже будет расти.

Устойчивость определяется только вещественными частями :

Мнимые части  дают чистые колебания.

Устойчивость по Ляпунову.

Рассмотрим систему ДУ, описывающую динамику системы

Вспомним понятие эвклидовой нормы

Каждое частное решение называем движением.

Начальное значение Y₀(t) – невозмущенное. Дадим начальному значению вектора Y₀ небольшое по модулю приращение и назовем получаемое движение возмущенным.

Определение:

Движение Y₀(t) системы называется устойчивым по Ляпунову , если для каждого >0 найдется >0 такое , что при условии для любого возмущенного движения при всех t>t₀ имеет место неравенство

Если выполняется движение называется асимптотически устойчивым.

Теорема.

Для того, чтобы положение равновесия Y0 было асимптотически устойчивым ,необходимо и достаточно , чтобы все собственные числа матрицы А имели отрицательные вещественные части.

Пример.

Для рассмотренной системы ДУ имеем асимптотическую устойчивость по Ляпунову , поскольку все собственные числа отрицательны.

Теорема Ляпунова

А- постоянная матрица , все собственные числа имеют отрицательные вещественные части и при tt₀ и достаточно малом Y

, где  и М - положительные постоянные. Тогда положение равновесия Y0 системы уравнений асимптотически устойчиво.

Пример

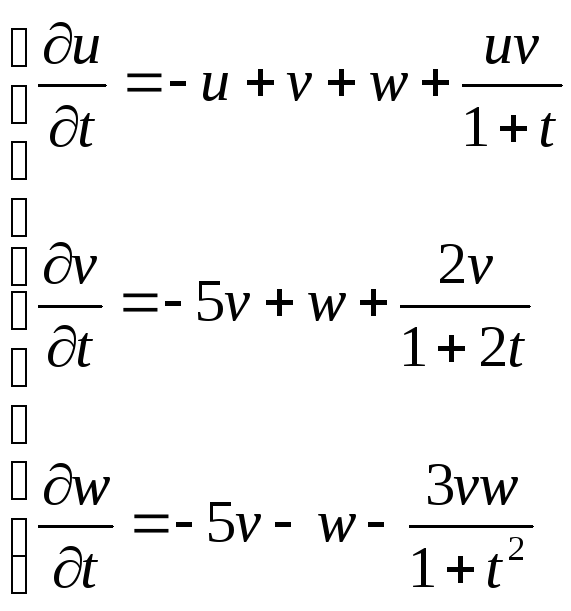
Матрица А имеет вид

11

стр. из 11