Экзамен / TMM_otvety_2

Вопрос 15. Силовой расчет механизмов с учетом трения в КП методом последовательных приближений.

Пример: кривошипно-ползунный механизм.В первом приближении связи считают идеальными, силами трения пренебрегают. По найденным реакциям находят силы трения и повторяют силовой расчет, считая силы трения известными. Вычисляют следующие приближения до тех пор, пока разница между значениями сил реакций, найденных в последующем и предыдущем приближениях, не окажется меньше допустимого значения.

Пример. Будем считать массу шатуна 2 пренебрежимо малой. При сделанном допущении ползун 3 становится статически определимым.

Первое приближение. Полагая силы трения = нулю, запишем уравнения кинетостатики для ползуна:

известной, найти следующее, третье приближение, и т.д.

Вопрос 16. Силовой расчет механизмов с учетом трения в КП. Решение нелинейных уравнений силового анализа. Пример: кривошипно-ползунный механизм. Режимы: тяговый, инверсный тяговый,

оттормаживания, самоторможения. Система уравнений кинетостатики для ползуна:

Вариант 1.2. «Большое» трение; рабочая нагрузка P и сила инерции Ф3 направлены против скорости ползуна.

Получающееся противоречие показывает, что решения не существует. Этот случай соответствует режиму самоторможения, при котором в рассматриваемом положении механизма и при заданном направлении силы движение вообще становится невозможным. Вариант 2.2. «Большое» трение; силы P и Ф3 направлены против оси х («помогают» движению ползуна). Тогда уравнение (5.26) имеет два решения. Действительно,

поскольку числитель положительный, а знаменатель отрицательный. В этом случае мы имеем дело с режимом оттормаживания: при «большом» трении движение возможно в том случае, когда вектор Р + Ф3 направлен так же, как и скорость ползуна. Существование двух режимов оттормаживания является одним из парадоксов Кулонова трения. Установить, какое из решений будет фактически осуществляться, строго говоря, в рамках модели механизма с жесткими звеньями невозможно. Можно только показать, что некоторые «физические» соображения свидетельствуют в пользу первого решения. при увеличении коэффициента трения f следует ожидать увеличения модуля силы трения |F| , т.е. должно быть d|F|/df>0. Исследуя первое решение, получаем

Поэтому второе решение является с физической точки зрения «недостоверным».

Сведем все найденные решения в табл. Для удобства сравнения результатов, полученных двумя методами, разделим числитель и знаменатель дроби выражения (5.26) на ctgα.

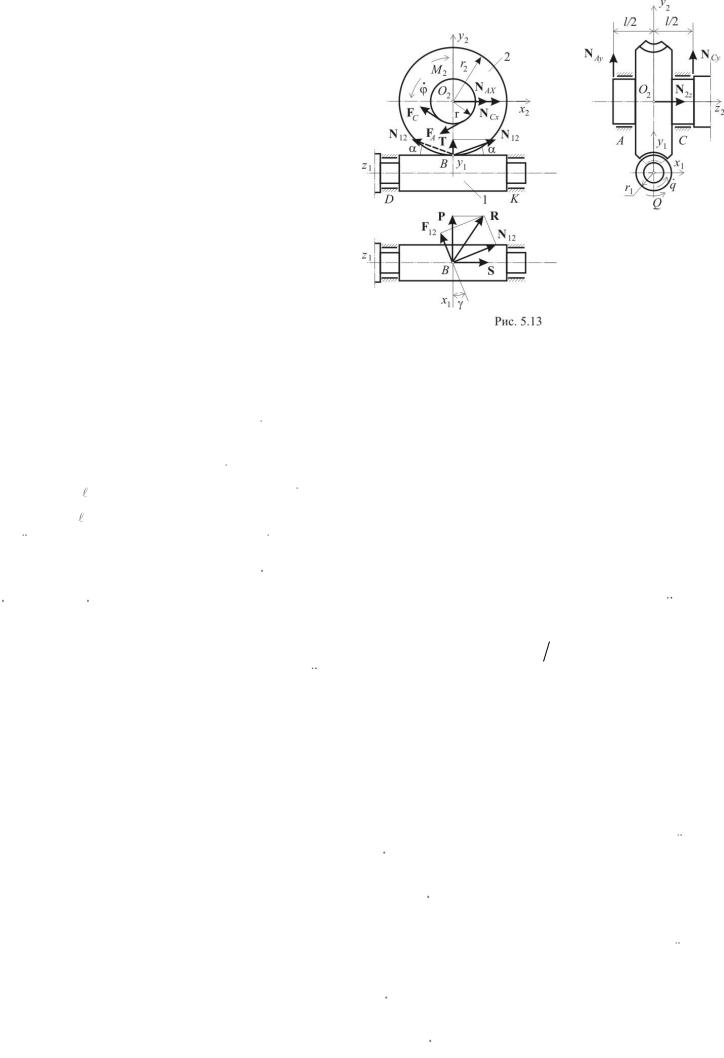
17. Силовой расчет червячной передачи с учетом трения в ВКП. Режимы: тяговый, инверсный тяговый, оттормаживания,

самоторможения.Червячная передача содержит

представляется уравнениями (5.16), и две вращательные пары. Пренебрежем трением во вращательных парах, поскольку оно обычно оказывается значительно менее существенным, чем трение в червячном зацеплении. Сначала составим уравнения кинетостатики для червячного колеса. Положим, что оси координат О2xyz являются главными центральными осями инерции

колеса. Используем соотношения (5.16). Обозначим: r2 – начальный радиус червячного колеса, J20 – момент инерции колеса относительно оси О2z (точка О2 совпадает с центром масс колеса). Проецируя силы, действующие на колесо, на оси координат О2xyz и составляя уравнения моментов относительно этих осей, получаем систему шести уравнений с шестью неизвестными (NAx, NAy, NCx, NCy, N2z, N12):

Пусть направление угловой скорости совпадает с показанным на рисунке:

зависимости от режима движения червячной передачи. Отметим, что для более точного расчета червячной передачи следует учитывать зависимость коэффициента трения и, следовательно, угла трения от скорости скольжения Vск и от режима движения. В табл. приведены значения N12 для разных режимов.

кинетическая энергия механизма, представленная как функция от обобщенной координаты и обобщенной

сопротивления, соответствующая всем активным силам, кроме движущих. В механизме с одной степенью

массой механизма; при угловой обобщенной координате a(q) имеет размерность момента инерции и называется приведенным моментом инерции. В дальнейшем будет предполагаться, что q – угловая

координата, и выражение (6.3) записывается в форме T 12 J( q) q2 ,(6.4) где J(q) – приведенный момент

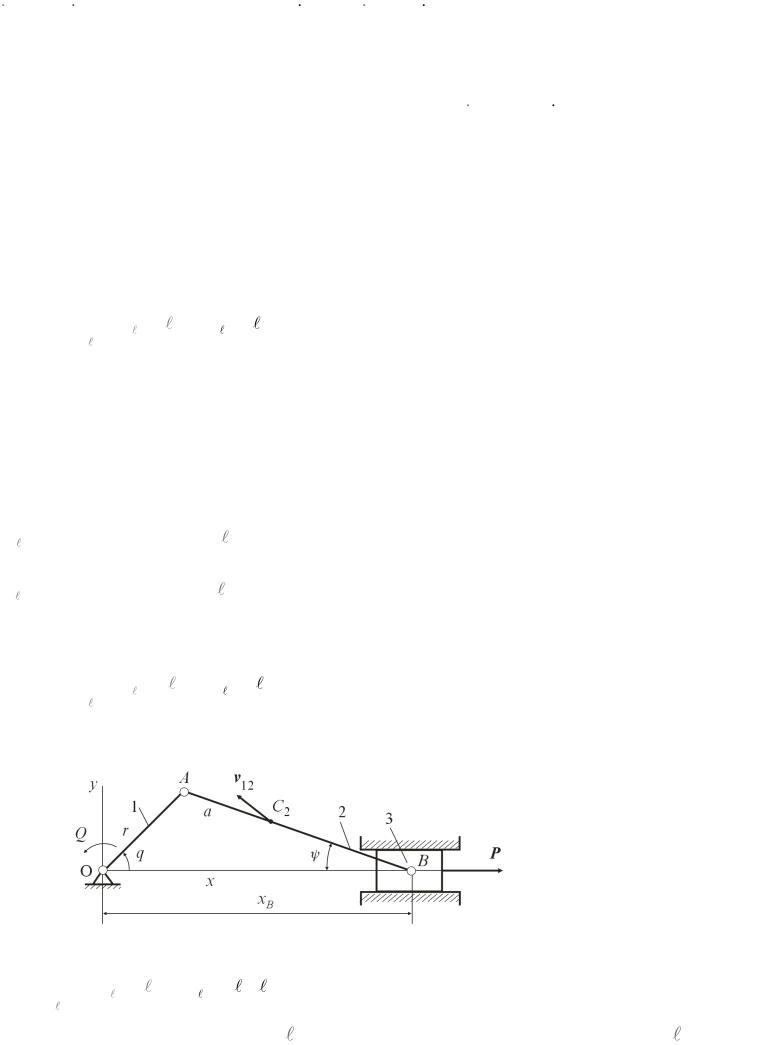
Рассмотрим кривошипно-ползунный механизм, показанный на рис. 6.1.

Кинетическую энергию механизма определяем как сумму кинетических энергий его подвижных звеньев. Для вращающегося звена 1 имеем T1 12 J10q2 ,

где J10 – момент инерции звена относительно оси вращения. Для поступательно движущегося ползуна 3

получаем T3 12 m3 xB2 . Для звена 2, совершающего сложное движение, находим кинетическую энергию,

пользуясь теоремой Кёнига, известной из курса теоретической механики: T2 12 (m2vC2 2 J2C 22 ), где m2 –

масса звена, J2C – его момент инерции относительно оси, проходящей через центр масс С2 и

перпендикулярной плоскости движения; vC2 – скорость центра масс; 2 – угловая скорость. Таким образом, учитывая, что

Выражение, стоящее в фигурных скобках, представляет собой приведенный момент инерции механизма J(q). Используя функции положения xC2(q), yC2(q), (q), xB(q), можно было бы представить J(q) в явной форме; однако это аналитическое выражение даже для такого сравнительно простого рычажного механизма

оказывается достаточно громоздким. Еще более сложным является выражение J (q) . Поэтому на практике часто используются приближенные представления этих функций, основанные на их разложении в ряды Фурье. Легко видеть, что J(q) – периодическая функция с периодом 2 ; она представима в виде ряда:

Для определения коэффициентов Фурье J0, JC1, … , JS1, … вычисляются значения J(q) при некоторых дискретных значениях q, например, при q = 2 k/m (k=1, … m). Для этого используется выражение для J(q) в форме (6.6), а значения производных от функций положения определяются в процессе кинематического анализа механизма. Затем используются известные приближенные соотношения, выражающие

Удовлетворительная аппроксимация для – й гармоники получается только при условии m 4 . Следует также иметь в виду, что пренебрежение высшими гармониками в выражении для приведенного момента