Добавил:

Xer1t Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Санкт-Петербургский политехнический университет Петра Великого (бывш. СПбГПУ)

Предмет:

Теория механизмов и машин

Файл:

Экзамен / TMM_otvety_2

.pdf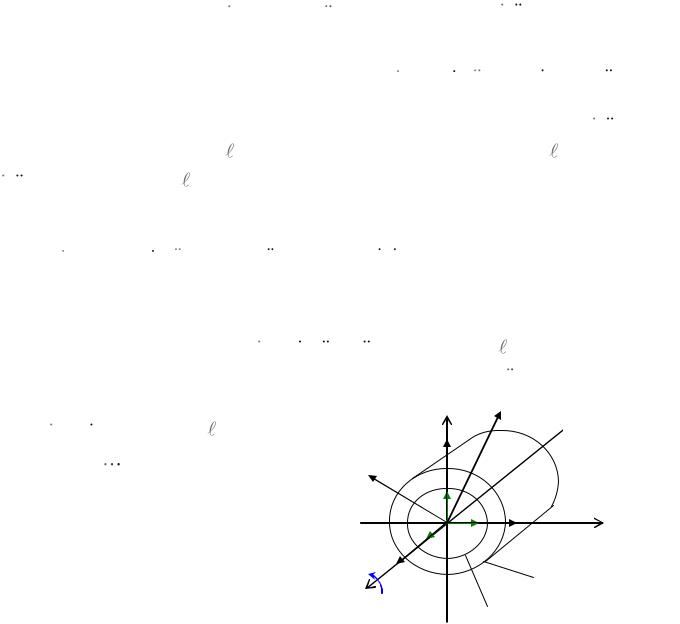

Скачиваний:

Добавлен:

26.11.2019

Размер:

3.61 Mб

Скачать

☆

1 / 61 2 3 4 5 6 > Следующая >>>

Билет №1. Постановка задачи силового расчета. Силы, действующие в механизме. Уравнения движения системы. Кинематические пары, накладывающие идеальные связи. В теории механизмов и машин также ставятся и решаются две задачи динамики. В частности, первая задача динамики: при известном (заданном) законе движения ведущего звена (ведущих звеньев) механизма требуется найти силы, действующие в механизме. Решение этой задачи называют силовым расчетом. При силовом расчете механизма считаются известными все активные силы, действующие на звенья механизма, кроме обобщенных движущих сил. К заданным активным силам относятся: а) Рабочая нагрузка P – сила,

действующая на рабочее звено при выполнении рабочего процесса. Рабочая нагрузка обычно не является постоянной. Часто она изменяется по мере перемещения рабочего звена. В этом случае может быть построена зависимость Р = Р(х), где Р – рабочая нагрузка, х – координата точки приложения нагрузки. В более сложных случаях нагрузка зависит также от скорости x , ускорения x и времени t: P P(x, x, x,t) . Эти зависимости изучаются в специальных дисциплинах. При выполнении силового расчета они считаются заданными, но их


следует привести к более удобному виду. Учитывая, что x (q),	x		q ,	x	2		q2		q , можно
	x	q	q ,	x	q	2	q2		q , можно
		q				2
								q

получить зависимость рабочей нагрузки от обобщенной координаты и ее производных: P P* (q,q,q,t) .(4.1)

Если в механизме приложена не одна,			а	рабочих нагрузок, то для них задаются	зависимостей:
P	P* (q,q,q,t) , (m = 1,	2, … , ).	(4.2) В многоподвижных механизмах координаты, скорости и
m	m
ускорения точек приложения		нагрузок	Pm	зависят от всех обобщенных координат и	производных:

xs s

где s

w		w		w		s
(q1,...,qw ); xs	s qu ; xs		s qu			s	qu qm , (4.3)
					2
			q		q q
	q	u 1	q	m 1	q q
	u		u		u m
u 1

– функции положения. Зная (4.3), можно получить зависимости рабочих нагрузок от обобщенных

координат и их производных: P	P* (q ,...,q ,q ,...,q ,q ,...,q ,t) , (m = 1, … , ) . (4.4) В дальнейшем
m	m 1	w 1	w 1	w

будем предполагать, что рабочие нагрузки не зависят явно от времени и ускорений qu , поэтому выражения (4.4) будут представляться в форме:

P	P* (q ,...,q ,q ,...,q ) ,			(m = 1, … , ) (4.5) (б) Cилы
m	m 1	w 1	w
тяжести звеньев Gi,			i 1,	, N , где N – число звеньев..в)

Упругие силы, возникающие при деформации пружин, также являются активными. Целью силового расчета является определение обобщенных движущих сил и реакций во всех кинематических парах. Обобщенные движущие силы – это обобщенные силы, которые необходимо приложить к входным звеньям механизма для того, чтобы получить заданное программное движение при выполнении рабочего процесса. Определив движущие силы, можно выбрать двигатели, приводящие в движение машину.Реакции в

Y		MR
M 0Ry		0
M 0Ry
R
Ry		M 0Rx
0	R	X
0	R
M R Rz
0 z		1
z		1
z		2
Z		2

Рис. 4.1

кинематических парах – пассивные силы; как правило, это силы, распределенные по поверхностям соприкосновения конструктивных элементов, образующих пару. Рассмотрим вращательную кинематическую

пару (рис.4.1); главный вектор сил реакций R и главный момент M0R определяются заданием шести скалярных величин – их проекций Rx , Ry , Rz , MoxR , M0Ry , M0Rz на оси системы 0xyz. Число неизвестных

обобщенных движущих сил равно w, а число неизвестных компонент реакций – 6p. Таким образом, общее число неизвестных

nu = w + 6p = w + 6p1 + 6p2 + 6p3 + 6p4 + 6p5 . (4.6) Эти неизвестные могут быть определены решением уравнений движения звеньев механизма. Пусть число звеньев равно N. Если KS – вектор количества движения s–го звена, а LSO – его кинетический момент, то уравнения движения записываются в виде:

dKS

dLS 0

Fsk ;

rsk Fsk ,(s 1,..., N 1), (4.7)

где Fsk

– внешние силы, действующие на s–е

k 1

звено, rsk – радиусы-векторы точек их приложения, gs

– число сил, приложенных к s–му звену. Пусть

механизм

не

содержит

избыточных

связей.

Тогда

для

него

справедлива формул

w 6(N 1) (6

s) pS

S 1

(4.8)

6(N 1) 5 p1 4 p2 3 p3 2 p4 p5 ,

где ps– число s–подвижных пар. Из уравнения (4.8) можно выразить

число

уравнений neq = 6(N–1):

6(N 1) w 5 p1 4 p2 3p3 2 p4 p5 .

Сравнивая число неизвестных nu

и число уравнений neq ,

имеем: nu

neq

2 p2 3 p3 4 p4 5 p5 spS . (4.9)

S 1

При такой постановке задачи силового расчета число неизвестных всегда больше числа уравнений, что делает эту задачу неразрешимой. Она тем более неразрешима, если в механизме имеются избыточные связи, поскольку при этом число неизвестных реакций возрастает, а число уравнений остается неизменным.

Для того, чтобы задача стала разрешимой, необходимы дальнейшие уточнения. Одно из таких уточнений заключается в предположении о том, что все кинематические пары осуществляют идеальные связи. При идеальных связях работа сил реакций каждой кинематической пары должна равняться нулю при любом возможном перемещении, т.е. должно быть

A R

x R y R

z M R

M R

(4.10) Здесь

x, y, z

– малые

0 X

возможные перемещения вдоль осей координат,

а X , Y , Z – малые повороты вокруг этих осей.

Вращательная пара (см. рис.4.1) допускает только малый поворот звена 2 (цапфы) относительно звена 1

(втулки) вокруг оси 0z. Тогда из (4.10) имеем A M0RZ Z 0. Поскольку при повороте Z 0, имеем

M0RZ 0. Таким образом, одна из шести компонент реакций вращательной пары определилась, и число неизвестных уменьшилось на единицу – степень подвижности пары. В поступательной паре возможное перемещение ползуна относительно направляющей направлено вдоль оси х. Поэтому здесь A RX x 0,

и поскольку x 0, имеем RX 0 , что также определяет одну из неизвестных компонент реакций. В

цилиндрической паре отличны от нуля возможные перемещения Z (поворот вокруг продольной оси 0z) и

z (перемещение вдоль этой оси),	так что здесь	A R	z M R	Z	0.	В	силу независимости
		Z	0Z	Z
возможных перемещений z и Z	это условие должно выполняться как при z 0,						Z 0, так и при

z 0, Z 0. Это приводит к выводу о том, что RZ и M0RZ должны равняться нулю, что определяет для двухподвижной цилиндрической пары две компоненты реакций. Аналогично можно показать, что в любой s–

подвижной паре условие идеальности приводит к появлению s	дополнительных	соотношений для
	5
компонент реакций. В результате для механизма в целом появляется	spS условий,	что делает задачу
	S 1

силового расчета разрешимой. Часто в этом случае говорят о статической определимости механизма.

Билет №2 Уравнения кинетостатики.Уравнения (4.7) удобно представить в другой форме. Введем в

рассмотрение	силы	инерции	материальных	точек	s–го	звена
Φsi msiwsi ,	(i 1, ... ks , s 1, ... N 1),		(4.11) где msi – масса i–й материальной точки; wsi			– ее
ускорение. Напомним, что «сила инерции» Φsi лишь условно называется силой; в действительности это

мера движения материальной точки, подобная, например, количеству движения. Вводя силы инерции,

можно преобразовать левые части уравнений (4.7); учитывая, что KS msi vsi, Ls0

rsi msi vsi ,

получаем

dKS

msi vsi

msi wsi Φsi ΦS ,

(4.12)

dLS 0

rsi msi vsi (vsi msi vsi

rsi msiwsi ) rsi Φsi M0( S ). (4.13)

Здесь Φ

– главный вектор сил инерции s–го звена, а M( )

– их главный момент относительно некоторой

произвольно выбранной точки О. В правых частях уравнений (4.7) выделим активные силы PSK и реакции

кинематических пар RSK :

FSK (PSK RSK ) PS RS ,

(4.14) где PS и RS – главные векторы активных сил и

rSK FSK rSK (PSK RSK ) M0( PS) M(0RS) ,

реакций связей, действующих на s–е звено, M0(PS) и M0(RS) –

их главные моменты относительно точки О.

Подставив (4.14) в (4.7), получим уравнения движения в следующей форме:

P R

M(P) M(R) M( )

0. (s 1,..., N) . (4.15) Уравнения движения получили форму

уравнений равновесия. Можно сказать, исходя из этой формы, что активные силы, действующие на каждое из подвижных звеньев механизма, реакции связей и силы инерции звена образуют уравновешенную системую. В действительности силы инерции силами не являются; они являются мерами движения. Соответственно уравнения (4.15) являются уравнениями движения. Чтобы подчеркнуть это обстоятельство, их называют уравнениями кинетостатики, а модель силового расчета механизма, основанную на их применении, –

кинетостатической моделью.

Билет №3-4 Определение главного вектора и главного момента сил инерции (общий случай; поступательное движение; вращение вокруг неподвижной оси; плоское движение) Уравнения (4.7)

удобно представить в другой форме. Введем в рассмотрение силы инерции материальных точек s–го звена Φsi msiwsi , (i 1, ... ks , s 1, ... N 1), (4.11) где msi – масса i–й материальной точки; wsi – ее ускорение. Напомним, что «сила инерции» Φsi лишь условно называется силой; в действительности это мера движения материальной точки, подобная, например, количеству движения. Вводя силы инерции,

можно преобразовать левые части уравнений (4.7);

учитывая, что

KS msi vsi, Ls0

rsi msi vsi ,

получаем

dKS

msi vsi msi wsi Φsi ΦS ,

(4.12)

dLS 0

rsi

msi vsi (vsi msi vsi rsi msiwsi ) rsi Φsi M0( S ). (4.13)

Здесь Φ	– главный вектор сил инерции s–го звена, а M( )		– их главный момент относительно некоторой
S		0S
произвольно выбранной точки О. В правых частях уравнений (4.7) выделим активные силы PSK и реакции
кинематических пар RSK :
FSK (PSK RSK ) PS RS ,
K	K	(4.14) где PS		и RS – главные векторы активных сил
rSK FSK rSK (PSK RSK ) M0( PS) M(0RS) ,		(4.14) где PS		и RS – главные векторы активных сил
rSK FSK rSK (PSK RSK ) M0( PS) M(0RS) ,
K	K

и реакций связей, действующих на s–е звено, M(0PS) и M(0RS) – их главные моменты относительно точки О. Подставив (4.14) в (4.7), получим уравнения движения в следующей форме:

PS RS ΦS 0; M(0PS) M(0RS) M(0S ) 0. (s 1,..., N) . (4.15) Уравнения движения получили форму

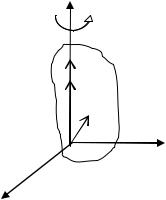
уравнений равновесия. Можно сказать, исходя из этой формы, что активные силы, действующие на каждое из подвижных звеньев механизма, реакции связей и силы инерции звена образуют уравновешенную систему. Следует только помнить об условности такой формулировки; в действительности силы инерции силами не являются; они являются мерами движения. Соответственно уравнения (4.15) являются уравнениями движения, а не уравнениями равновесия. Чтобы подчеркнуть это обстоятельство, их называют уравнениями кинетостатики, а модель силового расчета механизма, основанную на их применении, – кинетостатической моделью. Для составления уравнений в форме (4.15) необходимо уметь определять главные векторы и главные моменты сил инерции звена при заданном законе его движения. Пусть некоторая

точка О (рис.4.2) выбрана за полюс звена, rc –			вектор, определяющий положение его центра масс С. Если
известны ускорение полюса w0 , вектор угловой скорости звена ω и вектор его углового ускорения ε (они
определяются при кинематическом анализе механизма), то для главного вектора сил инерции										Φ и для
главного момента их M( )	относительно точки О справедливы следующие выражения:
0
		mwC m(w0			rC rC ),					(4.16)
		M(Φ)	(I ε ω I		ω mr w			0	). (4.17)
		0		0	0	C		0
z		Здесь m – масса звена, I0 – тензор инерции в точке О. Если ввести
		систему координат 0хyz, связанную со звеном, то тензор I0 можно
	C	задавать матрицей моментов инерции
	C			J XY	J XZ
w0			J X	J XY	J XZ
w0	r		J XY		JYZ
	C			JY
0	y	I0		JY		,	(4.18)
			J XZ	JYZ	JZ
			J XZ	JYZ	JZ
x
Рис. 4.2		где JX, JY, JZ – осевые, а JXY, JYZ, JXZ – центробежные моменты
Рис. 4.2		инерции. Найдем выражения					для		проекций на оси	главного
		инерции. Найдем выражения					для		проекций на оси	главного

вектора и главного момента сил инерции в некоторых частных случаях.

a). Поступательное движение звена. Учитывая, что ω=0, ε=0, найдем M(0Ф) :

	i	j	k
M(Ф) m	x	y	z	c
0	c	c		c
	wox	woy	woz
m i ycwoz zc woy j zcwoz xc woz k xcwoy yc wox					.

Здесь хс, yc, zc – координаты центра масс. Тогда:

Фx m wox ,Фy m woy ,Фz m woz , M0(Фx ) m yc woz zc woy ,

(4.19)

M0(Фy ) m zc woz xc woz ,

M0(Фy ) m xc woy yc wox .

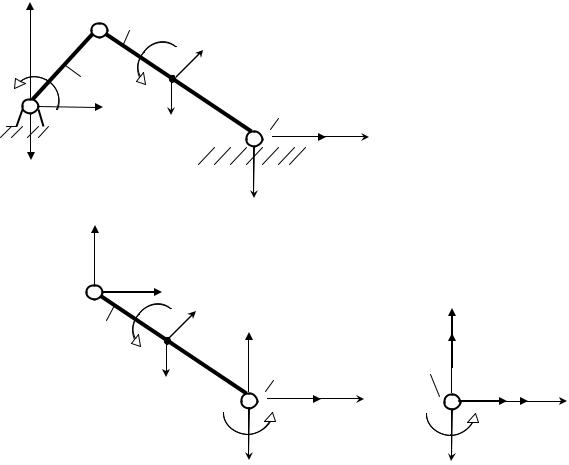
б). Вращение вокруг неподвижной оси (рис.4.3).

ωх = ωy = 0; ωz = ω; εx = εy = 0; εz = ε; w0 = 0.

Для определения главного вектора сил инерции найдем векторные произведения:

	i	j		k
ε rc	0	0			i ( yc ) j ( xc ) k (0) ,
	xc	yc		zc
				i		j	k
				i		j	k
ω (ω r )				0		0		i ( 2 x ) j ( 2	y ) k (0) .
	c							c	c
			yc			xc	0

Отсюда найдем проекции главного вектора сил инерции:

Ф m (x 2		y ),
x	c	c
Фy m ( yc 2		xc ), (4.20)
Фz	0.
Для определения главного момента сил инерции найдем I0 ε и ω I0ω :
			Ixz
			I yz
		Ioε	I yz	,
			Iz
			Iz

i ( 2 I yz ) j ( 2 Ixz ) k 0.

ω Ioω

Подставляя найденные соотношения в выражение (4.17), найдем главный

момент сил инерции в проекциях на координатные оси:

M ox(Ф) I yz 2 Ixz ,

M oy(Ф) Ixz 2 I yz ,

(4.21)

(Ф) I

rc y

Рис. 4.3

в). Плоское движение звена. Выберем в качестве полюса центр масс звена С. Введем систему координат Сxyz так, чтобы ось Сz была перпендикулярна плоскости движения звена. В осях Cxyz построим тензор инерции IС:

	J C	J C	J C
	X	XY	XZ
IC	J XYC	JYC	JYZC	.
	J C	J C	J C
	J C	J C	J C
	XZ	YZ	Z

Тогда получим следующие выражения для главного вектора и главного момента сил инерции:

Ф mw			M ox(Ф) I yz (c) 2 I xz(c)
x		cx
Ф	y	mw	, M	oy	(Ф) I	(c) 2	I	(c) (4.22)
	y	cy		oy		xz		yz
Фz mwcz			M oz (Ф) Iz

Билет №5-6. Силовой расчет плоских рычажных механизмов (одноподвижных и многоподвижных). Примеры. Для механизмов с идеальными связями уравнения кинетостатики представляют собой систему линейных алгебраических уравнений, обладающую единственным решением, если избыточные связи в системе отсутствуют, а рассматриваемое положение механизма не является особым. Для сложных механизмов, содержащих большое число подвижных звеньев, система уравнений кинетостатики имеет высокий порядок (для N–1 подвижных звеньев – 6(ּN–1) уравнений). Ее решение существенно облегчается тем, что она может быть разделена на несколько независимых систем, каждая из которых содержит обобщенную движущую силу и реакции кинематических пар, действующие на звенья одной структурной группы. Действительно, для каждой структурной группы, не содержащей избыточных связей, справедлива структурная формула

5
wG 6NG (6	s) pSG , (4.23) где wG – число степеней подвижности группы, NG – число подвижных
S 1

звеньев группы, pSG – число s-подвижных кинематических пар в группе. С другой стороны, как было показано выше, сумма

5
nu wG (6	s) pSG (4.24) представляет собой число неизвестных движущих сил и реакций в
S 1

идеальных связях, подлежащих определению. Сравнивая выражения (4.23) и (4.24), замечаем, что nu=6NG, т.е. число неизвестных сил равно числу уравнений кинетостатики. Таким образом, уравнения кинетостатики могут решаться последовательно для каждой структурной группы. Особенности расчета плоского механизма. В плоском механизме, выделяя последовательно плоские структурные группы, можно для

каждой из них определить отдельно компоненты реакций, лежащих в плоскости движения х0y (Rx, Ry, M0RZ ), и обобщенные движущие силы. Часто из-за наличия избыточных связей определение всех реакций второй группы (Rz, M0RX , M0RY ) становится невозможным; в этом случае приходится ограничиваться определением

только реакций освобождающих связей.

а) На рис.4.4 показан плоский механизм с одной степенью подвижности, состоящий из двух структурных

групп:

однозвенной

одноподвижной

группы

(звено 1) и

группы Ассура

типа ВВП (звенья 2 и 3).

Ф2

На рисунке нанесены активные силы:

заданные ( P, G1, G2, G3) и

( Ф )

подлежащие

определению

(движущий момент Q), а также силы

M S 2

Ф3

инерции,

лежащие

в плоскости

движения (Φ2 ,Φ3) , и проекции

моментов сил инерции на ось z,

перпендикулярную

плоскости

R12yРис. 4.4

б)

R12x

Ф2

R03

R23y

M S( Ф2

)

Ф3

R23x Р

Ф3

M 03( R )

( R )

M03

Рис. 4.5

движения ( M S(Ф2 ) ). Силовой расчет начинается с последней группы, т.е. группы Ассура ВВП (рис.4.5, а). На

рисунке показаны компоненты реакций, лежащие в плоскости движения. Во вращательных парах (например, в шарнире А) возникают реакции с компонентами Rx и Ry, а в поступательных парах (например, в

поступательной паре В) – нормальная реакция R и момент M0(Rz ) . В шарнире А со стороны звена 1 на звено 2

действуют компоненты реакции R12x и R12y, а в поступательной паре В стороны стойки 0 на ползун 3 действуют реакция R03 и момент M03(R) .

Реакция в шарнире В является внутренней для группы, поэтому она на не показана. Для того, чтобы включить в рассмотрение реакцию в В, надо отбросить либо звено 2, либо звено 3. На рис.4.5, б оставлено (ползун); к указанным ранее силам добавлены компоненты реакции R23x действующей со стороны звена 2 на звено 3. Таким образом, в группе плоскости, перпендикулярной оси z, всего 6 неизвестных: R12x, R12y, R23x,

M03(R) . Для звена 3 из условия равенства нулю суммы моментов всех сил относительно оси Bz (т.е. оси z, проходящей через точку B) следует:

M03(R) 0 .

		R21y		со

y	A		рисунке
			шарнире
R01y
		R21x звено		3
Q	1		и R23y,
			ВВП	в

O	R01x x		R23y, R03,

Рис. 4.6

Сумма моментов всех сил, действующих на звенья 2 и 3, относительно оси Аz:

(Р + Ф3)(yA – yB) – (R03 – G3)(xA – xB) + Ф2x(yA – yS2) – (Ф2y – G2)(xA – xS2) + M S(Ф2 ) = 0,

где Ф2х и Ф2y – проекции главного вектора сил инерции второго звена, хА, yA, xB, yB, xS2, yS2 – координаты точек соответственно А, В, S2. Отсюда можно найти реакцию R03. После этого легко определяются остальные

неизвестные. Уравнения для ползуна 3: R23x + P + Ф3 = 0, R03 + R23y – G3 = 0. Уравнения для звеньев 2 и 3:R12x + Ф2x + P + Ф3 = 0;

R12y + Ф2y – G2 + R03 – G3 = 0. После определения всех реакций в группе ВВП переходят к расчету первой структурной группы (рис.4.6). R12x=–R21x, R12y=–R21y. Остаются три неизвестные: компоненты реакции R01x, R01y в шарнире 0 и движущий момент Q. Для кривошипа можно составить три уравнения кинетостатики. Если угловая скорость вращения кривошипа постоянна и центр масс находится на оси вращения О

R21x + R01x = 0, R21y + R01y – G1 = 0, R21x(y0 – yA) – R21y(x0 – xA) + Q = 0.

Последовательность силового расчета проиллюстрирована на схеме рис.4.7.

Предварительно определяются силы инерции Φ2 ,Φ3, MS(Ф2 ) . Потом решаются 6 уравнений для звеньев 2 и 3

группы ВВП, входящей во второй слой, находятся реакции R12x, R12y, R23x, R23y, R03, M03(R) . Затем решаются три уравнения для звена 1, являющегося группой первого слоя. Реакции R21x и R21y рассматриваются как известные (R12x = – R21x, R12y = – R21y). Определяются реакции R01x, R01y и движущий момент Q.

	Ф2 Ф3		( Ф )		G1
	Ф2 Ф3		M S 2
P				R12X = – R21X		R01X, R01Y, Q
				R12X = – R21X
					Звено 1
G2, G3		Группа BBП
		Группа BBП
		(звенья 2,3)			(кривошип)
		(звенья 2,3)		R12Y = – R21Y	(кривошип)



		R03, M03( R ) , R23X, R23Y

Рис.4.7

Рис. 4.8

6б) Механизм с тремя степенями подвижности (рис.4.8). Данный механизм состоит из трех одноподвижных групп: двух однозвенных (звенья 1 и 5) и одной трехзвенной (звенья 2, 3, 4). Определив силы инерции и моменты сил инерции звеньев, а также задав значения активных сил P3X и P3Y, приложенных в точке С3 звена 3, и момента Мw, приступаем к силовому расчету последней структурной группы АВСD. Для плоской системы сил, действующих на три звена этой группы, составляем 9 уравнений кинетостатики, из

которых определяем обобщенную движущую силу Q2 и 8 реакций (R12X, R12Y, R23X, R23Y, R34X, R34Y, R54X, R54Y). Затем приступаем к расчету однозвенных групп первого слоя ОА и ЕD. При этом силы R21X = – R12X, R21Y = –

R12Y, R45X = – R54X, R45Y = – R54Y рассматриваются уже как известные, найденные на предыдущем этапе. Из уравнений кинетостатики для звена ОА определяем R01X, R01Y,обобщенную движущую силу Q1; из уравнений, составленных для звена ЕD,определяем R05X, R05Y,обобщенную движущую силу Q3.

На рис.4.9 схематично представлен алгоритм силового расчета этого механизма. Для каждой группы указаны заданные («входные») силы и силы, найденные при силовом расчете.

Силовой расчет по кинетостатической модели может производиться не только решением уравнений

кинетостатики, составленных для каждого звена в отдельности, но и с помощью других методов. Рассмотрим,

Рис. 4.9

каким образом можно провести расчет трехзвенной группы АВСD, показанной на рис.4.8, методом размыкания кинематической цепи. Разомкнем кинематическую цепь в шарнире D и введем реакции освобождающих связей R54X и R54Y. Составим уравнения равновесия моментов всех активных сил, всех сил инерции и введенных реакций связей относительно осей шарниров А, В, С. Получим три уравнения:

M A ( 2 ) M A (G2 ) M 2(C ) M A (P3 X ) M A (P3Y ) M w M A ( 3 ) M A (G3 )

M3(C ) M A ( 4 ) M A (G4 ) M 4(C ) M A (R54 X ) M A (R54Y ) 0,

M B (P3 X ) M B (P3Y ) M w M B ( 3 ) M B (G3 )

M3(C ) M B ( 4 ) M B (G4 ) M 4(C ) M B (R54 X ) M B (R54Y ) 0,

MC ( 4 ) MC (G4 ) M 4(C ) MC (R54 X ) MC (R54Y ) Q2 0.

Из этих уравнений определяются три неизвестные величины: R54X, R54Y и Q2. После этого определение реакций в шарнирах А, В, С не вызывает затруднений; их можно найти, например, из уравнений проекций на оси х и y сил, действующих на звенья 2, 3, 4. Решение уравнений кинетостатики усложняется, если в механизме имеются избыточные связи. В этом случае система становится статически неопределимой.

1 / 61 2 3 4 5 6 > Следующая >>>

Соседние файлы в папке Экзамен

#
26.11.20191.33 Mб17TMM_otvety_1.pdf
#
26.11.20193.61 Mб14TMM_otvety_2.pdf
#
26.11.20191.42 Mб9zadachi_TMM.doc
#
26.11.201943.52 Кб14Вопросы.xls