4 Средние показатели рядов динамики

Для получения обобщающих показателей динамики социально-экономических явлений рассчитываются средние величины: средний уровень ряда динамики, средний абсолютный прирост, средний темп роста и прироста.

Средний уровень ряда динамики характеризует типическую величину абсолютных уровней. Методы расчета этого показателя зависят от вида ряда динамики.

В интервальном ряду динамики с равноотстоящими уровнями во времени расчет производится по формуле средней арифметической простой:

.

(7.1)

Так, в таблице 7.8 приведен интервальный ряд динамики с равноотстоящими уровнями. Среднегодовой уровень производства обуви за 1992-1997гг. будет равен 93,2 млн. пар, т.е. = 559/6.

Если интервальный ряд имеет неравноотстоящие уровни, то средний уровень ряда вычисляется по формуле средней арифметической взвешенной:

,

(7.2)

где t - длительность интервала времени между уровнями.

Пример: С 01.04.99 по 20.04.99г. в списочном составе работников предприятия числилось 190 человек, с 21.04.99 и до конца месяца -186 человек.

Среднедневная (списочная) численность работников составит:

человек.

Для моментного ряда с равноотстоящими уровнями средняя хронологическая рассчитывается по формуле:

,

(7.3)

где n - число уровней ряда.

Так, в таблице 7.2 приведен моментный ряд динамики с равноотстоящими уровнями.

Среднеквартальные остатки вкладов населения будут определены следующим образом:

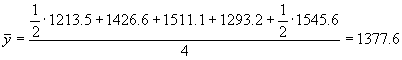млн. руб.

Средний уровень моментных рядов динамики с неравноотстоящими уровнями определяется по средней хронологической взвешенной

.

(7.4)

Покажем расчет среднего уровня такого ряда.

Пример:

Известна списочная численность работников (человек) на:

01.01.98		01.03.98		01.05.98		01.08.98		01.01.99
200		195		190		181		194

Среднегодовая численность работников за 1999 год составит;

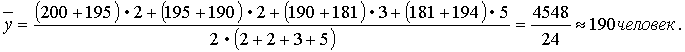
Средний абсолютный прирост рассчитывается по формулам:

(7.5)

или

,

(7.6)

где n - число абсолютных приростов цепных; n-1 - число уровней ряда.

Так, по данным пример, приведенного в таблице 7.8 средний абсолютный прирост равен - 37,8 млн. пар [(31-220):5].

Средний темп роста.

,

(7.7)

где К - средний коэффициент роста, рассчитанный по формулам:

(7.8)

или

,

(7.9)

где n - число индивидуальных цепных коэффициентов роста; n-1 - число уровней ряда.

Например, средний темп роста производства обуви за 1992-1997гг. (табл. 7.8) составит:

Средний темп прироста определяется по формуле:

.
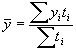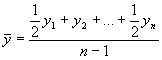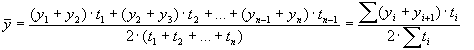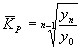