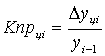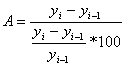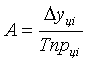3 Статистические показатели изменения уровней ряда динамики
Динамические ряды анализируются при помощи ряда показателей, определяющих направление, характер и интенсивность количественных изменений явлений во времени.
К таким показателям относятся: абсолютный прирост, темп роста и прироста, абсолютное значение одного процента прироста.
В зависимости от принятого способа сравнения показатели динамики вычисляются на постоянной и переменной базах сравнения.
Для расчета показателей динамики на постоянной базе каждый уровень ряда сравнивается с одним и тем же базисным уровнем; исчисленные при этом показатели называются базисными.
Для расчета показателей динамики на переменной базе каждый последующий уровень сравнивается с предыдущим; исчисленные при этом показатели называются цепными. При этих расчетах сравниваемый уровень называют отчетным, а уровень с которым производят сравнение базисным.
Базисный уровень ряда динамики обозначается yо, каждый уровень ряда - yi, конечный уровень ряда - yn.
Рассчитываются показатели динамики по формулам представленным в таблице 7.
Таблица 7 - Показатели изменения уровней ряда динамики
Показатель |
Базисный |
Цепной |
Абсолютный прирост (у)· |
yбi = yi - yo |
yцi = yi - yi-1 |
Коэффициент роста (Кр) |
|
|
Темп роста** (Тр) |
|
|
Коэффициент прироста (Кпр) |
|
|
Темп прироста (Тпр) |
Тпрбi=Кпрбi·100 Тпрбi=Трбi-100 |
Тпрцi=Кпрцi·100 Тпрцi=Трцi-100 |
Абсолютное значение одного процента прироста (А) |
- |
|
* Между базисными и цепными абсолютными приростами существует взаимосвязь: сумма цепных абсолютных приростов уц равна базисному абсолютному приросту последнего периода ряда динамики убn . ** Между базисными и цепными коэффициентами роста имеется связь: произведение последовательных цепных коэффициентов роста равна базисному коэффициенту роста, а частное от деления последующего базисного коэффициента роста на предыдущий равно соответствующему цепному коэффициенту.
Для иллюстрации расчетов приведенных статистических показателей рассмотрим следующий ряд динамики в табл. 8
Таблица 8 - Динамика производства обуви в РФ за 1992-1997 гг.
Год |
Млн.пар |
Абсолютный прирост, млн. пар |
Темпы роста, % |
Темпы прироста, % |
Абсолютное значение 1% прироста, млн.пар |
|||
Базисный |
цепной |
базисный |
цепной |
базисный |
цепной |
|||
1992 |
220 |
- |
- |
100,0 |
- |
- |
- |
- |
1993 |
146 |
-74 |
-74 |
66,4 |
66,4 |
-33,6 |
-33,6 |
2,20 |
1994 |
77 |
-143 |
-69 |
35,0 |
52,7 |
-65,0 |
-47,3 |
1,46 |
1995 |
53 |
-167 |
-24 |
24,1 |
68,8 |
-75,9 |
-31,2 |
0,77 |
1996 |
32 |
-188 |
-21 |
14,5 |
60,4 |
-83,5 |
-39,6 |
0,53 |
1997 |
31 |
-189 |
-1 |
14,1 |
96,9 |
-85,9 |
-3,1 |
0,32 |


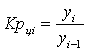

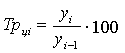
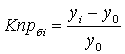 Knpбi=Kpбi-1
Knpбi=Kpбi-1
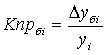
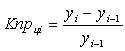 Knpцi=Kpцi-1
Knpцi=Kpцi-1